Слайд 2
Цели:
Способствовать формированию представления об истории возникновения и эволюции
логического мышления.
Способствовать формированию навыков формально-логического мышления, умению рассуждать,
формулировать выводы с использованием рефлексии.
Создать условия для формирования знаний и навыков о возможности однозначной интерпретации произвольной информации на основе алгебры логики.
Способствовать формированию информацион-ной культуры и потребности в приобретении знаний.
Слайд 3
Персоналии.
Основы формальной логики заложил ученый Древней Греции
–Аристотель.
Заслуга ученого состоит в том, что он отделил форму
мышления от содержания, попытался соединить логику и математику, разработал раздел теории доказательств.
Аристотель.
(384 г.-322 г. до н.э.)
Слайд 4
Персоналии.
Лейбниц взглянул на логику Аристотеля через призму математики.
Им написан трактат - «Азбука мыслей», сжатый и краткий
язык символов.
Лейбниц разработал идею логического исчисления. Рассуждения обозначил буквами, сложные выска-зывания - формулами.
В результате удалось содержательные рассужде-ния заменить формальны-ми вычислениями.
ВИЛЬГЕЛЬМ ЛЕЙБНИЦ
(1646-1716)
Слайд 5
Персоналии.
Дж.Буль - автор извест-ных произведений, в
т.ч. работы «Математический анализ логики»(1847г.)
Основной труд Дж. Буля -
«Исследование законов мысли», в котором представлен раздел логики - алгебра высказываний.
Джордж Буль
1815 – 1864 г.г.
Слайд 6
ЛОГИКА– это наука о формах и способах мышления
АЛГЕБРА ЛОГИКИ – раздел математической логики, изучающий высказывания и
операции над ними.
Слайд 7
ПОНЯТИЕ – это форма мышления, фиксирующая основные, существенные
признаки объекта.
Понятие имеет две стороны: содержание и
объем.
Содержание - это совокупность признаков объекта.
Объем – это совокупность (количество) объектов на которые эти признаки распространяются.
Слайд 8
ВЫСКАЗЫВАНИЕ – это форма мышления, в которой что-либо
утверждается или отрицается о свойствах реальных предметов и отношениях
между ними. Высказывание может быть истинно или ложно.
Свое понимание окружающего мира человек формулирует в форме высказываний.(суждений, утверждений). Высказывание строиться на основе понятий и по форме является повествовательным предложением. Высказывание об объекте может быть истинным или ложным, но не может быть истинным и ложным одновременно.
Высказывание не может быть вопросительным или повелительным т.к. оценка истинности или ложности невозможна. Истинность является величиной относительной, и завесит от многих причин и обстоятельств.
Слайд 9
УМОЗАКЛЮЧЕНИЕ – это форма мышления, с помощью которой
из одного или нескольких суждений может быть получено новое
суждение (заключение).
Умозаключение позволяет на основе известных фактов, выраженных в форме высказываний, получить заключение, т.е. новое знание.
Посылками умозаключения могут быть только истинные суждения, тогда заключение будет истинным, в противном случае можно прийти к ложному умозаключению.
Слайд 10
Основные понятия
Константы алгебры логики
(булевой алгебры) – логический 0 (ложь) и логическая 1
(истина).
Логические переменные принимают только два значения - логический 0 или логическая 1.
Слайд 11
Логической функцией F от набора логических переменных х1,х2,…,хn
называется функция, которая может принимать только два значения: логический
0 или логическая 1.
Любая логическая функция может быть задана с помощью таблицы истинности.
Слайд 12
Проверь себя:
1 Каково определение формы понятие.
2 Назовите основные характеристики понятия?
3 Приведите
примеры понятий.
4 Определение высказывания.
5 Какие значения принимает высказывание ?
6 Может ли суждение,
высказанное в повелительной форме являться высказыванием?
7 Придумайте и запишите в тетрадь простые высказывания.
8 Придумайте и запишите в тетрадь сложные высказывания.
Слайд 13
Элементарные логические операции.
Таблицы истинности.
Логические схемы.
Слайд 14
Основные логические операции:
Конъюнкция, логическое умножение (and - и);
Дизъюнкция,
логическое сложение (or - или);
Инверсия, логическое отрицание (not -
не);
Импликация ( - следование)(если высказывание истинно, то…)
Эквивалентность (~ - тогда и только тогда, когда)
Высказывания в алгебре логики обозначаются латинскими буквами
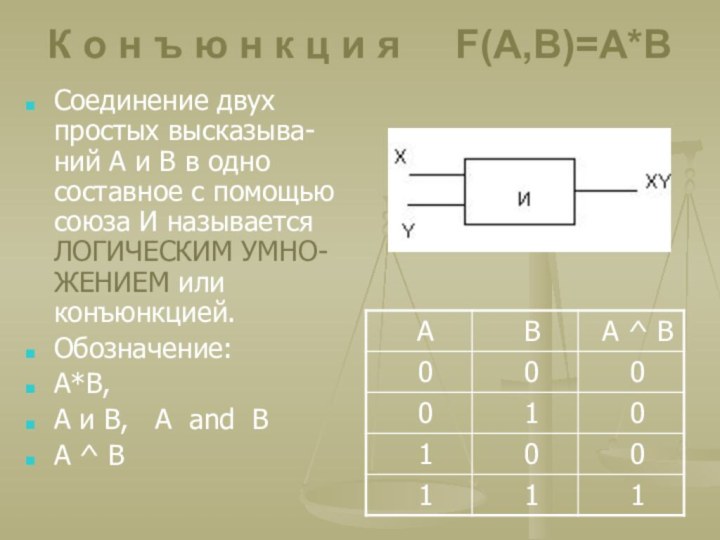
и я F(A,B)=A*B
Соединение двух простых высказыва-ний А
и В в одно составное с помощью союза И называется ЛОГИЧЕСКИМ УМНО-ЖЕНИЕМ или конъюнкцией.
Обозначение:
А*В,
А и В, А and В
А ^ В
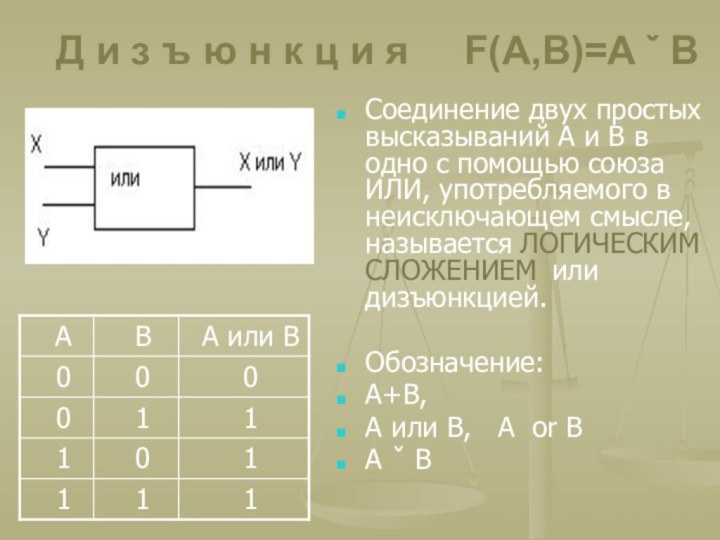
и я F(A,B)=A ˇ B
Соединение двух простых
высказываний А и В в одно с помощью союза ИЛИ, употребляемого в неисключающем смысле, называется ЛОГИЧЕСКИМ СЛОЖЕНИЕМ или дизъюнкцией.
Обозначение:
А+В,
А или В, А or В
А ˇ В
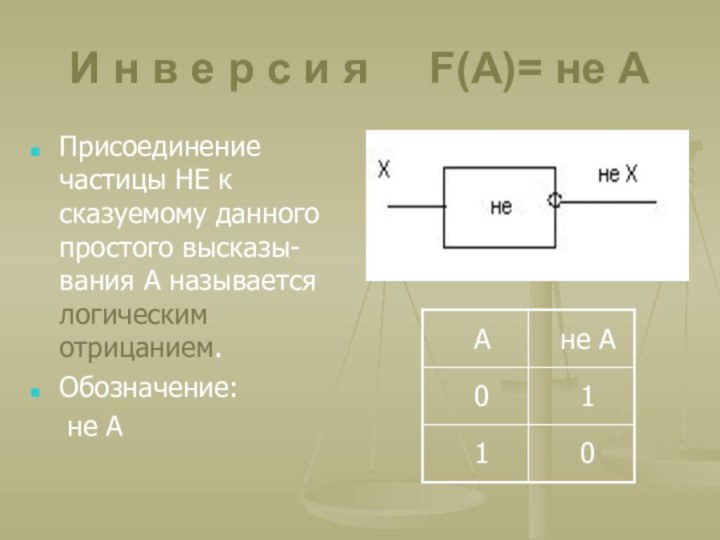
F(A)= не A
Присоединение частицы НЕ к сказуемому
данного простого высказы-вания А называется логическим отрицанием.
Обозначение:
не А
Слайд 18
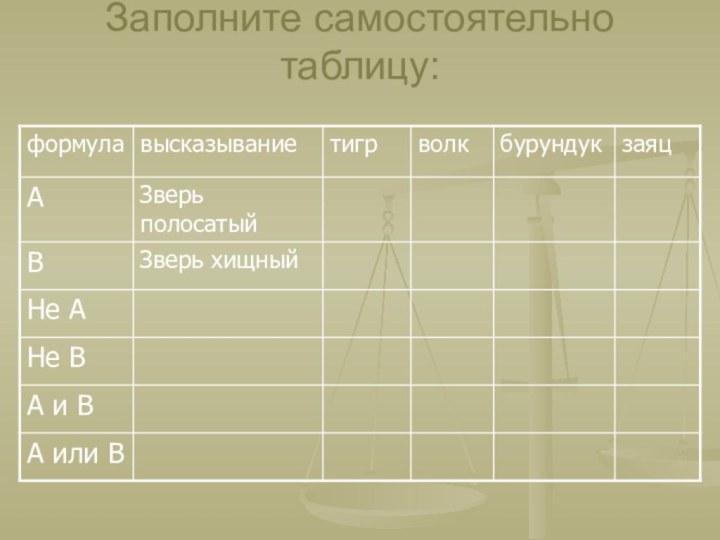
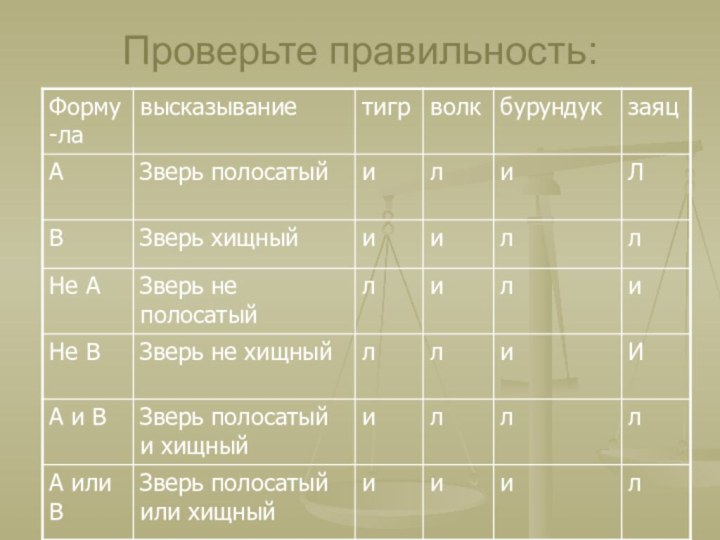
Заполните самостоятельно таблицу:
Слайд 20
Импликация F(A,B)= A → B
Импликацией двух высказываний А
и В называется новое высказывание, которое ложно только тогда,
когда высказывание А истинно, а В – ложно, во всех же остальных случаях истинно.
Обозначение:
А → В
А следует В
Слайд 21
Эквивалентность F(A,B)= A ~ B
Соединение двух простых высказываний
А и В в одно с помощью связки «…тогда
и только тогда, когда…» , называется операцией эквивалентности.
Обозначение:
А ~ В
Слайд 23
Логические (булевы) выражения -
Это булевы
константы и переменные, связанные логическими операциями И, ИЛИ и
НЕ в единую формулу.
СТАРШИНСТВО ЛОГИЧЕСКИХ ОПЕРАЦИЙ :
Инверсия
Конъюнкция
Дизъюнкция
Для изменения порядка действий
используются скобки.
Слайд 24
Теоремы алгебры логики
1. не 0 = 1,
не 1 = 0
2. Х or 0=Х,
Х · 1=Х
3. Х or 1=1, Х · 0=0
4. Х or Х=Х, Х · Х=Х – з-н идемпотентности -
основной закон алгебры Буля, в соответствии с
которым исключаются все коэффициенты и
показатели степеней.
А+А+А+А=А
А·А·А=А
Слайд 25
Теоремы алгебры логики
5. Х or неХ=1, Х ·
неХ=0
6. не(неХ) = Х – закон двойного
отрицания
7. Х or Y = Y or X, X · Y = Y · X
коммутативный закон
8. X or X · Y=X, X ·(X or Y)=X - закон
поглощения
Слайд 26
Теоремы алгебры логики
Для самостоятельного изучения:
Закон де Моргана
не (А
или В) = (не А) и (не В)
не
(А и В) = (не А) или (не В)
Ассоциативный закон
Сочетательный (ассоциативный) закон:
(А или В) или С = А или (В или С)
(А и В) и С = А и (В и С)
Дистрибутивный закон
Распределительный (дистрибутивный) закон:
(А и В) или С = (А или С) и (В или С)
(А или В) и С = (А и С) или (А и В)
Слайд 27
Алгоритмы решения логических задач:
Большинство логических задач
решается по следующему алгоритму:
изучение условия задачи
обозначение используемых высказываний буквами
составление
логических выражений, удовлетворяющих всем требованиям задачи
объединение их в одно выражение
Вычисление всех значений этого логического выражения
проверка полученного решения по условию задачи
Слайд 28
Используемая литература:
Информатика.Толковый словарь основных терминов. – Тула:Арктоус, 1996
Касаткин
ВН, Информация. Алгоритмы.– Москва:Просвещение,1991
Шауцукова ,Информатика.-М.: Просвещение,2001
Информатика. Задачник-практикум в 2
т. /Под ред ИГ Семакина, ЕК Хеннера- М.:ЛБЗ, 2000