Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему по информатике Методика обучения теме Логика в профильном курсе. Решение задач ЕГЭ 17, 18

Содержание

2. Что нужно знать?
7. Решение задач
8. 1) Формулировка задачи: Элементами множества А
9. Решение:Введем обозначения:P ≡ (x Î {2, 4,
11. 2) Формулировка задачи: Элементами множества А
12. Решение:Введем обозначения:P ≡ (x Î {2, 4,
14. 3) Формулировка задачи: Сколько различных решений
15. Решение:Дизъюнкция истинна, когда хотя бы одно из
16. Значит, для выражения (K  L 
17. Складывая все полученные результаты, получаем 2+2=4. Ответ: уравнение имеет 4 решения
18. 4) Формулировка задачи: Обозначим через ДЕЛ(n,
19. Решение:Введём обозначения: A = ДЕЛ(x, А), D14 = ДЕЛ(x, 14), D21 = ДЕЛ(x, 21).Введём множества:A — множество натуральных
20. Исходное выражение принимает вид:А (D14  D21)
21. Порядок заполнения таблицы:Заполняем значения х, входящие в
22. По условию задачи необходимо найти наименьшее натуральное
23. 4) Формулировка задачи: Введём выражение M
24. Решение:Упростим выражение (заменим импликации дизъюнкциями):(X & 102
25. Рассмотрим первой выражение (X & 102 =
26. Проанализируем поразрядную конъюнкцию числа 11001102 с числом
27. Рассмотрим второе выражение (X & 36 0)Только
28. Проанализируем поразрядную конъюнкцию числа 1001002 с числом
29. Скачать презентацию
30. Похожие презентации

Что нужно знать?

Главная
Информатика
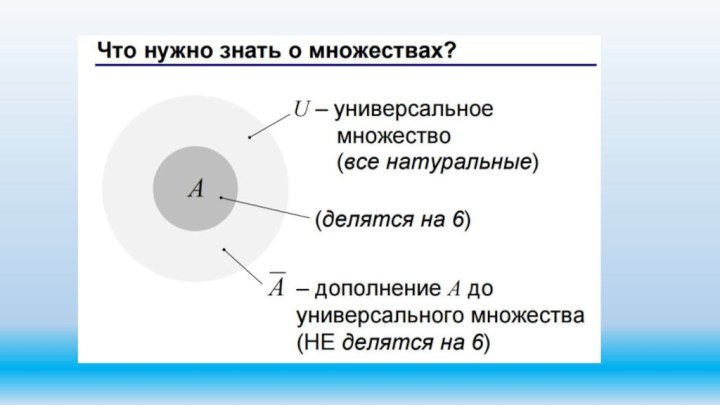
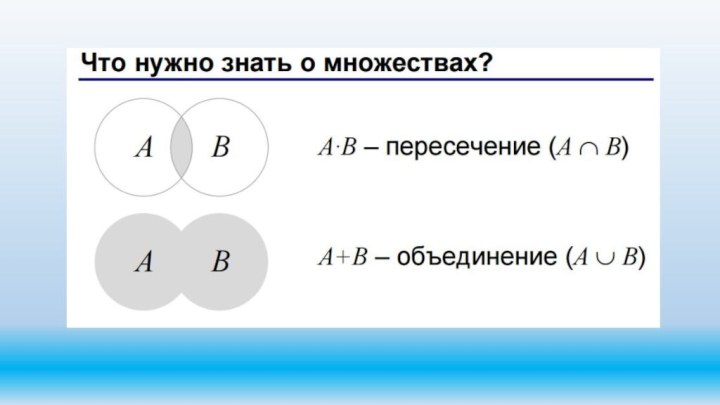
Презентация по информатике Методика обучения теме Логика в профильном курсе. Решение задач ЕГЭ 17, 18

Методика обучения теме «Логика» в профильном курсе. Решение задач ЕГЭ 17, 18Коровина Е.А.

Презентация по информатике Методика обучения теме Логика в профильном курсе. Решение задач ЕГЭ 17, 18

1) Формулировка задачи: Элементами множества А являются натуральные числа. Известно, что

Решение:Введем обозначения:P ≡ (x Î {2, 4, 6, 8, 10, 12});Q ≡

2) Формулировка задачи: Элементами множества А являются натуральные числа. Известно, что

3) Формулировка задачи: Сколько различных решений имеет уравнение (K  L

Решение:Дизъюнкция истинна, когда хотя бы одно из выражений истинно.(K  L 

Значит, для выражения (K  L  M) = 1 существует единственный

Складывая все полученные результаты, получаем 2+2=4. Ответ: уравнение имеет 4 решения

4) Формулировка задачи: Обозначим через ДЕЛ(n, m) утверждение «натуральное число n

Решение:Введём обозначения: A = ДЕЛ(x, А), D14 = ДЕЛ(x, 14), D21 = ДЕЛ(x, 21).Введём множества:A — множество натуральных чисел, для которых выполняется условие A,D14 —

Исходное выражение принимает вид:А (D14  D21) = 1.Преобразуем данное выражение:А (D14

Порядок заполнения таблицы:Заполняем значения х, входящие в состав множеств D14 и D21

По условию задачи необходимо найти наименьшее натуральное число из множества А, значит,

4) Формулировка задачи: Введём выражение M & K, обозначающее поразрядную конъюнкцию

Решение:Упростим выражение (заменим импликации дизъюнкциями):(X & 102 0)  ((X & 36

Рассмотрим первой выражение (X & 102 = 0):Найдем все значения х, при

Проанализируем поразрядную конъюнкцию числа 11001102 с числом Х2Вывод: выражение не получит истину

Рассмотрим второе выражение (X & 36 0)Только для 1, 2, 5 и

Проанализируем поразрядную конъюнкцию числа 1001002 с числом Х2Вывод: выражение не получит истину

Все неучтенные биты нужно добавить в третье логическое выражение (X & A

Слайды презентации

Слайд 2 Что нужно знать?

Слайд 7 Решение задач

Слайд 8 1) Формулировка задачи: Элементами множества А являются натуральные

числа. Известно, что выражение (x Î {2, 4, 6, 8,

10, 12}) → (((x Î {3, 6, 9, 12, 15})   ¬(x Î A)) → ¬(x Î {2, 4, 6, 8, 10, 12})) истинно (т. е. принимает значение 1) при любом значении переменной х. Определите наименьшее возможное значение суммы элементов множества A.

Слайд 9 Решение:
Введем обозначения:
P ≡ (x Î {2, 4, 6,

8, 10, 12});
Q ≡ (x Î {3, 6, 9,

12, 15}) ;
A ≡ (x Î A).
Преобразовав исходное выражение, получаем:
P → ((Q  ¬A) → ¬P)= P → (¬(Q  ¬A)  ¬P)=
=P → (¬ Q  A  ¬P)= ¬ P  ¬ Q  A  ¬P= ¬ P  ¬ Q  A

Слайд 10

Слайд 11 2) Формулировка задачи: Элементами множества А являются натуральные

числа. Известно, что выражение ¬(x Î {2, 4, 6, 8,

10, 12})  (¬(x Î {3, 6, 9, 12, 15}) → (x Î A)) истинно (т. е. принимает значение 1) при любом значении переменной х. Определите наименьшее возможное значение произведения элементов множества A.

Слайд 12 Решение:
Введем обозначения:
P ≡ (x Î {2, 4, 6,

Решение:Введем обозначения:P ≡ (x Î {2, 4, 6, 8, 10, 12})

8, 10, 12}) ;
Q ≡ (x Î {3, 6,

9, 12, 15}) ;
A ≡ (x Î A).
Преобразовав исходное выражение, получаем:
¬ P  (¬ Q → A) = ¬ P  Q  A = 1

Слайд 13

Слайд 14 3) Формулировка задачи: Сколько различных решений имеет уравнение (K

 L  M)  (¬L  ¬M 

N) = 1 где K, L, M, N – логические переменные? В ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.

Слайд 15 Решение:
Дизъюнкция истинна, когда хотя бы одно из выражений

истинно.
(K  L  M) = 1 или (¬L

 ¬M  N) = 1
Логические переменные L и M являются зависимыми друг от друга, переменные K и N – независимы.
Каждое выражение является конъюнкцией логических переменных и истинно, только в том случае, когда истинны все высказывания, входящие в данное выражение.

Слайд 16 Значит, для выражения (K  L  M)

Значит, для выражения (K  L  M) = 1 существует

= 1 существует единственный вариант решения, когда K=1, L=1,

M=1, но независимая переменная N может принимать любое значение (либо 1, либо 0), следовательно вариантов решения уже 1*2=2.
Подобным образом находим варианты решения выражения (¬L  ¬M  N) = 1, учитывая, что переменная K тоже независима и может принимать любое значение. Получаем тоже 2 варианта решения.

Слайд 17 Складывая все полученные результаты, получаем 2+2=4.
Ответ: уравнение

имеет 4 решения

Слайд 18 4) Формулировка задачи: Обозначим через ДЕЛ(n, m) утверждение

«натуральное число n делится без остатка на натуральное число

m». Для какого наименьшего натурального числа А формула ДЕЛ(x, A)  (ДЕЛ(x, 14)  ДЕЛ(x, 21)) тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

Слайд 19 Решение:
Введём обозначения:
A = ДЕЛ(x, А),
D14 = ДЕЛ(x, 14),
D21 = ДЕЛ(x, 21).
Введём множества:
A — множество натуральных чисел,

Решение:Введём обозначения: A = ДЕЛ(x, А), D14 = ДЕЛ(x, 14), D21 = ДЕЛ(x, 21).Введём множества:A — множество натуральных чисел, для которых выполняется

для которых выполняется условие A,
D14 — множество натуральных чисел, для которых

выполняется условие D14,
D21 — множество натуральных чисел, для которых выполняется условие D21.

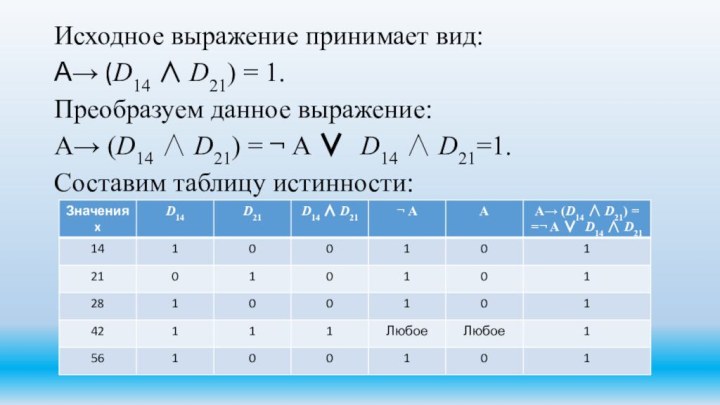
Слайд 20 Исходное выражение принимает вид:
А (D14  D21) =

Исходное выражение принимает вид:А (D14  D21) = 1.Преобразуем данное выражение:А

1.
Преобразуем данное выражение:
А (D14  D21) = ¬ А

 D14  D21=1.
Составим таблицу истинности:

Слайд 21 Порядок заполнения таблицы:
Заполняем значения х, входящие в состав

Порядок заполнения таблицы:Заполняем значения х, входящие в состав множеств D14 и

множеств D14 и D21 ,
заполняем значения логического выражения

(D14  D21 ),
заполняем единицами значения выражения А (D14  D21) = ¬ А  D14  D21, т.к. по условию дано, что это выражение истинно,
Заполняем значения ¬ А,
Заполняем значения А.

Слайд 22 По условию задачи необходимо найти наименьшее натуральное число

По условию задачи необходимо найти наименьшее натуральное число из множества А,

из множества А, значит, выбираем первый вариант решения, где

значение А может быть любым. В данном случае, это число 42.
Ответ: 42

Слайд 23 4) Формулировка задачи: Введём выражение M & K,

обозначающее поразрядную конъюнкцию M и K (логическое «И» между

соответствующими битами двоичной записи). Определите наименьшее натуральное число A, такое что выражение (X & 102 <> 0)  ((X & 36 = 0)  (X & A <> 0)) тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной X)?

Слайд 24 Решение:
Упростим выражение (заменим импликации дизъюнкциями):
(X & 102

Решение:Упростим выражение (заменим импликации дизъюнкциями):(X & 102 0)  ((X &

0)  ((X & 36 = 0)  (X

& A <> 0)) =
= (X & 102 <> 0)  ((X & 36 <> 0)  (X & A <> 0)) =
= (X & 102 = 0)  ((X & 36 <> 0)  (X & A <> 0)) =
= (X & 102 = 0)  (X & 36 <> 0)  (X & A <> 0).
Для того, чтобы выражение
(X & 102 = 0)  (X & 36 <> 0)  (X & A <> 0)
было истинно достаточно, чтобы хотя бы одно из логических выражений было истинно.