- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по теме Алгебра логики
Содержание
- 2. ЛОГИКА – это наука о формах и способах мышления. Учение о способах рассуждений и доказательств.
- 3. ПОНЯТИЕ – это форма мышления, которая выделяет
- 4. ВЫСКАЗЫВАНИЕ – это повествовательное предложение, относительно которого
- 5. Задание 1. Какие из предложений являются высказываниями.
- 6. АЛГЕБРА – это наука об общих операциях,
- 7. Простые высказывания в алгебре логики обозначаются заглавными
- 8. Составные высказывания на естественном языке образуются с
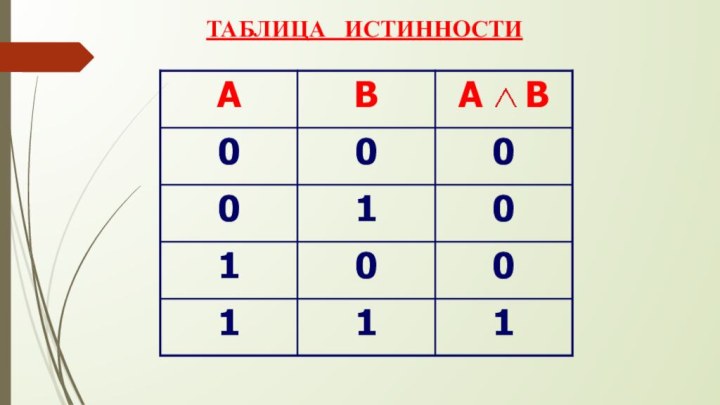
- 9. ОПЕРАЦИИ АЛГЕБРЫ ЛОГИКИКОНЪЮНКЦИЯ (логическое умножение) – (соответствует
- 10. ТАБЛИЦА ИСТИННОСТИ
- 11. ДИЗЪЮНКЦИЯ (логическое сложение) (соответствует союзу ИЛИ; обозначается
- 12. ТАБЛИЦА ИСТИННОСТИ
- 13. ИНВЕРСИЯ (логическое отрицание) (соответствует частице НЕ; обозначается
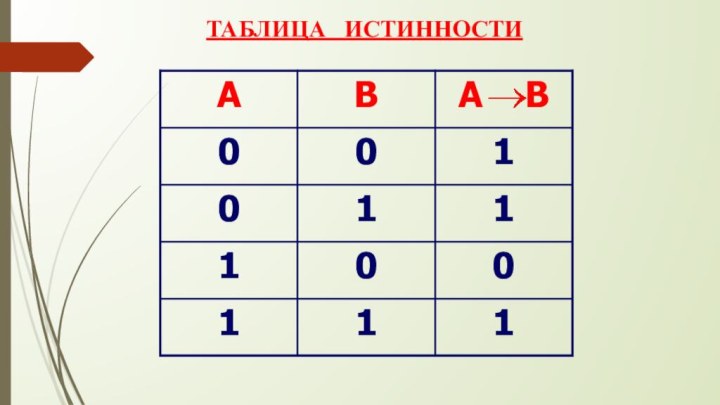
- 14. ИМПЛИКАЦИЯ (логическое следование) (в естественном языке соответствует
- 15. ТАБЛИЦА ИСТИННОСТИ
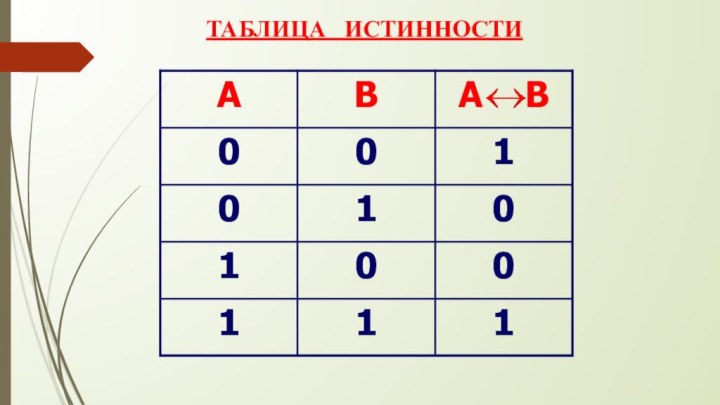
- 16. ЭКВИВАЛЕНЦИЯ (равнозначность) (в естественном языке соответствует обороту
- 17. ТАБЛИЦА ИСТИННОСТИ
- 18. Логические операции имеют следующий приоритет: ДЕЙСТВИЯ В СКОБКАХ ИНВЕРСИЯ КОНЪЮНКЦИЯ ДИЗЪЮНКЦИЯ ИМПЛИКАЦИЯ ЭКВИВАЛЕНЦИЯ
- 19. ЗАДАНИЕ 2. Определите истинность составного высказывания
- 20. ЗАДАНИЕ 3. Какие из высказываний A, B,
- 21. ЛОГИЧЕСКИЕВЫРАЖЕНИЯИТАБЛИЦЫИСТИННОСТИ
- 22. Таблицу, показывающую, какие значения принимает составное высказывание
- 23. АЛГОРИТМ ПОСТРОЕНИЯ ТАБЛИЦЫ ИСТИННОСТИ: 1. Подсчитать количество
- 24. 4. Определить количество столбцов в таблице: число
- 25. ЗАПОЛНЕНИЕ НАБОРОВ ВХОДНЫХ ПЕРЕМЕННЫХ: 1. Определить количество
- 26. 3. Разделить колонку значений второй переменной на
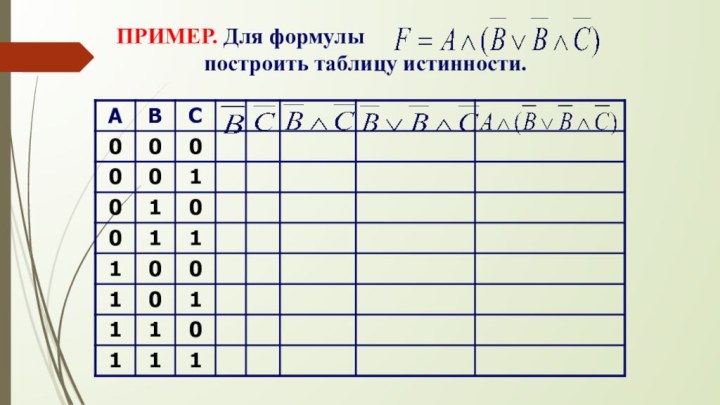
- 27. ПРИМЕР. Для формулыпостроить таблицу истинности.
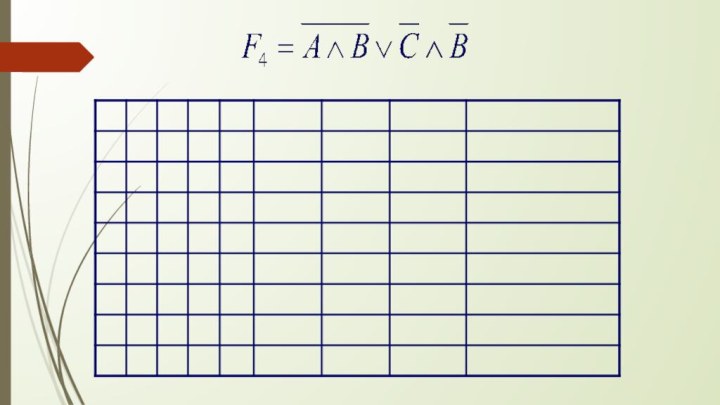
- 28. Задание 10. Для следующих логических формул построить таблицы истинности.
- 31. Задание 11. Докажите справедливость следующих тождеств, построив таблицы истинности
- 35. ПОСТРОЕНИЕТАБЛИЦИСТИННОСТИ
- 36. Задание 12. Определите, при каких значениях A, B и C следующие высказывания истинны
- 40. РЕШЕНИЕЛОГИЧЕСКИХЗАДАЧ
- 41. Задача 1. В одной стране жили рыцари,
- 42. Решение с помощью таблицы А сказал: Я
- 43. Задача 2. После традиционного вечера встречи с
- 45. Задача 3. В конструкторском бюро работают Антонов,
- 47. Задача 4. В одном доме живут Воронов,
- 49. Задача 5. В классе 36 человек. Ученики
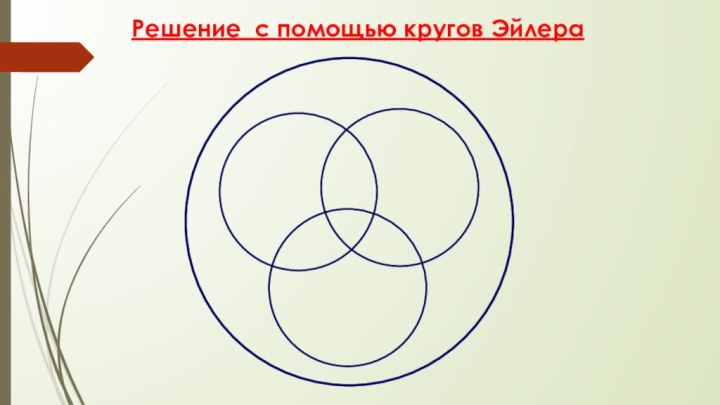
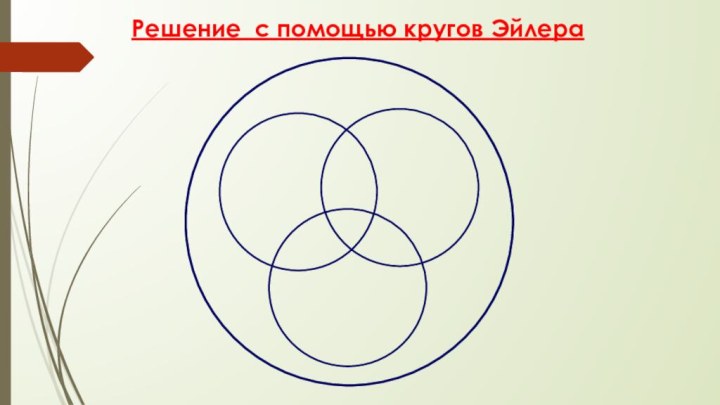
- 50. Решение с помощью кругов Эйлера
- 51. Задача 6. После зимних каникул классный руководитель
- 52. Решение с помощью кругов Эйлера
- 53. ЛОГИЧЕСКИЕОСНОВЫУСТРОЙСТВАКОМПЬЮТЕРА
- 54. Логические элементы – это электронные схемы с
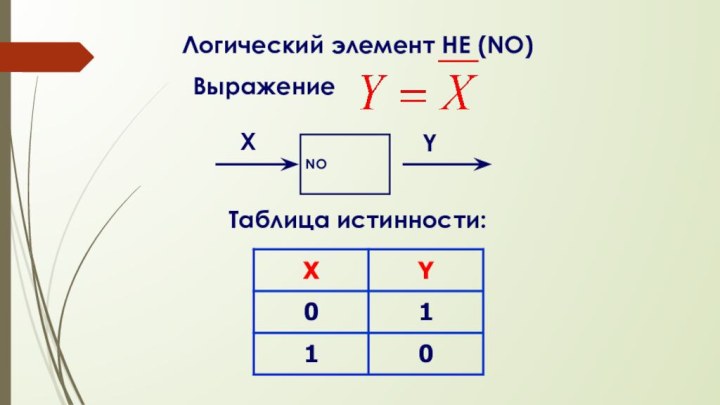
- 55. Логический элемент НЕ (NO) Выражение NOХYТаблица истинности:
- 56. Логический элемент И (AND) Выражение ANDХZТаблица истинности:Y
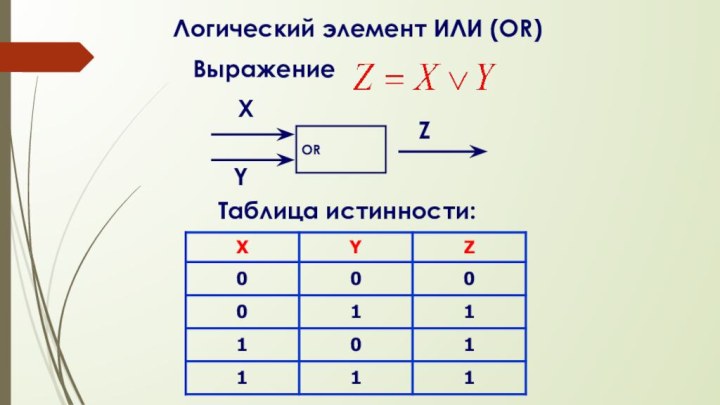
- 57. Логический элемент ИЛИ (OR) Выражение ORХZТаблица истинности:Y
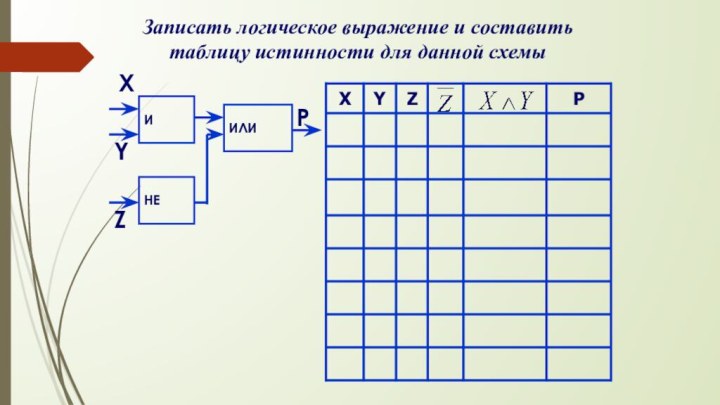
- 58. ZЗаписать логическое выражение и составить таблицу истинности для данной схемы ИХPYНЕИЛИ
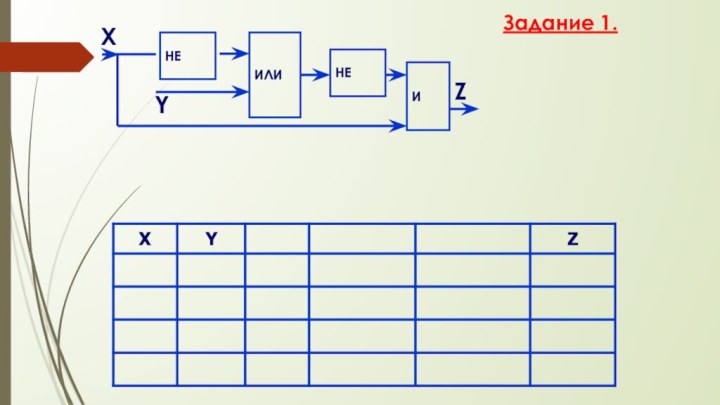
- 59. Задание 1. НЕХYИЛИZИНЕ
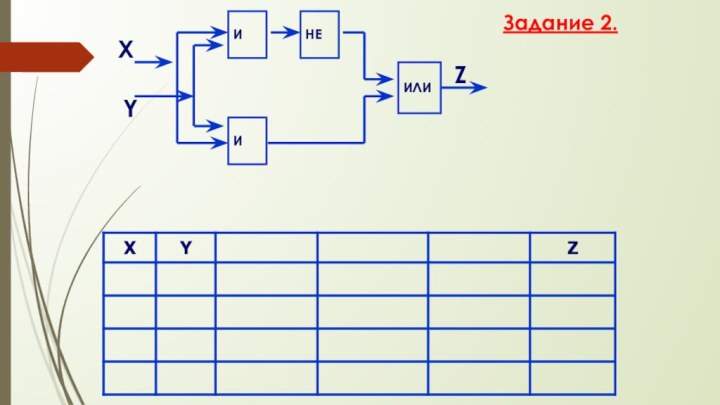
- 60. ZИХYИЛИНЕИЗадание 2.
- 61. НЕХYZИЛИИИНЕЗадание 3.
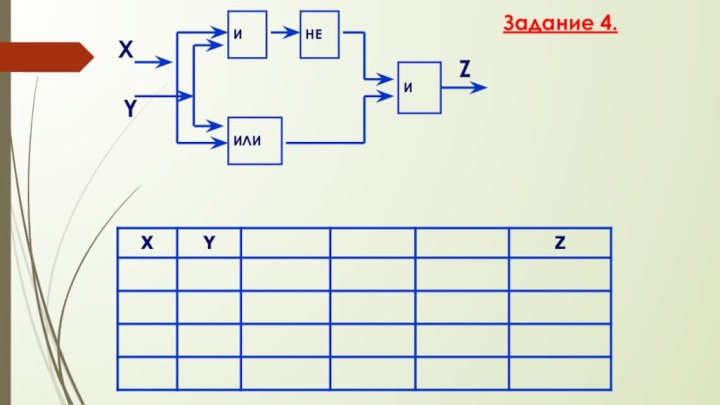
- 62. ZИХYИНЕИЛИЗадание 4.
- 63. ZИХYИЛИНЕИЛИЗадание 5.
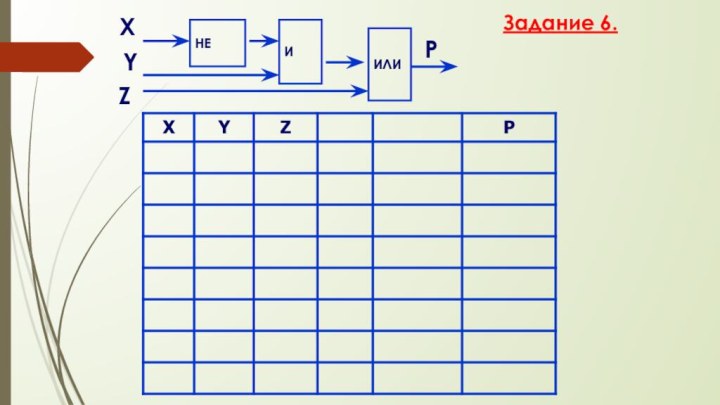
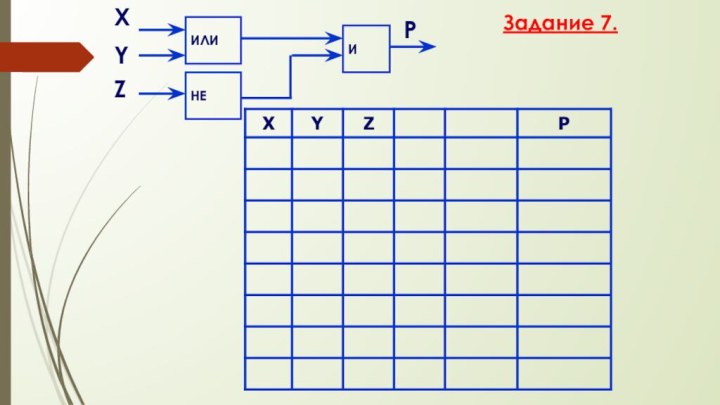
- 64. НЕХPYИZИЛИЗадание 6.
- 65. Скачать презентацию
- 66. Похожие презентации
ЛОГИКА – это наука о формах и способах мышления. Учение о способах рассуждений и доказательств.

























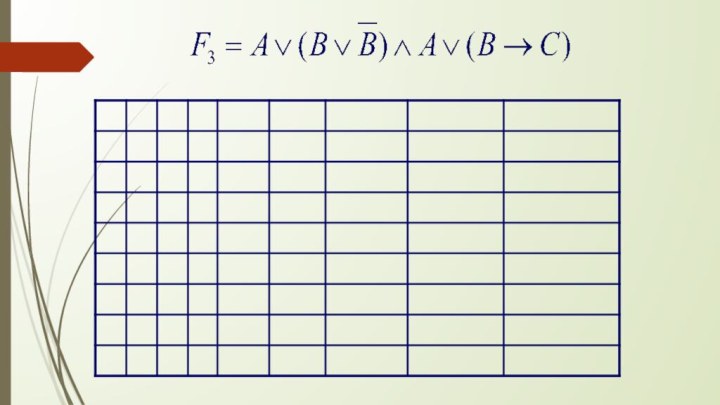




















Слайд 2
ЛОГИКА –
это наука о формах и способах
мышления. Учение о способах рассуждений и доказательств.
Слайд 3 ПОНЯТИЕ – это форма мышления, которая выделяет существенные
признаки предмета, позволяющие отличать его от других, например, ПРЯМОУГОЛЬНИК,
КОМПЬЮТЕРМЫШЛЕНИЕ
осуществляется через:
ВЫСКАЗЫВАНИЕ – это формулировка своего понимания окружающего мира.
УМОЗАКЛЮЧЕНИЕ – это форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое (знание или вывод).
Слайд 4 ВЫСКАЗЫВАНИЕ – это повествовательное предложение, относительно которого можно
сказать, истинно оно или ложно
ПРИМЕР
«Буква «а» - гласная»
-истинное высказывание.
«Компьютер был изобретен в XXI веке» - ложное высказывание.
Слайд 5 Задание 1. Какие из предложений являются высказываниями. Определите
их истинность.
Какой длины эта лента?
2. Прослушайте сообщение.
3. Делайте
утреннюю зарядку!4. Назовите устройство ввода информации.
5. Кто отсутствует на уроке?
6. Париж – столица Англии.
7. Число 11 является простым.
8. 4 + 5 = 10.
9. Без труда не вытащишь и рыбку из пруда.
10. Сложите числа 2 и 5.
11. Некоторые медведи живут на севере.
12. Все медведи – бурые.
Слайд 6 АЛГЕБРА – это наука об общих операциях, аналогичных
сложению и умножению, которые могут выполняться над различными математическими
объектами.АЛГЕБРА ЛОГИКИ выполняет различные операции над высказываниями.
ВЫСКАЗЫВАНИЯ могут быть ПРОСТЫМИ и СОСТАВНЫМИ
Слайд 7 Простые высказывания в алгебре логики обозначаются заглавными латинскими
буквами:
A = {Два больше трех}
В = {На яблонях не
растут бананы}Истинному высказыванию ставится в соответствие 1, ложному – 0.
Таким образом, А = 0, В = 1.
Слайд 8 Составные высказывания на естественном языке образуются с помощью
союзов:
Летом Саша поедет в деревню и, если будет хорошая
погода, то он пойдет на рыбалку.Можно разбить на простые высказывания:
A = {Саша поедет в деревню}
В = {Будет хорошая погода}
С = {Он пойдет на рыбалку}
В алгебре логики союзы заменяются на логические операции
Слайд 9
ОПЕРАЦИИ АЛГЕБРЫ ЛОГИКИ
КОНЪЮНКЦИЯ
(логическое умножение) –
(соответствует союзу
И;
обозначается )
это логическая операция, которая
двум простым высказываниям ставит в соответствие составное истинное тогда и только тогда, когда оба простых высказывания истинны.
Слайд 11
ДИЗЪЮНКЦИЯ (логическое сложение)
(соответствует союзу ИЛИ;
обозначается
)
это логическая операция, которая двум простым высказываниям
ставит в соответствие составное ложное тогда и только тогда, когда оба простых высказывания ложны.
Слайд 13
ИНВЕРСИЯ (логическое отрицание)
(соответствует частице НЕ;
обозначается
)
это логическая операция, которая истинное высказывание делает
ложным и, наоборот, ложное истинным. ТАБЛИЦА ИСТИННОСТИ
Слайд 14
ИМПЛИКАЦИЯ
(логическое следование)
(в естественном языке соответствует обороту
речи: ЕСЛИ…, ТО…;
обозначается )
это логическая
операция, которая двум простым высказываниям ставит в соответствие составное ложное тогда и только тогда, когда из истинного высказывания следует ложное.
Слайд 16
ЭКВИВАЛЕНЦИЯ (равнозначность)
(в естественном языке соответствует обороту речи:
ТОГДА И ТОЛЬКО ТОГДА;
В ТОМ И ТОЛЬКО В
ТОМ СЛУЧАЕ;обозначается )
это логическая операция, которая двум простым высказываниям ставит в соответствие составное истинное тогда и только тогда, когда оба исходных простых высказывания одновременно истинны или одновременно ложны.
Слайд 18
Логические операции имеют следующий приоритет:
ДЕЙСТВИЯ В СКОБКАХ
ИНВЕРСИЯ
КОНЪЮНКЦИЯ
ДИЗЪЮНКЦИЯ
ИМПЛИКАЦИЯ
ЭКВИВАЛЕНЦИЯ
Слайд 19
ЗАДАНИЕ 2. Определите истинность составного высказывания
,
состоящего из простых высказываний:
А={Принтер – устройство вывода информации},
В={Процессор – устройство хранения информации},
С={Монитор – устройство вывода информации},
D={Клавиатура – устройство обработки информации}.
Слайд 20 ЗАДАНИЕ 3. Какие из высказываний A, B, C
должны быть истинны и какие ложны, чтобы было ложно
логическое выражениеСлайд 22 Таблицу, показывающую, какие значения принимает составное высказывание при
всех сочетаниях (наборах) значений входящих в него простых высказываний,
называют ТАБЛИЦЕЙ ИСТИННОСТИ составного высказывания
Слайд 23
АЛГОРИТМ ПОСТРОЕНИЯ ТАБЛИЦЫ ИСТИННОСТИ:
1. Подсчитать количество простых
высказываний n в логическом выражении.
2. Определить число строк в
таблице m=2n.3. Установить последовательность логических операций с учетом скобок и приоритетов.
Слайд 24 4. Определить количество столбцов в таблице: число переменных
плюс число операций.
5. Выписать наборы входных переменных (используя
алгоритм).6. Провести заполнение таблицы истинности по столбикам, выполняя логические операции в соответствии с установленной последовательностью.
Слайд 25
ЗАПОЛНЕНИЕ НАБОРОВ ВХОДНЫХ ПЕРЕМЕННЫХ:
1. Определить количество наборов
входных переменных (оно соответствует числу строк в таблице и
определяется по формуле m=2n).2. Разделить колонку значений первой переменной пополам и заполнить верхнюю часть колонки 0, а нижнюю - 1.
Слайд 26 3. Разделить колонку значений второй переменной на четыре
части и заполнить каждую четверть чередующимися группами 0 и
1, начиная с группы 0.4. Продолжить деление колонок последующих переменных на 8, 16 и т. д. частей и заполнение их группами 0 и 1 до тех пор, пока группы 0 и 1 не будут состоять из одного символа.
Слайд 41 Задача 1. В одной стране жили рыцари, которые
всегда говорили только правду, и лжецы, которые всегда лгали.
Однажды в страну проник шпион по имени Мердок, который, как и всякий шпион, иногда говорил правду, иногда лгал, в зависимости от того, что ему выгодно. Шпион поселился с двумя жителями страны – рыцарем и лжецом. Всех троих арестовали в один день и привели на допрос. Никто не знал, кто из них кто. Они сделали следующие заявления:А сказал: Я – Мердок.
В сказал: А говорит правду.
С сказал: Я не мердок.
Кто же из них шпион – А, В или С?
Слайд 42
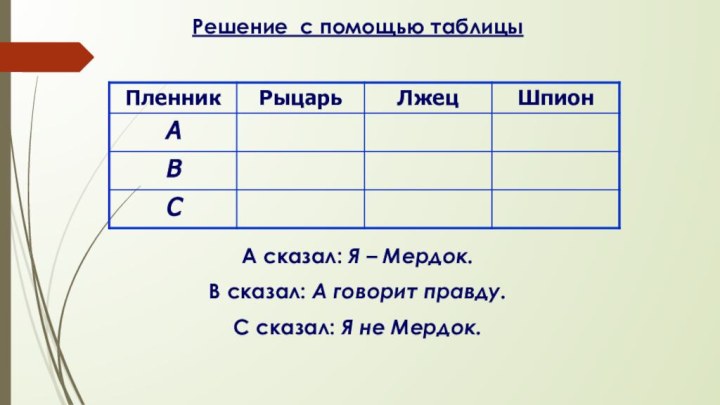
Решение с помощью таблицы
А сказал: Я –
Мердок.
В сказал: А говорит правду.
С сказал: Я не Мердок.
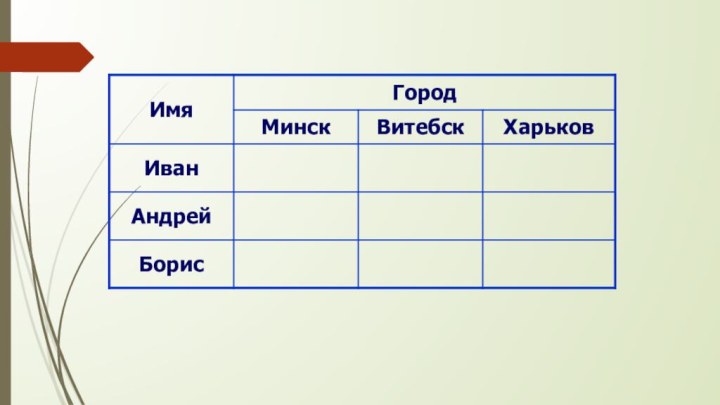
Слайд 43 Задача 2. После традиционного вечера встречи с выпускниками
школы в стенгазете появилась заметка о трех наших бывших
учениках. В ней было сказано, что Иван, Андрей и Борис стали учителями. Теперь они преподают разные дисциплины: один из них – математику, второй – физику, а третий – химию. Живут они тоже в разных городах: Минске, Витебске, Харькове. В заметке было также написано, что их первоначальные планы осуществились не полностью:1) Иван живет не Минске;
2) Андрей – не в Витебске;
3) Житель Минска преподает не математику;
4) Андрей преподает не физику;
5)Повезло только жителю Витебска: он преподает любимую химию.
Можно ли по этим данным определить кто где живет и что преподает?
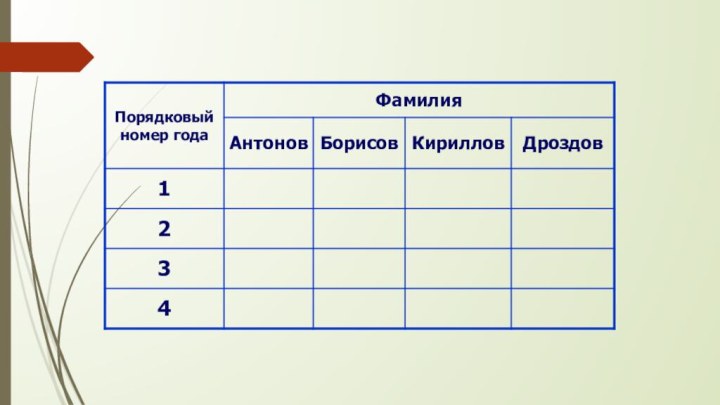
Слайд 45 Задача 3. В конструкторском бюро работают Антонов, Борисов
Кириллов и Дроздов. Все хотят отдыхать летом, и поэтому
при составлении графика отпусков всегда возникают споры. Попробуйте помочь составить график отпусков на 4 года, который бы удовлетворял следующим пожеланиям сотрудников:1) в отпуск сотрудники хотят идти только с мая по август;
2) продолжительность отпуска – один месяц;
3) в каждом месяце в отпуск может пойти только один человек;
4) за четыре года каждый из четырех сотрудников должен получить отпуск по одному разу в каждом из этих месяцев;
5) в первый год Кириллов хочет отдыхать в июле;
6) во второй год Антонову отпуск нужен в мае;
7) в третий год Дроздову отпуск нужен в июне;
8) Борисов на четвертый год предполагает уйти в отпуск в июле;
9) в августе все хотят отдыхать следующим образом: в первый год – Дроздов, во второй – Кириллов, в третий – Борисов, в четвертый – Антонов.
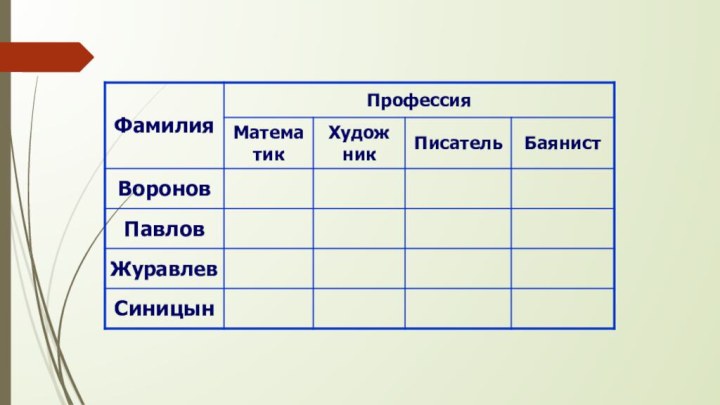
Слайд 47 Задача 4. В одном доме живут Воронов, Павлов,
Журавлев, Синицын. Один из них – математик, другой –
художник, третий – писатель, а четвертый – баянист. Известно, что:1) ни Воронов, ни Журавлев не умеют играть на баяне;
2) Журавлев не знаком с Вороновым;
3) писатель и художник в выходные уезжают на дачу к Павлову;
4) Писатель собирается написать очерк о Синицыне и Воронове;
Требуется определить кто есть кто.
Слайд 49 Задача 5. В классе 36 человек. Ученики этого
класса посещают математический, физический и химический кружки, причем математический
кружок посещают 18 человек, физический – 14, химический – 10. Кроме того, известно, что 2 человека посещают все три кружка, 8 человек – и математический и физический, 5 – и математический и химический, 3 – и физический и химическийСлайд 51 Задача 6. После зимних каникул классный руководитель спросил,
кто из ребят ходил в театр, кино или цирк.
Оказалось, что из 36 учеников класса двое не были ни в кино, ни в театре, ни в цирке. В кино побывало 25 человек, в театре – 11, в цирке – 17; и в кино, и в театре – 6; и в кино, и в цирке – 10; и в театре, и в цирке – 4.Сколько человек побывало и в кино, и в театре, и в цирке?
Слайд 54 Логические элементы – это электронные схемы с одним
или несколькими входами и одним выходом, через которые проходят
электрические сигналы, представляющие цифры 0 или 1.Принцип работы логических элементов наглядно изображает таблица истинности