- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Алгебра логики
Содержание
- 2. Еще живший в 384 - 322 г.г.
- 3. Немецкий ученый и философ Готфрид - Вильгельм
- 4. Claude Elwood Shannon (1916 - 2001). Является
- 5. Буль (Boole) Джордж (1815 — 1864) английский
- 6. Алгебра в широком смысле этого слова –
- 7. Логика – это наука о формах и способах мышленияФормы мышленияпонятиесуждение(высказывание, утверждение)умозаключение
- 8. Понятие - это форма мышления, которая выделяет существенные
- 9. Суждения - это форма мышления, в которой утверждается
- 10. Какие из предложений являются высказываниями? Определите их
- 11. Какие из предложений являются высказываниями? Определите их
- 12. МОУ "Экономическая гимназия" Никифорова Л.Г, Пример 1:заключение
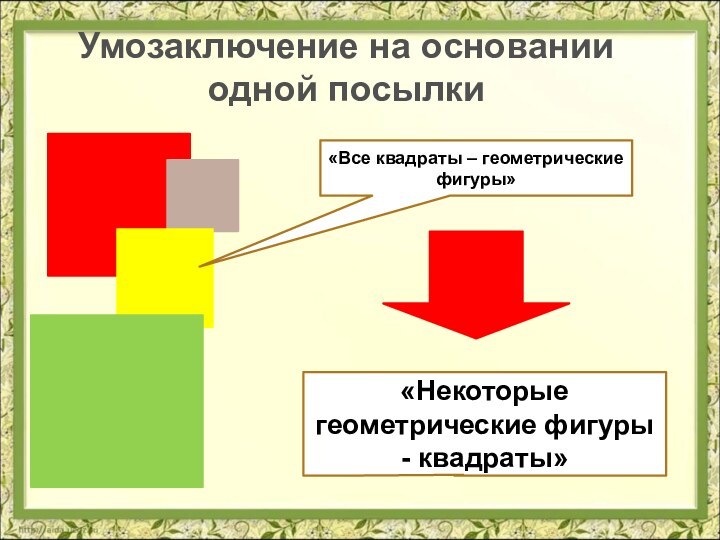
- 13. Умозаключение на основании одной посылки«Все квадраты – геометрические фигуры»«Некоторые геометрические фигуры - квадраты»
- 14. Объектами алгебры логики являются высказывания.Алгебру логики интересует
- 15. Простые высказывания в алгебре логики обозначаются заглавными
- 16. Составные высказывания на естественном языке образуются с
- 17. в естественном языке соответствует союзу И;в алгебре
- 19. в естественном языке соответствует союзу ИЛИ;в алгебре
- 20. В алгебре множеств дизъюнкции соответствует операция объединения
- 21. в естественном языке соответствует словам неверно, что…
- 23. в естественном языке соответствует обороту если …,
- 25. в естественном языке соответствует оборотам речи тогда
- 27. Логические операции имеют следующий приоритет:действия в скобках;инверсия (отрицание);&;V;;.
- 28. Урок 2Алгебра высказываний
- 29. 1. Найдите значения логических выражений:а) (1v 1)
- 30. 1. Даны истинные высказывания: А= «на улице
- 31. Сложные высказывания можно записывать в виде формул.
- 32. Для каждого составного высказывания (логического выражения) можно
- 33. Например, построим таблицу истинности для логической функции: Количество
- 36. Задание. Постройте таблицу истинности для данного логического выражения:
- 37. Тождественная истина При всех наборах значений
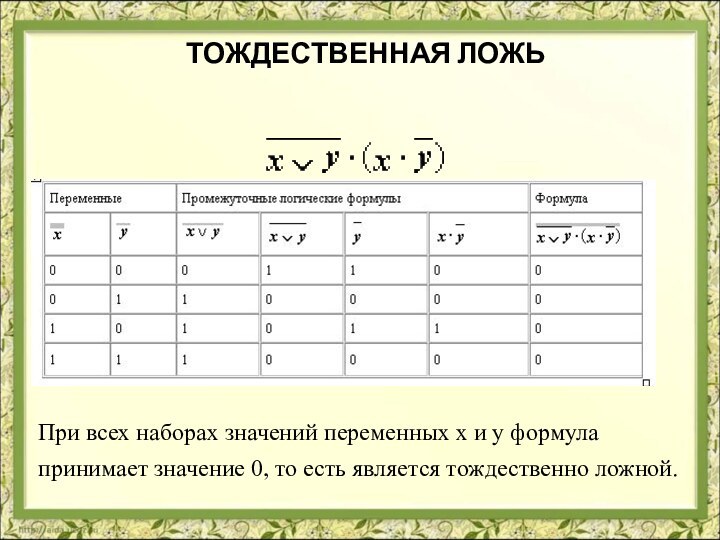
- 38. Тождественная ложь При всех наборах значений
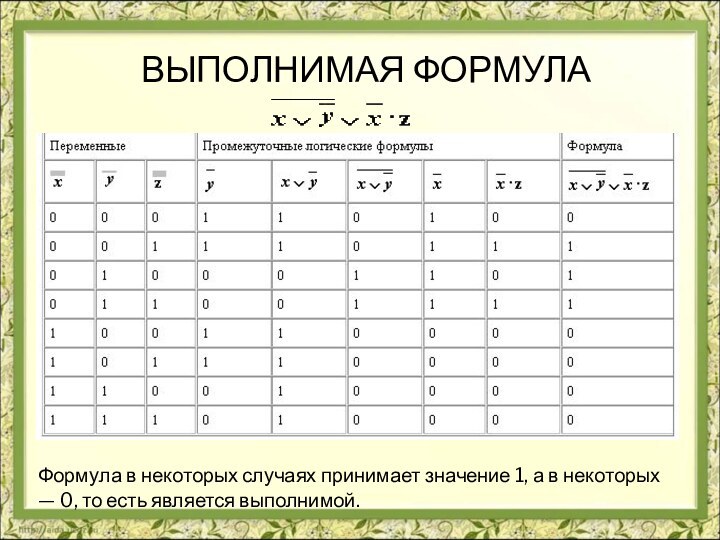
- 39. Выполнимая формулаФормула в некоторых случаях принимает значение
- 40. Скачать презентацию
- 41. Похожие презентации




































Слайд 3 Немецкий ученый и философ Готфрид - Вильгельм Лейбниц
(Gottfried Wilhelm von Leibniz) (1646-1716) начал развивать идею формализации
логики, размышляя о ее переводе "из словесного царства, полного неопределенностей, в царство математики, где отношения между объектами или высказываниями определяются совершенно точно". Лейбниц мечтал создать особый язык для выражения мыслей в чистом виде - lingua mentalis, с помощью которого можно было бы математически строго выразить любую мысль. При этом он уделял особое внимание двоичной системе счисления, считая ее основой основ для любого счета.
Слайд 4
Claude Elwood Shannon (1916 - 2001).
Является основателем
теории информации, нашедшей применение в современных высокотехнологических системах связи.
Шеннон внес огромный вклад в теорию вероятностных схем, теорию автоматов и теорию систем управления — области наук, входящие в понятие кибернетика.Слайд 5 Буль (Boole) Джордж (1815 — 1864) английский математик
и логик. Не имея специального математического образования, в 1849
стал профессором математики в Куинс-колледже в Корке (Ирландия), где преподавал до конца жизни. Д. Буля почти в равной мере интересовали логика, математический анализ, теория вероятностей, этика Б. Спинозы, философские работы Аристотеля и Цицерона.Слайд 6 Алгебра в широком смысле этого слова – наука
об общих операциях, аналогичных сложению и умножению, которые могут
выполняться над различными математическими объектами (алгебра переменных и функций, алгебра векторов, алгебра множеств и т.д.).Слайд 7 Логика – это наука о формах и способах
мышления
Формы мышления
понятие
суждение
(высказывание,
утверждение)
умозаключение
Слайд 8 Понятие - это форма мышления, которая выделяет существенные признаки
предмета или класса предметов, отличающие его от других.
Понятие
выражается одним или несколькими словами. Понятие имеет две стороны: содержание и объем.
Например: треугольник, компьютер, персональный компьютер, стол, дом и т.п.
Слайд 9 Суждения - это форма мышления, в которой утверждается или
отрицается связь между предметом и его признаком, отношения между
предметами или факт существования предмета и которая может быть либо истинной, либо ложной. Языковой формой выражения суждения является повествовательное предложение. Вопросительные и побудительные предложения суждениями не являются.Суждения рассматриваются не с точки зрения их смысла и содержания, а только с точки зрения их истинности или ложности. Истинным будет суждение, в котором связь понятий правильно отражает свойства и отношения реальных объектов. "Дважды два равно четырем" - истинное суждение, а вот "Процессор предназначен для печати" - ложное. Суждения могут быть простыми и сложными. "Весна наступила, и грачи прилетели" - сложное суждение, состоящее из двух простых.
Слайд 10
Какие из предложений являются высказываниями? Определите их истинность
1.
Число 6 – чётное.
Да 2. Посмотрите на доску.
Нет
3. Все роботы являются машинами.
Да
Слайд 11
Какие из предложений являются высказываниями? Определите их истинность
4.
У каждой лошади есть хвост.
Да5. Внимание!
Нет
6. Кто отсутствует?
Нет
Слайд 12
МОУ "Экономическая гимназия" Никифорова Л.Г,
Пример 1:заключение на основании
двух посылок:
Посылка: все
буквы - знаки.Посылка: «А» - это буква.
Заключение: буква «А» - это знак.
Пример 2:заключение на основании трех посылок:
Посылка: Буква – это часть слова.
Посылка: Слово – часть предложения.
Посылка: Предложение – часть текста.
Заключение: буква «А» - это текста.
Умозаключение
Слайд 13
Умозаключение на основании одной посылки
«Все квадраты – геометрические
фигуры»
«Некоторые геометрические фигуры - квадраты»
Слайд 14
Объектами алгебры логики являются высказывания.
Алгебру логики интересует только
один факт – истинно или ложно данное высказывание, что
дает возможность определять истинность или ложность составных высказываний алгебраическими методами.Слайд 15 Простые высказывания в алгебре логики обозначаются заглавными латинскими
буквами:
А= {Аристотель – основоположник
логики};В= {На яблонях растут бананы}.
Истинному высказыванию ставится в соответствие 1, ложному – 0.
Таким образом, А=1, В=0.
Слайд 16 Составные высказывания на естественном языке образуются с помощью
союзов, которые в алгебре высказываний заменяются на логические операции.
Логические
операции задаются таблицами истинности и могут быть проиллюстрированы с помощью диаграмм Эйлера-Венна.
Слайд 17
в естественном языке соответствует союзу И;
в алгебре высказываний
обозначение &;
в языках программирования обозначение And.
Конъюнкция – это логическая
операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.Логическая операция КОНЪЮНКЦИЯ (логическое умножение)
Слайд 18
Таблица истинности
А В
А&В0 0 0
0 1 0
1 0 0
1 1 1
В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.
Диаграмма Эйлера-Венна
Слайд 19
в естественном языке соответствует союзу ИЛИ;
в алгебре высказываний
обозначение V;
в языках программирования обозначение Or.
Дизъюнкция – это логическая
операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение)
Слайд 20 В алгебре множеств дизъюнкции соответствует операция объединения множеств,
т.е. множеству получившемуся в результате сложения множеств А и
В соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В.
Таблица истинности
А В АVВ
0 0 0
0 1 1
1 0 1
1 1 1
Диаграмма Эйлера-Венна
Слайд 21 в естественном языке соответствует словам неверно, что… и
частице не;
в алгебре высказываний обозначение Ā;
в языках программирования обозначение
Not.Отрицание – это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.
Логическая операция ИНВЕРСИЯ (отрицание)
Слайд 22
Таблица истинности
А Ā
0 1 1 0
В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.е. множеству получившемуся в результате отрицания множества А соответствует множество , дополняющее его до универсального множества.
Диаграмма Эйлера-Венна
Слайд 23 в естественном языке соответствует обороту если …, то
…;
обозначение .
Импликация – это логическая операция, ставящая в соответствие
каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (1-ое высказывание) истинно, а следствие (2-ое высказывание) ложно.Логическая операция ИМПЛИКАЦИЯ (логическое следование)
Слайд 25 в естественном языке соответствует оборотам речи тогда и
только тогда; в том и только в том случае;
обозначение
, ~.Эквиваленция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.
Логическая операция ЭКВИВАЛЕНЦИЯ (равнозначность)
Слайд 27
Логические операции имеют следующий приоритет:
действия в
скобках;
инверсия (отрицание);
&;
V;
;
.
Слайд 29
1. Найдите значения логических выражений:
а) (1v 1) v
(1 v O);
б) ((1 v O) v 1)
v 1; в) (0 v 1) v (1 v 0);
г) (0 & 1) & 1;
е) ((1 v O) & (1 & l)) & (O v 1);
ж) ((1&O) v (1&O)) v 1;
з) ((1&1) v O) & (O v 1);
и) ((0&0) v0) & (1 v 1).
2. Даны два простых высказывания:
А = {2 • 2 = 4}, В = {2 • 2 = 5}.
Какие из высказываний истинны:
а) А; б) В; в) А&В; г)AvB ; д) ¬A; е) A ^ В; ж) А ^ ¬В?
3. Даны простые высказывания:
А = {Принтер — устройство ввода информации},
В = {Процессор — устройство обработки информации},
С = {Монитор — устройство хранения информации},
D = {Клавиатура — устройство ввода информации}.
Определите истинность высказывания: (A & B) & (C v D).
Повторение по теме «Дизъюнкция, конъюнкция, отрицание»
Слайд 30 1. Даны истинные высказывания: А= «на улице идет
снег» и В = «нужно надеть шапку».
Составьте высказывания: а)
А=>B, б) B=>A, которые будут принимать ложные значения.2. Даны истинные высказывания А = «Карлсон хочет варенье» и В = «Карлсон летает на свежем воздухе». Составьте истинные высказывания вида A <=> B.
3. Даны простые высказывания:
А = {Принтер — устройство ввода информации},
В = {Процессор — устройство обработки информации},
С = {Монитор — устройство хранения информации},
D = {Клавиатура — устройство ввода информации}.
Определите истинность составных высказываний:
а) (AvB) <=> (C&D); б) А↔ В.
4. Даны простые высказывания:
А = {5>3}, В = {2=3} и С = {4<2}.
Определите истинность составных высказываний
a) (A v B) & C => (A & C) v (B & C); б) (A & B) v C ↔ (A v C) & (A &B ).
Повторение по теме
«Импликация и эквивалентность»
Слайд 31 Сложные высказывания можно записывать в виде формул. Для
этого простые логические высказывания нужно обозначить как логические переменные
буквами и связать их с помощью знаков логических операций. Такие формулы называются логическими выражениями. Например:Чтобы определить значение логического выражения необходимо подставить значения логических переменных в выражение и выполнить логические операции. Операции в логическом выражении выполняются слева направо с учетом скобок в следующем порядке: 1. инверсия; 2. конъюнкция; 3. дизъюнкция; 4. импликация и эквивалентность. Для изменения указанного порядка выполнения логических операций используются круглые скобки.
ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ И ТАБЛИЦЫ ИСТИННОСТИ
Слайд 32 Для каждого составного высказывания (логического выражения) можно построить
таблицу истинности, которая определяет истинность или ложность логического выражения
при всех возможных комбинациях исходных значений простых высказываний (логических переменных).При построении таблиц истинности целесообразно руководствоваться определенной последовательностью действий:
1) записать выражение и определить порядок выполнения операций
2) определить количество строк в таблице истинности. Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение (определяется по формулеQ=2n , где n - количество входных переменных)
3) определить количество столбцов в таблице истинности (= количество логических переменных + количество логических операций)
4) построить таблицу истинности, обозначить столбцы (имена переменных и обозначения логических операций в порядке их выполнения) и внести в таблицу возможные наборы значений исходных логических переменных.
5) заполнить таблицу истинности, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности
Теперь мы можем определить значение логической функции для любого набора значений логических переменных.
Таблицы истинности