- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Алгебра высказываний
Содержание
- 2. СОДЕРЖАНИЕВведение.Логическая операция конъюнкция.Логическая операция дизъюнкция.Логическая операция инверсия.Логическая операция импликация.Логическая операция эквиваленция.Конец.
- 3. АЛГЕБРА в широком смысле этого слова –
- 4. Алгебра логики отвлекается от смысловой содержательности высказываний.
- 5. Простые высказывания в алгебре логики обозначаются заглавными
- 6. Составные высказывания на естественном языке образуются с
- 7. Логическая операция КОНЪЮНКЦИЯ (логическое умножение)В естественном языке
- 8. Конъюнкция – это логическая операция, ставящая
- 9. Пример. Даны высказывания. Определите истинность каждого из
- 10. Таблица истинностисодержаниедальше
- 11. Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение)В естественном языке
- 12. Дизъюнкция – Дизъюнкция – это логическая
- 13. Пример. Даны высказывания. Определите истинность каждого из
- 14. Таблица истинностиТаблица истинностисодержаниедальше
- 15. Логическая операция ОТРИЦАНИЕ (инверсия)В естественном языке соответствует
- 16. Отрицание – это логическая операция, которая каждому простому истинному высказыванию ставит в соответствие ложное высказывание.
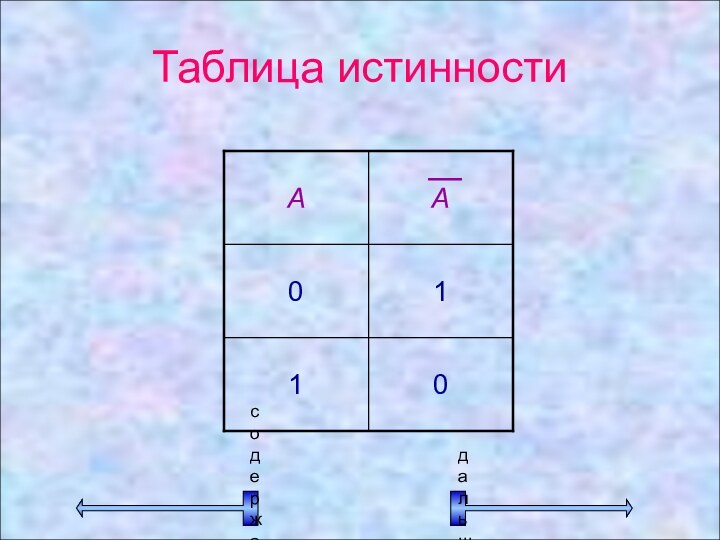
- 17. Пример А = {Луна – спутник Земли}А = {Луна – не спутник Земли}
- 18. Таблица истинностисодержаниедальше
- 19. Логическая операция ИМПЛИКАЦИЯ (логическое следование)Логическая операция ИМПЛИКАЦИЯ
- 20. Импликация – Импликация – это логическая
- 21. Пример. Даны высказывания. Пример. Даны высказывания. А
- 22. А истинно и В истинно, т. е.
- 23. В обычной речи связка «если …, то»
- 24. Таблица истинностиТаблица истинностидальшесодержание
- 25. Логическая операция ЭКВИВАЛЕНЦИЯ (равнозначность)Логическая операция ЭКВИВАЛЕНЦИЯ (равнозначность)В
- 26. Эквиваленция – Эквиваленция – это логическая
- 27. Пример. Определить истинность высказываний.Пример. Определить истинность высказываний.А
- 28. Таблица истинностиТаблица истинностисодержаниедальше
- 29. спасибо за внимание и активную работу!
- 30. Скачать презентацию
- 31. Похожие презентации

























Слайд 2
СОДЕРЖАНИЕ
Введение.
Логическая операция конъюнкция.
Логическая операция дизъюнкция.
Логическая операция инверсия.
Логическая операция
импликация.
Слайд 3
АЛГЕБРА в широком смысле этого слова – наука
об общих операциях, аналогичных сложению и умножению, которые могут
выполняться над различными математическими объектами (алгебра переменных и функций, алгебра векторов, алгебра множеств и так далее).Объектами алгебры логики являются высказывания.
Слайд 4
Алгебра логики отвлекается от смысловой содержательности высказываний. Ее
интересует только один факт – истинно или ложно данное
высказывание, что дает возможность определять истинность или ложность составных высказываний алгебраическими методами.
Слайд 5
Простые высказывания в алгебре логики обозначаются заглавными буквами
А = {Аристотель – основоположник логики}
В =
{На яблонях растут бананы}Истинному высказыванию ставится в соответствие 1, ложному – 0.
Таким образом, А = 1, В = 0.
Слайд 6
Составные высказывания на естественном языке образуются с помощью
союзов, которые в алгебре высказываний заменяются на логические операции.
Логические операции задаются таблицами истинности.
содержание
дальше
Слайд 7
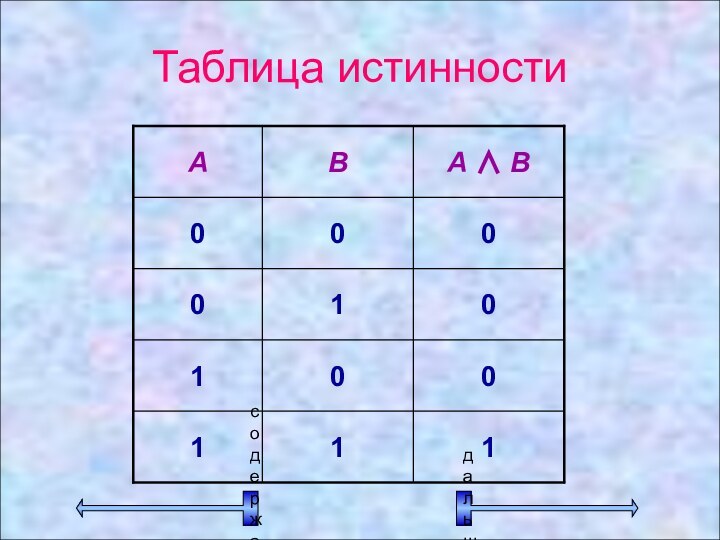
Логическая операция КОНЪЮНКЦИЯ (логическое умножение)
В естественном языке соответствует
союзу и
В алгебре высказываний обозначается
⋅ ∧ &В языках программирования обозначается and
Слайд 8
Конъюнкция –
это логическая операция, ставящая
в соответствие каждым двум простым высказываниям составное высказывание, являющееся
истинным тогда и только тогда, когда оба исходных высказывания истинны.
Слайд 9
Пример. Даны высказывания. Определите истинность каждого из них.
А
= {10 делится на 2 и 5 не больше
трех}В = {10 не делится на 2 и 5 больше трех}
С = {10 делится на 2 и 5 больше трех}
D = {10 не делится на 2 и 5 не больше трех}
А = 1 ∧ 0 = 0
В = 0 ∧ 1 = 0
С = 1 ∧ 1 = 1
D = 0 ∧ 0 = 0
Слайд 11
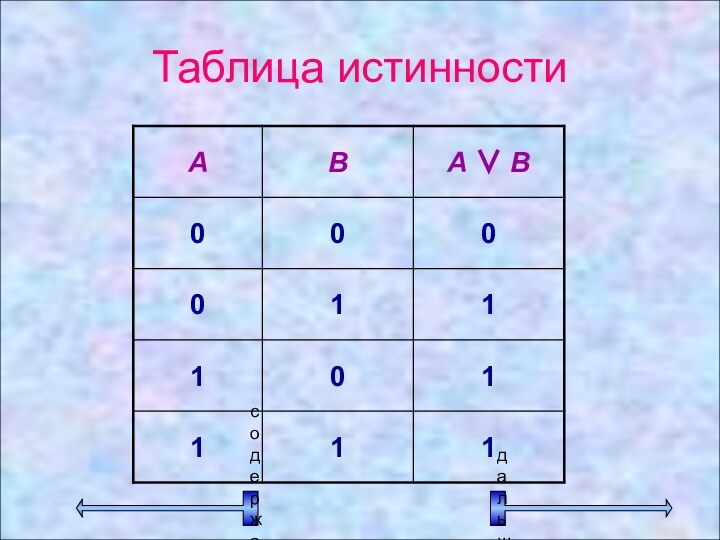
Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение)
В естественном языке соответствует
союзу или.
В алгебре высказываний обозначается
∨В языках программирования обозначается or.
Слайд 12
Дизъюнкция –
Дизъюнкция –
это логическая
операция, ставящая в соответствие каждым двум простым высказываниям составное
высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.
Слайд 13
Пример. Даны высказывания. Определите истинность каждого из них.
Пример.
Даны высказывания. Определите истинность каждого из них.
А = {10
делится на 2 или 5 не больше трех}В = {10 не делится на 2 или 5 больше трех}
С = {10 делится на 2 или 5 больше трех}
D = {10 не делится на 2 или 5 не больше трех}
A = 1 ∨ 0 = 1
B = 0 ∨ 1 = 1
C = 1 ∨ 1 = 1
D = 0 ∨ 0 = 0
Слайд 15
Логическая операция ОТРИЦАНИЕ
(инверсия)
В естественном языке соответствует частице не.
В
алгебре высказываний обозначается
А, ¬АВ языках программирования обозначается not
Слайд 16
Отрицание –
это логическая операция, которая
каждому простому истинному высказыванию ставит в соответствие ложное высказывание.
Слайд 19
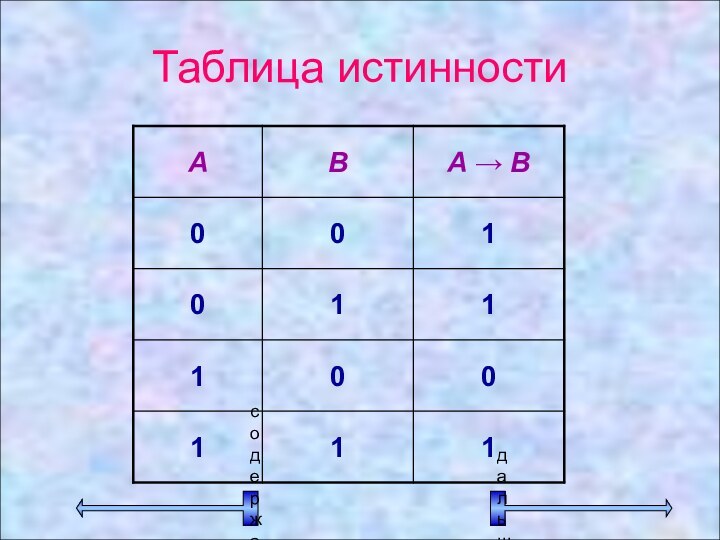
Логическая операция ИМПЛИКАЦИЯ
(логическое следование)
Логическая операция ИМПЛИКАЦИЯ
(логическое следование)
В естественном
языке соответствует обороту если …, то … .
В алгебре
высказываний обозначается⇒ →
В языках программирования не используется
Слайд 20
Импликация –
Импликация –
это логическая
операция, ставящая в соответствие каждым двум простым высказываниям составное
высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.
Слайд 21
Пример. Даны высказывания.
Пример. Даны высказывания.
А =
{Данный четырехугольник - квадрат}
В = {Около данного четырехугольника можно
описать окружность}Рассмотрим составное высказывание А → В , понимаемое как «если данный четырехугольник – квадрат, то около него можно описать окружность».
Есть три варианта, когда
высказывание А → В истинно
Слайд 22 А истинно и В истинно, т. е. если
данный четырехугольник – квадрат, то около него можно описать
окружность;А ложно и В истинно, т. е. если данный четырехугольник не является квадратом, то около него можно описать окружность;
А ложно и В ложно, т. е. если данный четырехугольник не является квадратом, то около него нельзя описать окружность;
А истинно и В истинно, т. е. если данный четырехугольник – квадрат, то около него можно описать окружность;
А ложно и В истинно, т. е. если данный четырехугольник не является квадратом, то около него можно описать окружность;
А ложно и В ложно, т. е. если данный четырехугольник не является квадратом, то около него нельзя описать окружность;
Ложен только один вариант: А истинно и В ложно, т. е. если данный четырехугольник – квадрат, то около него нельзя описать окружность.
Слайд 23
В обычной речи связка «если …, то» описывает
причинно-следственную связь между высказываниями. Но в логических операциях смысл
высказываний не учитывается. Рассматривается только их истинность или ложность. Поэтому не надо смеяться над бессмысленностью импликаций, образованных высказываниями, совершенно не связанными по содержанию.Например, такими:
«если президент США – демократ, то в Африке водятся жирафы»
или «если арбуз ягода, то в бензоколонке есть бензин»
Слайд 25
Логическая операция ЭКВИВАЛЕНЦИЯ
(равнозначность)
Логическая операция ЭКВИВАЛЕНЦИЯ
(равнозначность)
В естественном языке соответствует
оборотам речи тогда и только тогда; в том и
только в том случаеВ алгебре высказываний обозначается
⇔ ↔ ~
В языках программирования не используется
Слайд 26
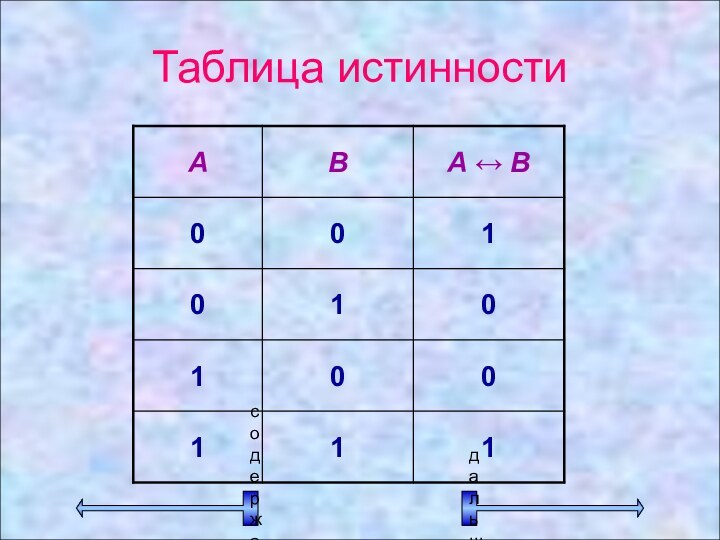
Эквиваленция –
Эквиваленция –
это логическая
операция, ставящая в соответствие каждым двум простым высказываниям составное
высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или ложны.
Слайд 27
Пример. Определить истинность высказываний.
Пример. Определить истинность высказываний.
А =
{24 делится на 6 тогда и только тогда, когда
24 делится на 3}А = 1 ↔ 1 = 1
В = {23 делится на 6 тогда и только тогда, когда 23 делится на 3}
В = 0 ↔ 0 = 1
С = {24 делится на 6 тогда и только тогда, когда 24 делится на 5}
С = 1 ↔ 0 = 0
D = {21 делится на 6 тогда и только тогда, когда 21 делится на 3}
D = 0 ↔ 1 = 0













![Вещественные числа. Стандарт IEEE 754. Команды и регистры математического сопроцессора [MASM]](/img/tmb/15/1448550/4185a9fa6859b70c0b4d268db72c5a49-210x.jpg)














