ориентированном ациклическом графе с n вершинами?
Может ли быть так,
что правильным результатом топологической сортировки графа оказывается любой порядок его вершин?Решить задачу о производстве деталей с помощью DFS.
Как использовать топологическую сортировку для определения наличия циклов в графе?



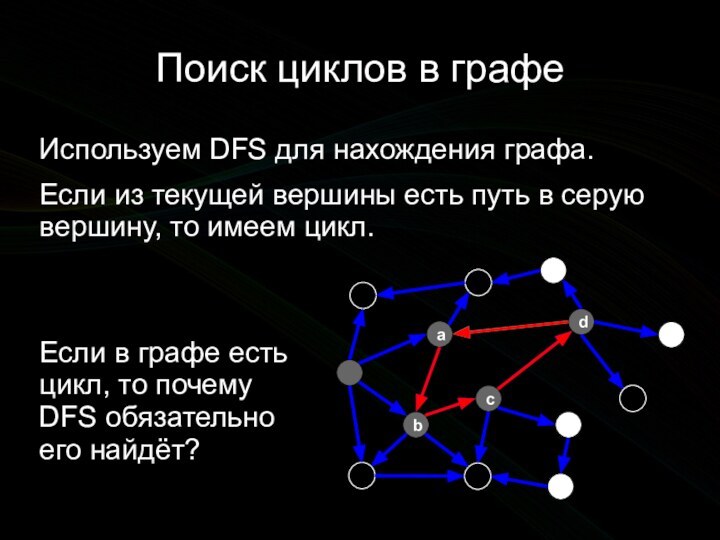
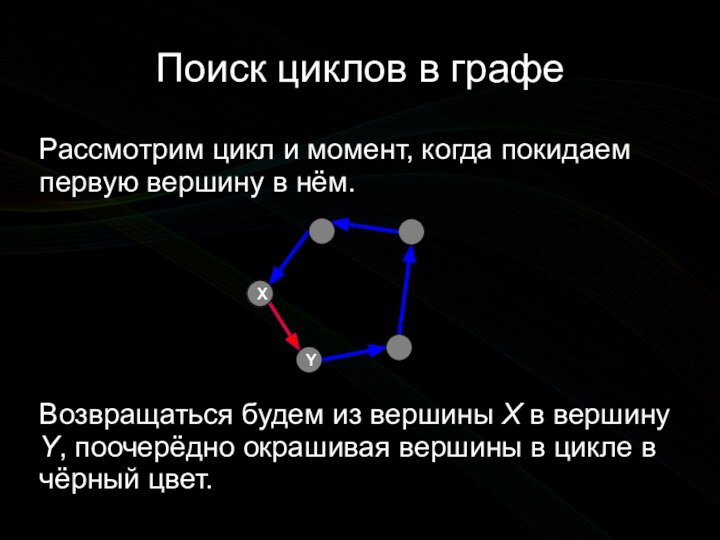

![Алгоритмы на графах. Определение наличия циклов в графе Поиск циклов в графеPascalfor i := 1 to n do color[i] :=](/img/tmb/11/1089472/57c90e89d639ce57ec5d45e3272af69e-720x.jpg)
































