- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Алгоритмы поиска пути. От поиска в ширину до A
Содержание
- 2. Графы: основыГраф – множество вершин и ребер. Ребра
- 3. Графы: примерыНеориентированный невзвешенныйОриентированный взвешенный
- 4. Графы в играхТайловая сетка(tile map, grid)
- 5. Графы в играхПолигональная карта(polygonal map)
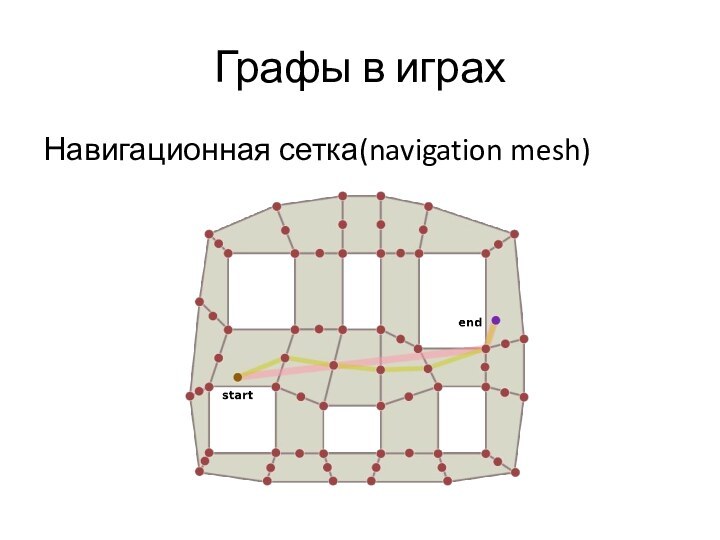
- 6. Графы в играхНавигационная сетка(navigation mesh)
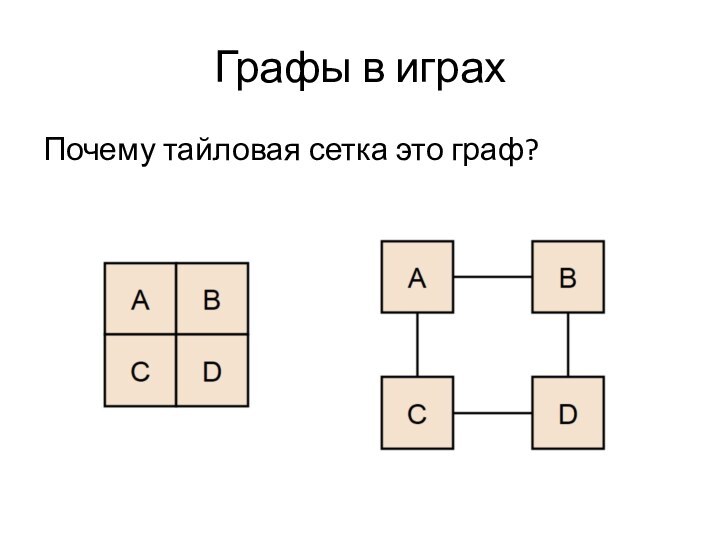
- 7. Графы в играхПочему тайловая сетка это граф?
- 8. Поиск кратчайшего пути: задача Есть вершина начала пути
- 9. Поиск кратчайшего пути: общие принципыРазбиваем клетки на
- 10. Поиск кратчайшего пути: обзорПоиск в ширину(breadth-first search)Алгоритм Дейкстры(Dijkstra's algorithm)Поиск первого наилучшего(best-first search)A*(A star)
- 11. Поиск в ширину: идеяРавномерно во все стороны
- 12. Поиск в ширину: демо
- 13. Поиск в ширину: демо
- 14. Поиск в ширину: демо
- 15. Поиск в ширину: демо
- 16. Поиск в ширину: кодПростейший вариант(инициализация) frontier = Queue() frontier.put(start) visited = {} visited[start] = True
- 17. Поиск в ширину: кодПростейший вариант(алгоритм) while not frontier.empty(): current
- 18. Поиск в ширину: кодЧтобы узнать, откуда пришли(инициализация) frontier = Queue() frontier.put(start) came_from = {} came_from[start] = None
- 19. Поиск в ширину: кодЧтобы узнать, откуда пришли
- 21. Поиск в ширину: кодЧтобы узнать кол-во шагов (инициализация) frontier = Queue() frontier.put(start) distance = {} distance[start] = 0
- 22. Поиск в ширину: кодЧтобы узнать кол-во шагов(алгоритм) while
- 24. Поиск в ширину: use casesОтметить все достижимые
- 25. Поиск в ширину: ограничения
- 26. Алгоритм Дейкстры: идеяИсследуем вершины не равномерно, а
- 27. Алгоритм Дейкстры: демо
- 28. Алгоритм Дейкстры: демо
- 29. Алгоритм Дейкстры: демо
- 30. Алгоритм Дейкстры: демо
- 31. Алгоритм Дейкстры: демо
- 32. Алгоритм Дейкстры: кодfrontier = PriorityQueue()frontier.put(start,0)came_from = {}cost_so_far = {}came_from[start] = Nonecost_so_far[start] = 0
- 33. Алгоритм Дейкстры: код while not frontier.empty(): current =
- 34. Алгоритм Дейкстры: use casesНайти кратчайший путь от
- 35. Алгоритм Дейкстры : ограниченияЕсли нужно найти путь до единственной вершины, исследуется слишком много клеток
- 36. Поиск первого наилучшего: идеяИсследуем вершины, ориентируясь на расстояние до целиИспользуем эвристику(heuristic)
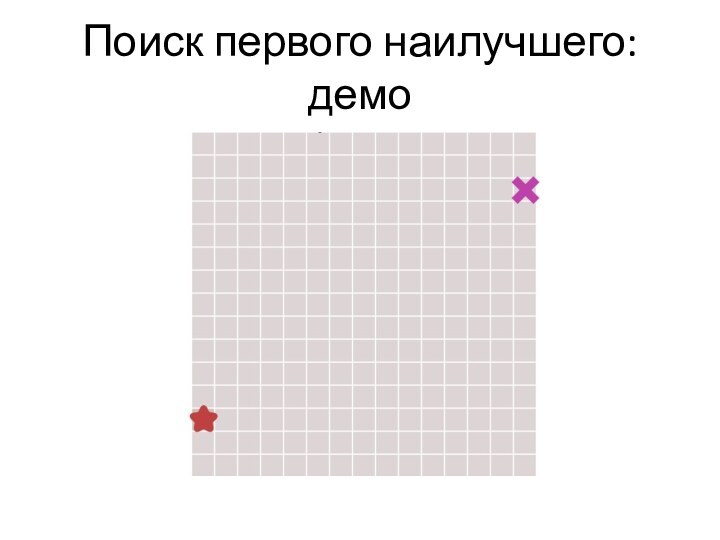
- 37. Поиск первого наилучшего: демо
- 38. Поиск первого наилучшего: демо
- 39. Поиск первого наилучшего: демо
- 40. Поиск первого наилучшего: демо
- 41. Поиск первого наилучшего: кодfrontier = PriorityQueue()frontier.put(start, 0)came_from = {}came_from[start] = None
- 42. Поиск первого наилучшего: код while not frontier.empty(): current
- 43. Поиск первого наилучшего: use casesБыстро найти кратчайший путь от одной вершины до другой, когда нет препятствий
- 44. Поиск первого наилучшего: ограничения Кратчайший путь не найден
- 45. A*: идеяИсследуем вершины не равномерно, а ориентируясь
- 46. A*: демо
- 47. A*: кодfrontier = PriorityQueue()frontier.put(start, 0)came_from = {}cost_so_far = {}came_from[start] = Nonecost_so_far[start] = 0
- 48. A*: код while not frontier.empty(): current = frontier.get() for
- 49. A*: use casesБыстро найти кратчайший путь от одной вершины до другой, даже если есть препятствия
- 50. A*: эвристикиЭвристики бывают разные. От выбора эвристики зависит корректность алгоритма и его быстрота.Манхэтонновское расстояние
- 51. A*: эвристикиДиагональное расстояние
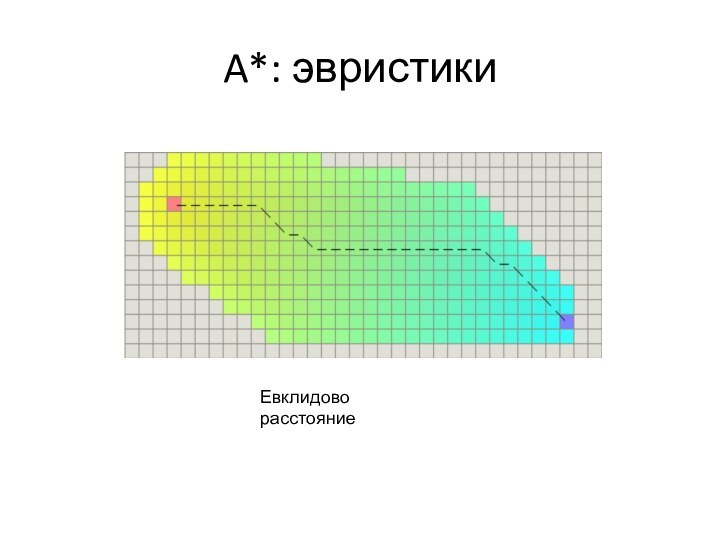
- 52. A*: эвристикиЕвклидово расстояние
- 53. Скачать презентацию
- 54. Похожие презентации
Графы: основыГраф – множество вершин и ребер. Ребра соединяют между собой вершины.Графы бывают разные:Неориентированные и ориентированныеВзвешенные и невзвешенные.
![Поиск в ширину: кодПростейший вариант(инициализация) frontier = Queue() frontier.put(start) visited = {} visited[start] = True](/img/tmb/15/1461775/fd84beb6f8109d8d13e1f8e6d539f631-720x.jpg "Алгоритмы поиска пути. От поиска в ширину до A")
![Поиск в ширину: кодЧтобы узнать, откуда пришли(инициализация) frontier = Queue() frontier.put(start) came_from = {} came_from[start] = None](/img/tmb/15/1461775/bca152b7e746c103376f664ec710c847-720x.jpg "Алгоритмы поиска пути. От поиска в ширину до A")
![Поиск в ширину: кодЧтобы узнать кол-во шагов (инициализация) frontier = Queue() frontier.put(start) distance = {} distance[start] = 0](/img/tmb/15/1461775/934f5138e8cb2ab0ba7eeb65e40fff09-720x.jpg "Алгоритмы поиска пути. От поиска в ширину до A")
![Алгоритм Дейкстры: кодfrontier = PriorityQueue()frontier.put(start,0)came_from = {}cost_so_far = {}came_from[start] = Nonecost_so_far[start] = 0](/img/tmb/15/1461775/3a8a6df602f4e2617a5a62886897d4ae-720x.jpg "Алгоритмы поиска пути. От поиска в ширину до A")
![Поиск первого наилучшего: кодfrontier = PriorityQueue()frontier.put(start, 0)came_from = {}came_from[start] = None](/img/tmb/15/1461775/eefab7b149882938ab0444f5f36f2abb-720x.jpg "Алгоритмы поиска пути. От поиска в ширину до A")
![A*: кодfrontier = PriorityQueue()frontier.put(start, 0)came_from = {}cost_so_far = {}came_from[start] = Nonecost_so_far[start] = 0](/img/tmb/15/1461775/d2053a8638c8d9557e731146a656a102-720x.jpg "Алгоритмы поиска пути. От поиска в ширину до A")
![A*: код while not frontier.empty(): current = frontier.get() for next in graph.neighbors(current): new_cost = cost_so_far[current]](/img/tmb/15/1461775/2e07d14c22521840afe8cde40e7fd8e6-720x.jpg "Алгоритмы поиска пути. От поиска в ширину до A")
Слайд 8
Поиск кратчайшего пути: задача
Есть вершина начала пути и
вершина конца пути. Нужно найти кратчайший путь от начала
до конца.
Слайд 9
Поиск кратчайшего пути: общие принципы
Разбиваем клетки на два
типа: посещенные и непосещенные.
Постепенно посещаем клетки.
Изначально только стартовая клетка
посещена.
Слайд 10
Поиск кратчайшего пути: обзор
Поиск в ширину(breadth-first search)
Алгоритм Дейкстры(Dijkstra's algorithm)
Поиск
первого наилучшего(best-first search)
A*(A star)
Слайд 11
Поиск в ширину: идея
Равномерно во все стороны расширяется
радиус обхода.
Посещенные вершины хранятся в очереди(queue).
Заканчиваем, когда очередь пуста(изначально
в очереди находится стартовая клетка).
Слайд 16
Поиск в ширину: код
Простейший вариант(инициализация)
frontier = Queue()
frontier.put(start)
visited =
{}
visited[start] = True
Слайд 17
Поиск в ширину: код
Простейший вариант(алгоритм)
while not frontier.empty():
current =
frontier.get()
for next in graph.neighbors(current):
if next not in visited:
frontier.put(next)
visited[next] =
True
Слайд 18
Поиск в ширину: код
Чтобы узнать, откуда пришли(инициализация)
frontier =
Queue()
frontier.put(start)
came_from = {}
came_from[start] = None
Слайд 19
Поиск в ширину: код
Чтобы узнать, откуда пришли (алгоритм)
while
not frontier.empty():
current = frontier.get()
for next in graph.neighbors(current):
if next not
in came_from:frontier.put(next)
came_from[next] = current
Слайд 21
Поиск в ширину: код
Чтобы узнать кол-во шагов (инициализация)
frontier
= Queue()
frontier.put(start)
distance = {}
distance[start] = 0
Слайд 22
Поиск в ширину: код
Чтобы узнать кол-во шагов(алгоритм)
while not
frontier.empty():
current = frontier.get()
for next in graph.neighbors(current):
if next not in
distance:frontier.put(next)
distance[next] = distance[current] + 1
Слайд 24
Поиск в ширину: use cases
Отметить все достижимые вершины
из данной вершины
Найти пути и расстояния до всех вершин
из данной вершины(просмотреть, что находится рядом с героем/монстром)
Слайд 26
Алгоритм Дейкстры: идея
Исследуем вершины не равномерно, а ориентируясь
на расстояние до начала поиска
Посещенные вершины хранятся в очереди
с приоритетом(min priority queue) – чем меньше расстояние до вершины, тем больше ее приоритет. Т. е. тем раньше эта вершина будет исследована.
Слайд 32
Алгоритм Дейкстры: код
frontier = PriorityQueue()
frontier.put(start,0)
came_from = {}
cost_so_far =
{}
came_from[start] = None
cost_so_far[start] = 0
Слайд 33
Алгоритм Дейкстры: код
while not frontier.empty():
current = frontier.get()
for
next in graph.neighbors(current):
new_cost = cost_so_far[current] + graph.cost(current, next)
if next
not in cost_so_far or new_cost < cost_so_far[next]: cost_so_far[next] = new_cost
frontier.put(next, new_cost)
came_from[next] = current
Слайд 34
Алгоритм Дейкстры: use cases
Найти кратчайший путь от одной
вершины до многих других вершин во взвешенном графе
Когда нет
знания об общей структуре графа. Т. е. мы обладаем лишь локальной информацией о графе(вблизи каждой клетки)
Слайд 35
Алгоритм Дейкстры : ограничения
Если нужно найти путь до
единственной вершины, исследуется слишком много клеток
Слайд 36
Поиск первого наилучшего: идея
Исследуем вершины, ориентируясь на расстояние
до цели
Используем эвристику(heuristic)
Слайд 41
Поиск первого наилучшего: код
frontier = PriorityQueue()
frontier.put(start, 0)
came_from =
{}
came_from[start] = None
Слайд 42
Поиск первого наилучшего: код
while not frontier.empty():
current =
frontier.get()
for next in graph.neighbors(current):
new_cost = cost_so_far[current] + graph.cost(current, next)
if
next not in came_from:priority = heuristic(goal, next)
frontier.put(next, priority)
came_from[next] = current
Слайд 43
Поиск первого наилучшего: use cases
Быстро найти кратчайший путь
от одной вершины до другой, когда нет препятствий
Слайд 45
A*: идея
Исследуем вершины не равномерно, а ориентируясь на
расстояние до начала поиска…
И на расстояние до цели. Т.е.
используем эвристику.Сочетание алгоритма Дейкстры и поиска первого наилучшего.
Слайд 47
A*: код
frontier = PriorityQueue()
frontier.put(start, 0)
came_from = {}
cost_so_far =
{}
came_from[start] = None
cost_so_far[start] = 0
Слайд 48
A*: код
while not frontier.empty():
current = frontier.get()
for next
in graph.neighbors(current):
new_cost = cost_so_far[current] + graph.cost(current, next)
if next not
in cost_so_far or new_cost < cost_so_far[next]:cost_so_far[next] = new_cost
priority = new_cost + heuristic(goal, next)
frontier.put(next, priority)
came_from[next] = current
Слайд 49
A*: use cases
Быстро найти кратчайший путь от одной
вершины до другой, даже если есть препятствия
Слайд 50
A*: эвристики
Эвристики бывают разные. От выбора эвристики зависит
