Слайд 2
Раздел 20. Анализ корреляции экспериментальных и расчетных результатов
ВВЕДЕНИЕ
В АНАЛИЗ КОРРЕЛЯЦИИ ЭКСПЕРИМЕНТАЛЬНЫХ И
РАСЧЕТНЫХ РЕЗУЛЬТАТОВ..………………………….………………………………...…… 20 - 3
ИНТЕГРАЦИЯ
РАСЧЕТОВ И ИСПЫТАНИЙ...…………………………………………..…… 20 - 5
ПЛАНИРОВАНИЕ ИСПЫТАНИЙ…………………………………………………………….… 20 - 6
АНАЛИЗ РЕЗУЛЬТАТОВ ИСПЫТАНИЙ..…………………………………………………… 20 - 9
ВЫВОДЫ.………………………………………………………………………………………… 20 - 18
УТОЧНЕНИЕ РАСЧЕТНОЙ МОДЕЛИ……………………………………………………….. 20 - 19
ЛИТЕРАТУРА.…………………………………………………………………………………… 20 - 27
Слайд 3
Введение в анализ корреляции экспериментальных и расчетных результатов
Результаты,
полученные с помощью MSC.Nastran, и опытные данные могут не
совпадать вследствие недостатков моделирования и проведения испытаний.
Известно выражение: “Никто, за исключением инженера-аналитика, не верит результатам расчетов; все, кроме испытателя, верят экспериментальным данным”
Источники возникновения трудностей моделирования:
Физическая природа явления
Граничные условия
Свойства материалов
Податливость соединений
Задумано конструктором сделано производственником
Демпфирование
Слайд 4
Введение в анализ корреляции экспериментальных и расчетных результатов
Цели
анализа корреляции экспериментальных и расчетных результатов:
Исследовать степень корреляции между
результатами, полученными с помощью MSC.Nastran, и опытными данными.
Уточнить модель для лучшей согласованности данных расчетов и испытаний.
Инженер, исследующий корреляцию, должен понимать данные эксперимента, расчета и знать возможные источники ненадежности как в тех, так и в других.
Слайд 5
Интеграция расчетов и испытаний
Четыре этапа интеграции расчетов и
испытаний:
Планирование эксперимента (моделирование испытаний)
Сбор (регистрация) данных, например,
с помощью датчиков ускорений.
Обработка и анализ опытных данных (например, определение форм колебаний по экспериментальным данным)
Анализ результатов испытаний (оценка уровня согласованности результатов расчетов с помощью MSC.Nastran и опытных данных, уточнение модели для улучшения сходимости данных)
Инженер-аналитик участвует в 1-м и 4-м этапах, этапы 2 и 3 – за инженером-испытателем.
Слайд 6
Планирование испытаний
Создание исходной модели для определения оптимального воздействия
на объект и расположения датчиков. Для этого есть два
метода:
Моделирование и экспертный анализ
Проверка кросс-ортогональности
Моделирование и экспертный анализ: используя MSC.Nastran, моделируйте испытания и ищите способ воздействия и расположение датчиков для получения максимального отклика.
Проверка кросс-ортогональности:
На базе планируемого расположения датчиков создайте A-set. Затем, используя редуцирование Гайана, вычислите собственные формы во всем интересующем частотном диапазоне, нормализуйте их по массе. Назовите эти результаты (Ft) “тест”-модами.
Затем, удалив A-set, повторите вычисление собственных форм, выводя результаты только для тех степеней свободы, которые входили в A-set при предыдущем расчете. Назовите эти результаты (Fa) “расчетными” модами.
Слайд 7
Планирование испытаний
При третьем запуске MSC.Nastran “прочитайте” данные и
вычислите:
Если планируемое расположение датчиков (A-set) адекватное, диагональные члены полученной
матрицы будут равны 1, а внедиагональные – 0. Если внедиагональные члены матрицы не равны 0, то предлагаемое расположение датчиков неадекватное и должно быть пересмотрено. (На практике приемлемо, если внедиагональные члены меньше 0,05).
В комплекте с MSC.Nastran поставляется процедура на языке DMAP (premaca.vxx) для выполнения планирования испытаний.
Слайд 8
Планирование испытаний
Для лучшего понимания поведения объекта испытаний в
MSC.Nastran могут быть также вычислены эффективная модальная масса1 и
модальная кинетическая энергия2.
Для облегчения планирования испытаний и анализа их результатов расположение датчиков и их ориентация должны полностью соответствовать соответствующим допущениям при проведении расчетного анализа. Для выполнения этих требований в расчетной модели могут использоваться элементы RBAR, межузловые связи (MPC), альтернативные системы координат.
После того, как определятся места расположения датчиков и приложения воздействий, испытания д.б. промоделированы для того, чтобы убедиться, что образец в процессе их проведения не будет перегружен (и, следовательно, поврежден).
1.Для i-ой моды эффективная масса равна
где M – матрица масс и Dm – вектор колебаний жесткого тела.
2.Для i-ой моды кинетическая энергия равна
Слайд 9
Анализ результатов испытаний
Сравнение результатов расчетов, полученных с помощью
MSC.Nastran, и результатов испытаний путем экспертной оценки или проверки
кросс-ортогональности.
Экспертная оценка с использованием графических возможностей
Графики:
Нарисуйте опытные и расчетные данные на одном графике и сравните степень их соответствия по величине и частотному составу.
Убедитесь, что сравниваемые зависимости соответствуют по расположению и ориентации.
Графические изображения конструкции:
Нарисуйте расчетные о экспериментально полученные формы колебаний и сравните их на предмет соответствия (можно также использовать возможности анимации).
Экспертным оценкам могут быть подвергнуты и “неграфические” результаты, такие, например, как значения резонансных частот.
Слайд 10
Анализ результатов испытаний
Проверка кросс-ортогональности
Величина, подлежащая проверке на кросс-ортогональность
при анализе корреляции опытных и расчетных данных, определяется как
где Ft - экспериментально
полученные моды
Maa - матрица масс, соответствующая A-set
Fa - моды, полученные расчетом для A-set
Для соответствия расчетных и опытных данных внедиагональные члены должны быть меньше 10% от диагональных членов.
Порядок чередования “расчётных” и “опытных” мод может быть нарушен, что приведет к большим значениям внедиагональных членов матрицы корреляции COR.
При несоответствии опытных и расчетных данных может возникнуть необходимость уточнения расчетной модели.
Слайд 11
Анализ результатов испытаний
Пример анализа матрицы COR
Рассмотрим плоскую модель
балки. Положим, что датчики ускорений в направлениях X и
Y располагаются в каждом четном узле.
Слайд 12
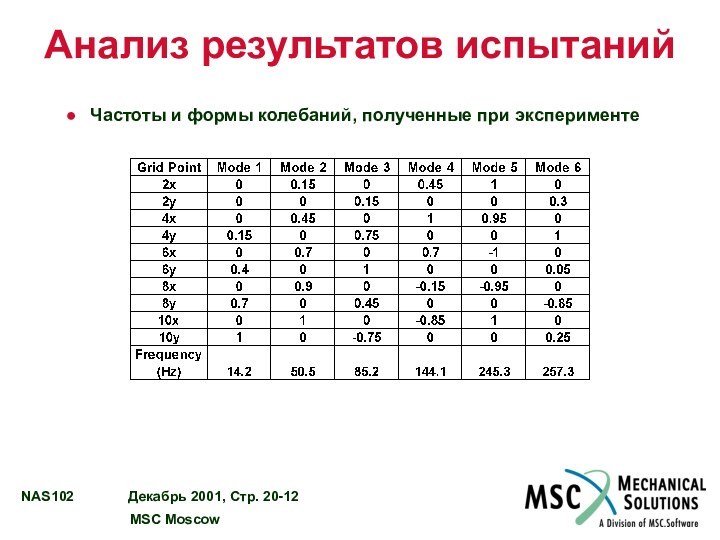
Анализ результатов испытаний
Частоты и формы колебаний, полученные при
эксперименте
Слайд 13
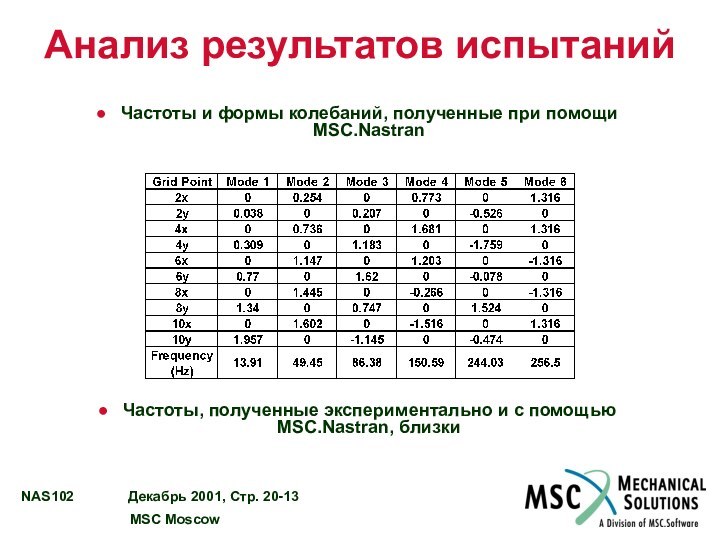
Анализ результатов испытаний
Частоты и формы колебаний, полученные при
помощи MSC.Nastran
Частоты, полученные экспериментально и с помощью MSC.Nastran, близки
Слайд 14
ID PRETEST, DYNOTES
SOL 103
TIME 15
COMPILE MODERS,
SOUIN=MSCSOU, NOLIST, NOREF
ALTER ’mxx.*phix’$
MATPRN MXX,,,,//$
MATPCH MXX,PHIX,,,// $
CEND
TITLE = MSC.Nastran
----- MSC/XL
SUBTITLE = MODES CASE CONTROL
LABEL = DEFAULT SUBCASE STRUCTURE
DISP = ALL
SPC=1
METHOD=100
BEGIN BULK
PARAM AUTOSPC YES
GRDSET, , , , , , ,345
BAROR, , , , , 0., 1., 0.
GRID 1 0.0 0.0 0.0
GRID 2 1. 0.0 0.0
GRID 3 2. 0.0 0.0
GRID 4 3. 0.0 0.0
GRID 5 4. 0.0 0.0
GRID 6 5. 0.0 0.0
GRID 7 6. 0.0 0.0
GRID 8 7. 0.0 0.0
GRID 9 8. 0.0 0.0
GRID 10 9. 0.0 0.0
GRID 11 10. 0.0 0.0
CBAR 1 1 1 2
CBAR 2 1 2 3
CBAR 3 1 3 4
CBAR 4 1 4 5
CBAR 5 1 5 6
CBAR 6 1 6 7
CBAR 7 1 7 8
CBAR 8 1 8 9
CBAR 9 1 9 10
CBAR 10 1 10 11
$ REDUCE TO TEST DOF
ASET1, 12, 2, 4, 6, 8, 10
SPC 1 1 123456 0.0
PBAR 1 1 .01 .016 .016
MAT1 1 3.+7 .3 7.7
EIGRL 100 0.0 10000. 6
ENDDATA
Анализ результатов испытаний
Замечание: Расположение узлов, входящих в A-set, такое же,
как и датчиков при испытаниях.
Слайд 15
Анализ результатов испытаний
ID COR, DYN.NOTES
TIME 30
SOL 100
COMPILE USERDMAP,

SOUIN=MSCSOU, NOLIST, NOREF
ALTER 2 $
$----------------------------------------------------------
$ DMAP TO COMPUTE CROSS-ORTHOGONALITY
$
INPUTS FROM MSC.Nastran RUN: MXX (A-SET MASS)
$ PHIX (A-SET MODE SHAPES)
$ (PREVIOUS M/N RUN USED MATPCH TO PUNCH DMI ENTRIES)
$ INPUT FROM TEST: PHITEST (A-SET MODE SHAPES)
$ OUTPUTS: UNITCHK (UNIT MASS CHECK)
$ COR (CROSS-ORTHOGONALITY MATRIX)
$----------------------------------------------------------
$ READ DMI INPUT
DMIIN DMI,DMINDX/PHIX,PHITEST,MXX,,,,,,,/ $
$ VERIFY INPUT MATRICES
MATPRN PHIX,PHITEST,MXX,,// $
$ MULTIPLY PHIX(TRANS)*MXX = PHITMASS
MPYAD PHIX,MXX,/ PHITMASS /1///$
$ MULTIPLY PHITMASS*PHIX = UNITCHK
MPYAD PHITMASS,PHIX,/ UNITCHK // $
$ PRINT TITLE AND UNITCHK
MATPRN UNITCHK,,,,// $
MESSAGE // ’CHECK ON UNIT MASS’/ $
$ MULTIPLY PHITMASS*PHITEST = COR
MPYAD PHITMASS,PHITEST,/ COR // $
$ PRINT TITLE AND COR
MATPRN COR,,,,// $
MESSAGE // ’CROSS-ORTHOGONALITY MATRIX’/ $
ENDALTER
CEND
TITLE = CROSS-ORTHOGONALITY CHECK
BEGIN BULK
DMI,PHITEST,0,2,1,0,,10,6
DMI,PHITEST,1,1,0.,.0,0.,.15,0.,
,.40,0.,.70,0.,1.0
DMI,PHITEST,2,1,.15,0.,.45,0.,.70,
,0.,.90,0.,1.0,0.
.
. (rest of PHITEST)
.
0 6
1 0 10 10
DMI* MXX 1 1 9.62499976E-02
* 3 1.92499999E-02
DMI* MXX 2 2 1.38867334E-01
* 4 2.67470982E-02 6 -1.37760025E-02
* 8 4.32037748E-03 10 3.94638191E-05
.
. (rest of MXX)
.
DMI PHIX 0 2 1 0 10 6
DMI* PHIX 1 1 -1.02694275E-17
* 3.79799381E-02 -3.21330419E-17 3.09179097E-01 1.62494801E-17
* 7.69559503E-01 -1.60461922E-17 1.34014440E+00 -4.83748987E-17
* 1.95740056E+00
DMI* PHIX 2 1 2.53673702E-01
* -3.71932167E-18 7.36189783E-01 -2.11487186E-17 1.14664245E+00
* -1.32509834E-17 1.44485378E+00 -5.04831637E-19 1.60163271E+00
* 1.19194476E-17
.
. (rest of PHIX)
.
ENDDATA
Анализ результатов испытаний
Слайд 17
Анализ результатов испытаний

MATRIX COR (GINO NAME 101 ) IS A DB PREC 6 COLUMN X 6 ROW SQUARE MATRIX.
COLUMN 1 ROWS 1 THRU 6 --------------------------------------------------
ROW
1) 5.1380D-01 6.7188D-19 1.8822D-03 -1.6038D-17 8.3091D-03 -1.5467D-16
COLUMN 2 ROWS 1 THRU 6 --------------------------------------------------
ROW
1) -1.0247D-17 6.1972D-01 3.1542D-18 -5.7035D-03 -1.0390D-17 -8.8287D-09
COLUMN 3 ROWS 1 THRU 6 --------------------------------------------------
ROW
1) -1.5467D-02 -6.3725D-18 6.3014D-01 -2.7673D-17 -4.6145D-03 9.5503D-17
COLUMN 4 ROWS 1 THRU 6 --------------------------------------------------
ROW
1) 2.5192D-18 1.1390D-02 8.1214D-17 5.8007D-01 -1.0636D-16 7.5993D-03
COLUMN 5 ROWS 1 THRU 6 --------------------------------------------------
ROW
1) -1.0452D-17 5.3899D-03 -2.1283D-17 -1.3447D-02 1.2668D-14 7.4474D-01
COLUMN 6 ROWS 1 THRU 6 --------------------------------------------------
ROW
1) -3.2927D-03 -2.5409D-18 8.7221D-03 -2.3220D-16 -5.6143D-01 9.6348D-15
THE NUMBER OF NON-ZERO TERMS IN THE DENSEST COLUMN = 6
THE DENSITY OF THIS MATRIX IS 100.00 PERCENT.
^^^CROSS-ORTHOGONALITY MATRIX
Слайд 18
Выводы
1. Матрица COR указывает на хорошее совпадение форм
(внедиагональные члены малы по сравнению с диагональными).
2.
“Опытная” мода 5 - это “расчетная” мода 6 наоборот. На это
указывают большие значения членов (5,6) и (6,5) матрицы COR.
3. Величина диагональных членов не равна 1,0 потому что “опытные”
моды не нормализованы до единичной массы (они нормализованы
до единичного максимального компонента).
4. Для подготовки к вводу опытных данных с помощью оператора
DMI необходима их некоторая предварительная обработка.
5. Для анализа большого количества мод может быть разработана
дополнительная процедура на языке DMAP для упрощения вида
результатов расчета кросс-корреляции.
6. Процедура на языке DMAP для выполнения проверки кросс-
корреляции (postmaca.vxx) – одна из поставляемых частей
MSC.Nastran.
Слайд 19
Уточнение расчетной модели
Существует три пути улучшения расчетной модели
для достижения соответствия расчетных и опытных данных:
1. Использование “грубой” силы
2. Использование
матрицы чувствительности
3. Использование методики оптимизации
Все методы подразумевают изменение параметров модели таких как I и A для BAR’ов и t для QUAD’ов. Упругость основания также может рассматриваться в качестве параметра, если она в явном виде представлена в модели (например, с помощью ELAS’ов).
Метод “грубой” силы:
Изменения модели производятся на базе экспертных оценок и результатов “прикидочных” расчетов.
После изменения модели расчет с помощью MSC.Nastran повторяется и его результаты анализируются на предмет лучшего согласования с опытными данными.
Если согласие данных не улучшается, - новые изменения и т.д.
Слайд 20
Уточнение расчетной модели
Матрица чувствительности:
Чувствительность – это градиент отклика
по параметру модели. “Отклики” – это результаты вычислений с
помощью MSC.Nastran, а “параметры” – значения свойств.
Каждое значение в матрице чувствительности S определяется как
где Ri - i-ый отклик и Pj - j-ый параметр.
Чем больше величина Sij, тем больше чувствительность отклика.
SOL 200 в MSC.Nastran вычисляет матрицу чувствительности.
Матрица S может использоваться для оценки того, какой параметр необходимо изменить для изменения соответствующего отклика.
Слайд 21
Уточнение расчетной модели
Матрица S также может быть получена
и использована посредством метода наименьших квадратов для минимизации разницы
между результатами испытаний и расчетов:
Pn = Po + (STS)-1ST(Rt - Ra)
где Pn - новое значение параметра, подлежащего
изменению
Po - значение параметра до изменения
S - матрица чувствительности
Rt - “опытный” отклик
Ra - “расчетный” отклик
Слайд 22
Уточнение расчетной модели
Использование оптимизации:
“Инструмент” - SOL 200
Цель: минимизация
разницы между опытными и расчетными результатами, но при минимальных
изменениях в исходной модели
Оператор DEQATN используется для записи целевой функции в виде “взвешенной” разности между опытными и расчетными результатами.
где RTi - i-ый результат испытаний
PFj - j-ый параметр модели после уточнения
RAi - i-ый расчетный результат
POj - исходное значение j-го параметра
WRi - весовой коэффициент для i-го испытания
WPj - весовой коэффициент для j-го параметра
wt - весовой коэффициент для всех опытных данных
wp - весовой коэффициент для всех параметров
SOL 200 минимизирует целевую функцию (E) с учётом ограничений.
Слайд 23
Уточнение расчетной модели
Пример
Модель корпуса дисковода, включающая 1406 узлов,
1354 оболочечных элементов,четыре переменных проектирования (толщины оболочек) и четыре
упругих моды, полученные в результате эксперимента
Необходимо минимизировать разницу между частотами собственных колебаний, вычисленными с помощью MSC.Nastran и полученными экспериментально.
Слайд 24
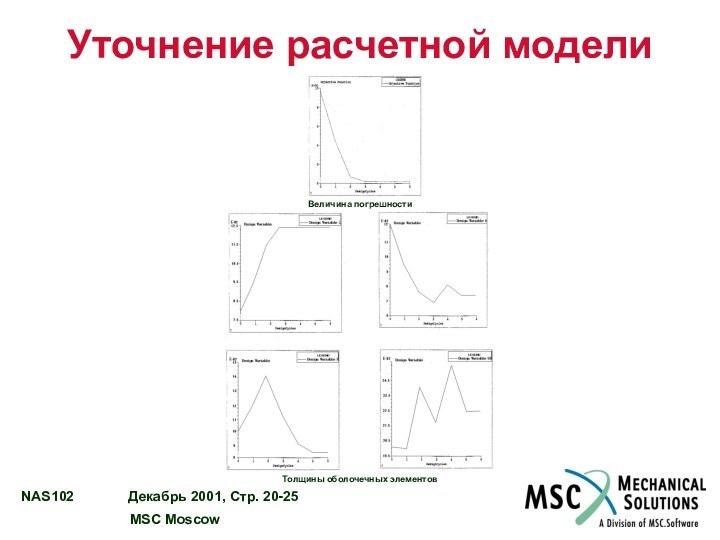
Уточнение расчетной модели
Пример
Весовой коэффициент для опытных данных в
100 раз больше весового коэффициента для параметров.
Учитываются верхние и
нижние ограничения на допустимую толщину оболочечных элементов.
После 5 итераций (шагов) достигнута сходимость
Результаты:
Слайд 26
Уточнение расчетной модели
SOL 200 может также использоваться для
улучшения корреляции с экспериментальными результатами по определению частотного отклика.
Возможно
использование для улучшения корреляции статических результатов.
Для достижения лучших результатов необходимо использовать как можно больше опытных данных (включая вес конструкции).
В качестве оптимизируемых необходимо рассматривать только те параметры, в значениях которых действительно есть неуверенность.
Слайд 27
Литература
Blakely, K. and Dobbs, M., “Integrated System Identification:
The Union of Testing and Analysis,” Proceedings First International
Modal Analysis Conference, November 1982.
Kientzy, D., Richardson, M. and Blakely, K., “Using Finite Element Data to Set Up Modal Tests,” Sound and Vibration, June 1989.
Blakely, K., “Updating MSC.Nastran Models to Match Test Data,” Proceedings MSC World Users’ Conference, March 1991.
Blakely, K. and Rose, T., “Cross-Orthogonality Calculations for Pre-Test Planning and Model Verification,” Proceedings MSC World Users’ Conference, May 1993.
Blakely, K., “Matching Frequency Response Test Data with MSC.Nastran,” Proceedings MSC World Users’ Conference, June 1994.