Слайд 2
Основные понятия.
Определение 1. Системой счисления называется совокупность цифровых
знаков и правил их запи-си, применяемая для однозначного изображения
чисел.
Определение 2. Под системой счисления пони-мается способ представления любого числа посре-дством некоторого алфавита символов, называ-емых «цифрами».
Определение 3. Системой счисления называют систему приемов и правил, позволяющих устано-вить взаимно однозначное соответствие между любым числом и его представлением в виде коне-чного числа символов, называемых «цифрами».
Слайд 3
Понятие системы счисления включает в себя:
• Алфавит, используемый
для записи чисел (цифры, знаки);
• Способ записи чисел;
• Однозначность
представления любого числа.
Системы счисления принято разделять на два класса:
- позиционные;
- непозиционные.
Для позиционных систем счисления значение каждой цифры однозначно определяется ее положением (позицией) в числе.
Для непозиционных систем счисления значение цифры не зависит от ее положения в числе.
Слайд 4
Пример. Римская системы счисления:
LXVI = (66)10 ;
XLIV =
(44)10 .
Два числа состоят из одинаковых цифр (L
= 50, X = 10, V = 5, I = 1), однако имеют разные значения.
Римскую систему счисления нельзя считать классической непозиционной:
VI = 5 + 1 = 6; IV = 5 – 1 = 4.
Для позиционных систем счисления каждая позиция в числе, на которой может находиться цифра, называется разрядом числа. Нумерацию разрядов принято производить влево и вправо от запятой следующим образом:
Слайд 5
Под весом разряда принято понимать количест-венное значение
цифры данного разряда в числе. Фактически, вес разряда представляет
собой множитель, на который умножается цифра этого разряда при получении значения числа.
Слайд 6
Для системы счисления с основанием S вес
i-го разряда определяется в виде:
Vi = Si .
Основание системы
счисления показывает, во сколько раз вес i-ого разряда числа больше веса предыдущего (i-1)- го разряда.
Под основанием системы счисления можно понимать:
• Количество разнообразных цифр, используемых при записи чисел.
• Основание степени для определения веса разряда.
Запись значения основания в любой системе счи-сления имеет вид: S = 10.
Слайд 7
В учебнике «Прикладная теория цифровых автоматов» Савельева А.Я.
доказывается, что оптимальной (с точки зрения затрат оборудования на
представление и хранение чисел) является система счисления с основанием е ≈2,72.
Слайд 8
Представление чисел в ЭВМ
Классификация данных, используемых в ЭВМ
В отношении данных достаточно широко используется термин «аппаратная
поддержка». Принято считать, что данные некоторого типа в определенных форматах являются аппаратно-поддерживаемыми в рамках определенной моде-ли компьютера (процессора), если в системе ко-манд процессора имеются команды для обработки данных этого типа в соответствующих форматах.
Например, в базовой ЭВМ аппаратно поддержи-ваются целые знаковые числа в 16-битном формате.
Слайд 9
Схема в виде дерева классификации
Слайд 10
К основным типам нечисловых данных, обладаю-щих аппаратной поддержкой,
принято относить логические значения и символьные данные.
Для логических значений
характерным свойством является их побитовая обработка, то есть каждый бит логического значения обрабатывается незави-симо от других битов формата. Как правило, от-дельные биты логических значений объединяются в стандартные форматы, которые в терминологии фирмы Intel имеют следующие наименования:
Byte (B) байт – 8 бит;
Word (W) слово – 16 бит;
Double Word (DW) двойное слово– 32 бита;
Quadro Word (QW) учетверенное слово– 64 бита.
Слайд 11
Аппаратная поддержка логических значений реализуется на уровне
логических команд, таких как:
AND – поразрядная конъюнкция (логическое И);
OR
– поразрядная дизъюнкция (логическое ИЛИ);
XOR – исключительное «или» (для двух операндов операция XOR совпадает со сложением по модулю 2);
NOT – инверсия (логическое НЕ).
Символьные данные используются для представления в ЭВМ разнообразной текстовой информации.
Слайд 12
В современных компьютерах для представления символьных данных
используется код ASCII – American Standard Code for Information
Interchange (Американский стандартный код для обмена информацией).
Аппаратная поддержка символьных данных в процессорах Intel 80X86 реализуется на уровне специальных команд обработки строк, основными из которых являются:
MOVS – пересылка строк;
CMPS – сравнение строк;
SCAS – сканирование строки.
Слайд 13
Каждая команда обработки строк рассчитана на обработку одного
элемента строки длиной в байт, слово или двойное слово,
однако использование перед этими командами специального префикса REP (повторение) позволяет осуществлять обра-ботку строки произвольной длины с заданным числом элементов. Использование команд обра-ботки строк с префиксом REP можно рассматри-вать как аппаратную поддержку элементарной структуры данных типа «строка».
Слайд 14
Числовые данные
Аппаратная поддержка числовых данных реали-зуется прежде всего
на уровне арифметических команд, таких как:
ADD – сложение;
SUB – вычитание;
MUL – умножение;
DIV – деление.
Десятичные числа
Десятичные числа используются в ЭВМ на этапе ввода исходных данных или этапе вывода резуль-татов для поддержки удобного интерфейса с поль-зователем.
Слайд 15
В ЭВМ десятичные числа представляются в двоично-кодированной
форме, в связи с чем их часто называют двоично-десятичными
числами.
В современных ЭВМ для кодирования деся-тичных цифр используется код 8421, который характеризуется естественным представле-нием десятичных цифр с помощью двоичной тетрады:
Слайд 16
Десятичные числа принято представлять в ЭВМ в одном
из двух форматов:
•
упакованном (PACK);
• неупакованном (UNPACK).
В упакованном формате в каждом байте числа содержатся две десятичные цифры. Обычно упакованный формат называют BCD-форматом (Binary Coded Decimal).
В неупакованном (распакованном) формате в каждом байте числа представляется только одна десятичная цифра. Типичным примером неупако-ванного формата является представление десятич-ных цифр в коде ASCII.
Слайд 17
В дальнейшем представление десятичных чисел в неупакованном формате
будем называть ASCII-форматом. В данном формате для представления десятичной
цифры отводится младшая тетрада байта (младший полубайт), старшая тетрада байта (старший полубайт) принимает стандартное значение (0011)2 = (3)10.
Пример.
Представить число 90345 в BCD и ASCII- форматах.
Слайд 19
На этапе ввода числовых данных и вывода число-вых
результатов десятичные числа представляются в ASCII-формате. Их преобразование в
BCD-формат может быть реализовано либо на аппаратном, либо на программном уровне.
В системе команд процессоров семейства Intel X86 отсутствуют команды преобразования десятичных чисел из одного формата в другой, значит, это пре-образование можно реализовать на программном уровне.
В любой ЭВМ поддерживаются как двоичные, так и десятичные числа, естественно выглядит реали-зация не только двоичной, но и десятичной ариф-метики для обработки десятичных чисел.
Слайд 20
Из-за разделения двоичных чисел на две формы представления
(с фиксированной запятой и с пла-вающей запятой) практически в
любом компью-тере реализована аппаратная поддержка как целочисленной арифметики (для чисел с фикси-рованной запятой), так и арифметики с плавающей запятой. Так, например, в процессорах Intel наряду с целочисленным АЛУ (ALU) имеется также АЛУ для операций над числами с плавающей запятой, которое входит в состав FPU. Для того, чтобы подчеркнуть целочисленность АЛУ, его аббревиа-туру достаточно часто дополняют буквой I: IALU.
Слайд 21
Двоичная и десятичная арифметики
и области их применения
Для
обработки данных в ЭВМ возможно применение одной из двух
следующих схем:
Слайд 22
Первую схему обработки данных целесообразно применять при сравнительно
небольших объемах перерабатываемых данных и достаточно большом объеме вычислений
(операций), приходящихся на единицу данных. Подобным свойством обладают так называемые научно-технические задачи.
Слайд 23
Вторую схему обработки целесообразно приме-нять при больших объемах
обрабатываемых дан-ных и небольшом объеме вычислений, приходя-щихся на каждую
единицу данных. Подобным свойством обладают так называемые экономические (коммерческие) задачи.
Аппаратная поддержка второй схемы обработки данных в ЭВМ предполагает наличие в составе процессора помимо традиционного двоичного АЛУ еще и десятичного АЛУ. Использование по-добных АЛУ характеризуются ЭВМ, относящиеся к классам Main Frame. В ПК и рабочих станциях на базе практически всех современных процессоров десятичное АЛУ отсутствует.
Слайд 24
Двоичные числа с фиксированной запятой Знаковые и беззнаковые
числа
Основной особенностью представления целых знаковых чисел является использование
допол-нительного кода. Дополнительный код позволяет значительно упростить основные арифметические операции (сложение, вычитание) по сравнению с прямым кодом.
Дополнительный код числа:
X, при X≥0,
[ X ]доп.=
2 n-1 + | X |, при X<0.
Слайд 25
Пример.
n = 5 X = -13
[ X ]пр = 1.1101=24+13=29
[ X ]доп =
25 - |X| = _1.0000 = 1.0011=32-13=19
1.1101
1.0011
Основными форматами, в которых представляются целые числа, являются:
1 байт ;
2 байта – слово;
4 байта – двойное слово;
8 байтов – учетверенное слово.
Слайд 26
Диапазон представления
знаковых целых чисел
-2n-1 ≤ Азн ≤
2n-1-1
1.00…00 0.11…11
n-1 n-1
Отрицательное число по модулю на единицу больше положительного.
Для байтного формата: n = 8
-128 ≤ Азн ≤ 127
Диапазон представления беззнаковых целых чисел
0 ≤ Абзн ≤ 2n – 1
00…0 11…1
n n
Слайд 27
Для байтного формата: n = 8
0 ≤ Азн
≤ 255
Диапазон представления дробных чисел
Для правильной n-разрядной
дроби:
2-n ≤ |Адр| ≤ 1 - 2-n
0.00…01 0.11…1
Неправильная дробь в целой части содержит обязательную и единственную единицу.
1 ≤ |Адр.нпр.| ≤ 2 - 2-(n+1)
1.00…0 1.11…1
Слайд 28
Числа с плавающей запятой
В формате представления
чисел с плавающей запятой имеются три части:
• знак (представляется
крайним левым битом формата)
• мантисса (представляется в виде правильной или неправильной двоичной дроби);
• порядок (представляется в общем случае как целое число со знаком).
С учетом этих частей значение числа с плавающей запятой представляется в виде:
Апз = (-1)signA• MA• SPA
signA – знак; PA – порядок числа;
MA –мантисса числа А; S – основание порядка.
Слайд 29
Основные особенности представления чисел с плавающей запятой в
современных ЭВМ
Классы ЭВМ:
• Универсальные ЭВМ – Mainframe (MF), такие
как: IBM System 370;
Модели ЕС ЭВМ: EC 1010; EC 1065; EC 1087.
• Мини ЭВМ, такие как:
DEC: PDP-11; VAX-11;
Модели CM ЭВМ: СМ 1- СМ 4; СМ 1420,…
• ПК (например, на базе процессоров Intel 80X86, Pentium). Стандарт IEEE 754
Слайд 30
1. Мантисса представляется в прямом коде независимо от
знака числа.
2. Порядок числа представляется со смещением как целое
число без знака. Величина смещения обычно равна весу старшего разряда смещенного порядка или на единицу меньше его.
3. В качестве основания порядка используются:
1. Универсальные ЭВМ – S = 16;
Классы: 2. Мини ЭВМ – S = 2;
3. ПК – S = 2.
4. В целях повышения точности в основном используются нормализованные числа с плавающей запятой.
Слайд 31
Определение. Число с плавающей запятой называется нормализованным, если
старшая цифра его мантиссы является значащей (не 0).
5. Мантисса чисел в классах универсальных ЭВМ и мини ЭВМ является правильной дробью, а в стандарте IEEE – неправильной.
6. Использование в качестве основания порядка S=2 и использования в основном нормализован-ных чисел в мини ЭВМ и ПК требует, чтобы
старшая цифра мантиссы была равна 1. Старшая единица мантиссы с целью увеличения точности в формате не представляется, а лишь подразуме-вается, и называется скрытым разрядом (скрытой единицей).
Слайд 32
7. В целях разумного компромисса между точ-ностью
представления и скоростью обработки данных в ЭВМ используется несколько
форматов:
• короткий формат (формат одинарной точ-ности) - 32 разряда;
• длинный формат (формат двойной точ-ности) – 64 разряда;
• расширенный формат (формат расширенной точности) :
для MF и Мини ЭВМ – 128 разрядов;
для IEEE – 80 разрядов.
В классах MF и Мини ЭВМ увеличивается разряд-ность мантиссы, в стандарте IEEE – и мантиссы и порядка.
Слайд 33
Диапазон представления чисел
с плавающей запятой
Определяется в отношении
модуля нормализо-ванного числа.
MAmin SPAmin ≤ | Aп.т. норм |
≤ MAmax SPAmax
Для классов:
MF
S = 16, d = 64 – смещение порядка.
Характеристика: 0 ≤ XA ≤ 127;
Порядок: -64 ≤ PA ≤ 63.
1/16• 16-64 ≤ | Aп.т. норм | < 1• 1663
Слайд 34
Мини ЭВМ
S = 2; d = 128 –
смещение порядка.
Характеристика: 0 ≤ XA ≤ 225;
Порядок: -128 ≤
PA ≤ 127.
1/2• 2-128 ≤ | Aп.т. норм | < 1• 2127
Cтандарт IEEE
S = 2;
d = 127 – для короткого формата;
d = 1023 – для длинного формата;
d = 16383 – для расширенного формата.
Слайд 35
Скрытая единица имеется только в коротком или длинном
формате, в расширенном формате она представляется в явном виде.
При
определении диапазона представления чисел необходимо учитывать особенности стандарта IEEE-754:
Крайние значение характеристики (порядка) во всех форматах зарезервированы и для представ-ления нормализованных чисел не используются. Максимальное значение характеристики при знаке + и нулевой мантиссе зарезервировано для +∞ и для представления не чисел (NAN).
Слайд 36
Максимальное значение характеристики с едини-цей в старшем разряде
мантиссы используется для представления - ∞.
Минимальное значение характеристики исполь-зуется
для представления ненормализованных чи-сел со знаками +, − и для представления нуля (+0 и -0).
Поэтому диапазон характеристики
для короткого формата: 1 ≤ XA ≤ 254;
диапазон чисел: 2-126 ≤ | Aп.т. норм | < 2128.
для длинного формата: 10-308 ≤ | Aп.т. норм | < 10308.
для расширенного формата:
10-4932 ≤ | Aп.т. норм | < 104932
Слайд 37
Точность представления чисел
Каждая десятичная дробь представляется в
виде бесконечной двоичной дроби, что в условиях ограниченного формата
приводит к возникновению погрешности.
Максимальная абсолютная погрешность имеет место в том случае, когда все отбрасываемые разряды равны единице.
0 . 10 ………110 111 …….1
n n+1 ∞
где n- разрядность числа.
Слайд 38
Погрешность представления чисел с плавающей точкой определяется погрешностью
мантиссы как дробного числа.
Слайд 39
Формула справедлива для правильных и неправильных дробей.
Точность представления
чисел для различных типов машин
ЕС: δАп.т. = 16
• 2-24 = 2-20 = 10-6;
СМ: δАп.т. = 2•2-24 = 2-23 = 10-7;
IEEE: δАп.т. = 10-7.
Методы округления чисел с плавающей точкой
Округление производится для повышения точности представления чисел.
Методы округления оговариваются стандартом IEEE 754.
Слайд 40
• Округление усечением – не вписывающиеся в сетку
разряды отбрасываются;
• Округление к ближайшему – анализируется старший отбрасываемый
разряд, если он равен 1, то к младшему разряду мантиссы добавляется 0;
• Округление к ближайшему большему (округление к + ∞)- для положительных чисел 1 добавляется в младший разряд мантиссы, для отрицательных чисел мантисса не меняется.
• Округление к ближайшему меньшему (округление к -∞) – для отрицательных чисел единица добавляется в младший разряд мантиссы.
Слайд 41
Все методы, кроме метода усечения, позволяют уменьшить максимальную
относительную погрешность. По умолчанию используется метод округления к ближайшему.
Регистр
флагов
Арифметические флаги формируются арифмети-ческими командами и являются признаками их результата.
Флаги управления оказывают влияние на процесс выполнения программ.
К арифметическим флагам относятся:
Слайд 42
• (CF) Carry Flag – флаг переноса, в
нем фиксируется перенос из старшего разряда при сложении и
заем в старший разряд при вычитании. При умножении CF показывает возможность (=0) и невозможность (=1) представления произведения в том же формате, что и операндов.
• (PF) Parity Flag – флаг паритета (четности). Устанавливается в единицу при наличии четного числа единиц в младшем байте результата, в противном случае - сбрасывается.. PF используется в качестве аппаратной поддержки контроля по четности.
Слайд 43
• (AF) Auxiliary Carry Flag - флаг вспомогательного
переноса, в котором фиксируется межтетрадный перенос при сложении и
межтетрадный заем при вычитании. Этот флаг используется командами десятичной арифметики.
• (ZF) Zero Flag – флаг нуля, устанавливается при нулевом значении результата, в противном случае сбрасывается.
• (SF) Sign Flag – флаг знака, в котором копируется старший разряд результата.
Слайд 44
• (OF) Overflow Flag флаг переполнения. Устанавливается в
командах сложения и вычитания, если результат не помещается в
формате, при этом и операнды и результат интерпретируются как знаковые числа. Аппаратно он формируется совпадением переносов из двух старших разрядов при сложении и заемов в два старших разряда при вычитании (если они совпадают, то флаг равен нулю).
Выполнение арифметических операция в ЭВМ
Слайд 45
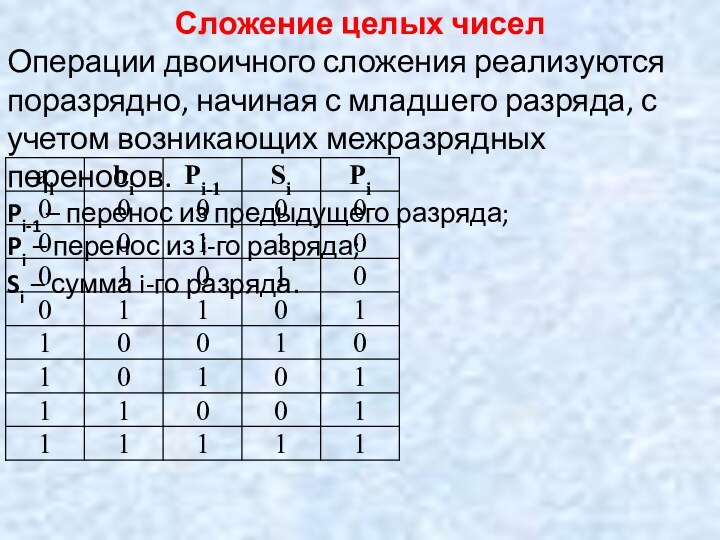
Сложение целых чисел
Операции двоичного сложения реализуются поразрядно, начиная
с младшего разряда, с учетом возникающих межразрядных переносов.
Pi-1 –
перенос из предыдущего разряда;
Pi – перенос из i-го разряда;
Si – сумма i-го разряда.
Слайд 46
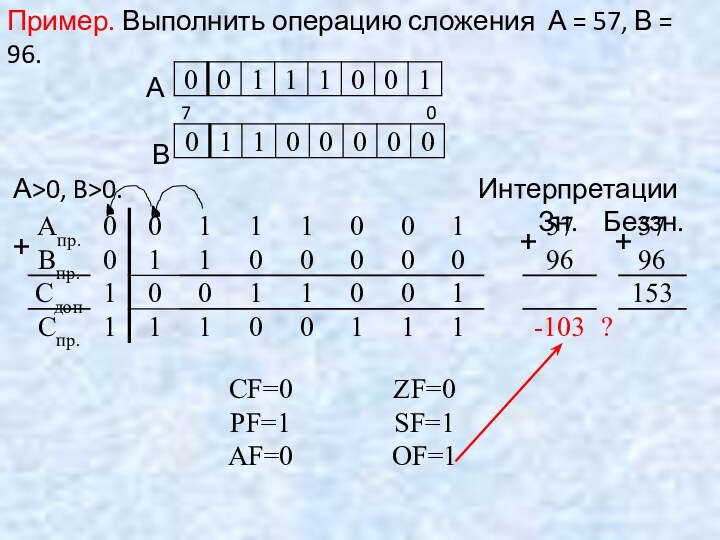
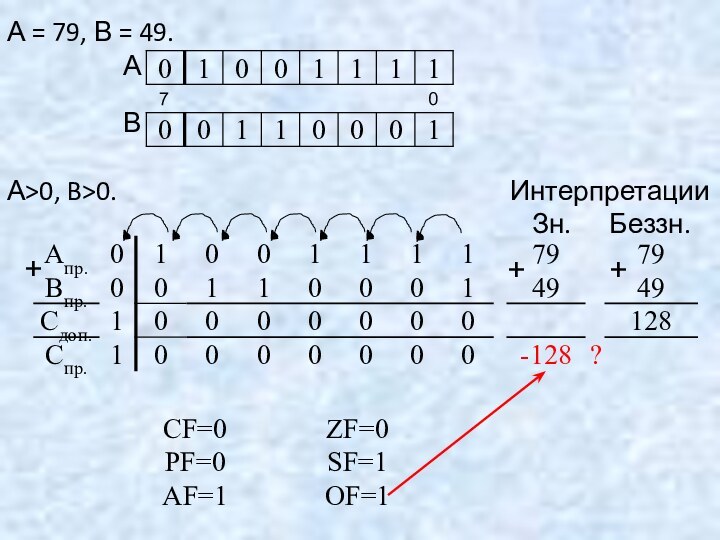
Пример. Выполнить операцию сложения А = 57, В
= 49.
А>0, B>0.
Интерпретации
Знаковая Беззнаковая
+
+
+
Интерпретации
Зн. Беззн.
+
+
+
Интерпретации
Зн. Беззн.
+
+
+
Интерпретации
Зн. Беззн.
+
+
+
Слайд 50
Пример. Выполнить операцию сложения А = 57, В
= 96.
А
В
А>0, B>0. Интерпретации
Зн. Беззн.
7 0
+
+
+
Интерпретации
Зн. Беззн.
+
+
+
А
В
А>0, B>0. Интерпретации
Зн. Беззн.
7 0
+
+
+
Интерпретации
Зн. Беззн.
+
+
+
Слайд 54
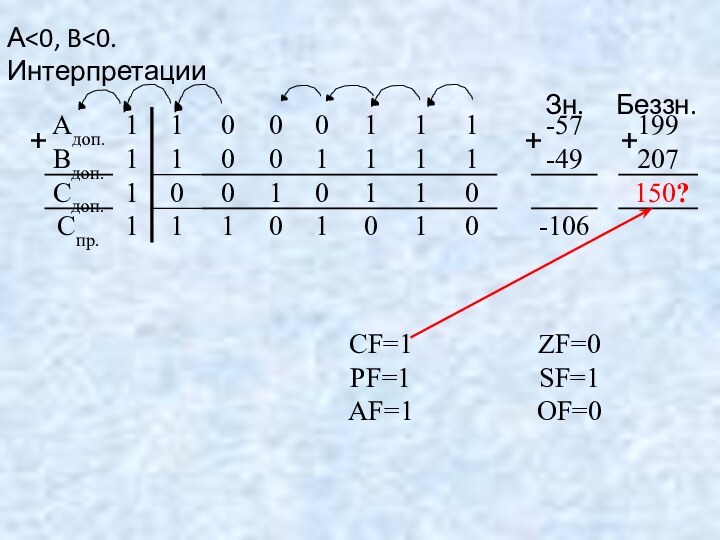
Переполнение при сложении чисел возникает только в том
случае, если операнды имеют одинаковые знаки. Переполнение фиксируется тремя
способами:
• сравнение знаков операндов и суммы: если знак суммы отличается от знаков операндов, то фиксируется переполнение;
• сравнение переносов из двух старших разрядов: если они не совпадают, то фиксируется переполнение;
• использование модифицированного знака (под знак отводится два разряда, второй разряд дублирует знак).
Слайд 55
Вычитание целых чисел (в формате IEEE)
1. Вычитание можно
проводить двумя способами:
Сведение вычитания к сложению, заменяя операнд В
на противоположный.
2. Выполнение прямого (непосредственного) вычитания производится поразрядно, начиная с младших разрядов, с учетом возникающих межразрядных заемов.
Пример.
Для заданных чисел А и В выполнить операцию знакового вычитания со всеми комбинациями знаков операндов.
Слайд 56
Вычитание реализуется по следующей таблице:
Zi-1- заем из i-го
разряда;
ri – разность;
Zi – заем в i-й разряд из
(i-1)-го разряда.
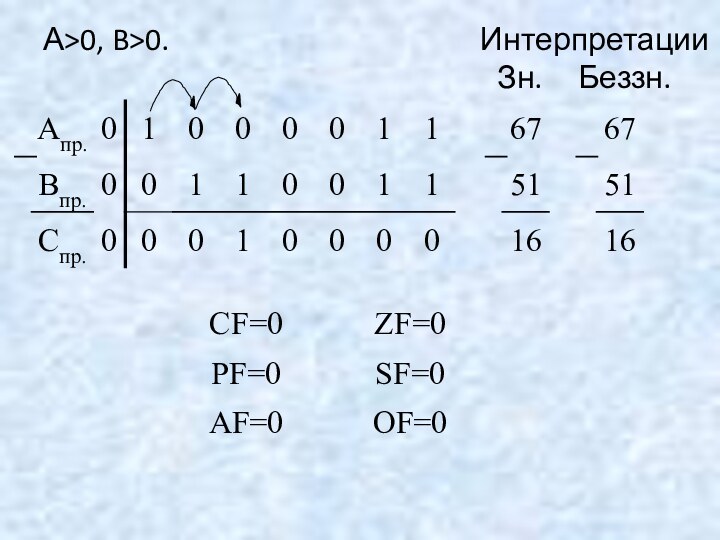
1. А = 67, В = 51.
[А]пр.=0.1000011
[В]пр.=0.0110011
[А]пр.=1.1000011; [А]доп.=1.0111101
[В]пр.=0.0110011
Интерпретации
Зн. Беззн.
Слайд 59
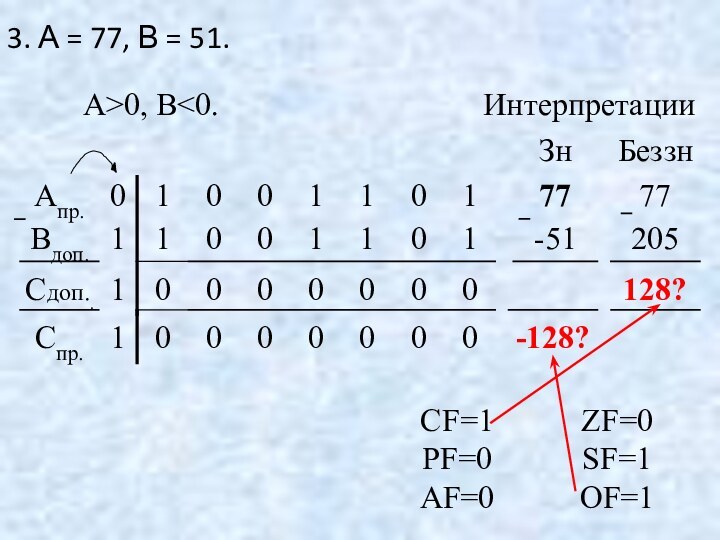
А0.
[А]пр.=1.1000011;
[В]пр.=1.0110011; [В]доп.=1.1001101
Интерпретации
Зн. Беззн.
Слайд 65
Для знакового вычитания переполнение возможно только при разных
знаках операндов.
О переполнении можно судить по одному из
двух признаков:
1. знак результата отличается от знака первого операнда;
2. несовпадение заемов в два старшие разряда (один из них присутствует, а другой нет).
Слайд 66
Операция умножения целых чисел и принципы ее реализации
в ЭВМ
Умножение двоичных чисел состоит в последова-тельном умножении множимого
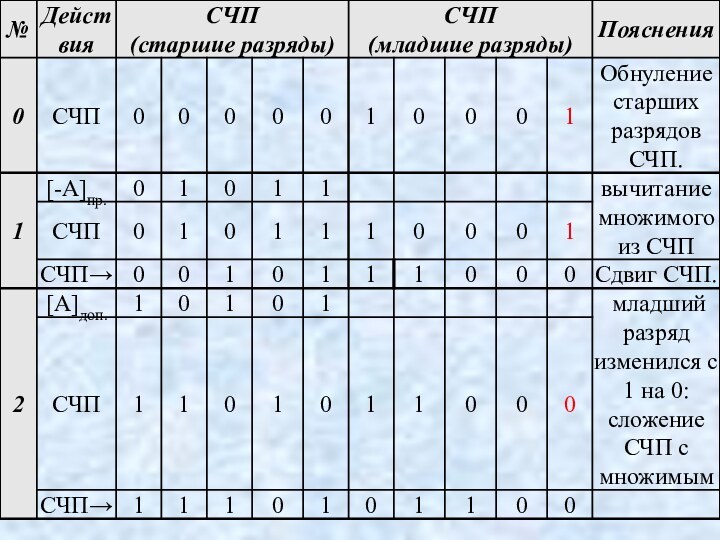
на отдельные раз-ряды множителя с суммированием результатов умножения. Результат умножения множимого на один разряд множителя принято называть частным произведением (СЧП).
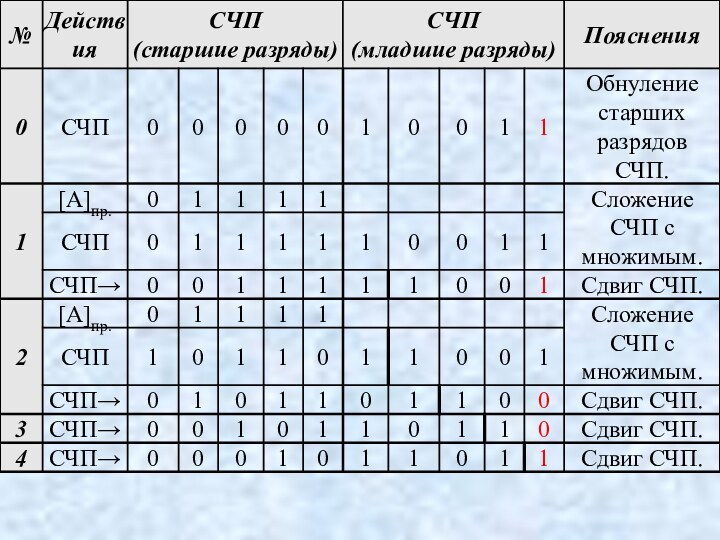
Пример.
А = 13, В = 11.
Слайд 67
Первый способ: 1 1
0 1
1 0 1 1
1 1 0 1
1 1 0 1
1 1 0 1 ______
1 0 0 0 1 1 1 1 (143)10
х
х
Второй способ: 1 1 0 1
1 0 1 1
1 1 0 1
1 1 0 1
1 1 0 1
_________ 1 1 0 1
1 0 0 0 1 1 1 1
Слайд 68
Особенности операций умножения целых чисел:
• каждое частное произведение
либо совпадает с множимым, либо равно нулю;
• формируемые частные
произведения должны быть определенным образом сдвинуты друг отно-сительно друга для их последующего суммирования;
• частное произведение можно формировать, начиная как от младших, так и от старших разрядов множителя;
• для результата умножения требуется количество цифр, равное сумме количества цифр операндов. Если операнды имеют одинаковое количество цифр, то для суммы потребуется 2n разрядов.
Слайд 69
Особенности реализации операций
умножения в ЭВМ:
1. В операционном
устройстве для умножения двоичных чисел должен использоваться многоразрядный двоичный
сумматор, поэтому умножение реализуется в виде последовательного многошагового процесса, на каждом шаге которого проводится умножение на один разряд множителя. Для фиксации суммы частных произведений необходимо использовать 2n-разрядный регистр при n-разрядных операндах. Перед началом операции этот регистр необходимо обнулить;
Слайд 70
2. На каждом шаге умножения анализируется определенный разряд
множителя. Если он равен 1, то на этом шаге
проводится сложение суммы частных произведений с множимым. Если разряд равен 0, то сложение не проводится;
3. Каждый шаг умножения должен сопровождать-ся сдвигом суммы частных произведений (СЧП) от-носительно неподвижного множимого, или наобо-рот: сдвиг множимого относительно неподвижной СЧП;
4. Умножение можно начинать как с младших, так и со старших разрядов множителя;
Слайд 71
5. В целях упрощения схемы умножения регистр множителя
реализуется как сдвигающий, это дает возможность анализировать только один
разряд регистра. При выполнении умножения, начиная от младших разрядов, схема анализа привязывается к младшему разряду регистра множителя, регистр при этом сдвигается вправо;
При реализации умножения, начиная от старших разрядов, схема анализа привязывается к старше-му разряду множителя, реализуется сдвиг вправо.
6. Для фиксации завершения операции в операци-онном устройстве умножения должен быть ис-пользован счетчик (inc или dec), который считает количество разрядов множителя;
Слайд 72
7. Так как возможно умножение, начиная от стар-ших
и с младших разрядов (то есть сдвигается мно-жимое или
СЧП), то можно использовать четыре способа (схемы) умножения.
Способы (схемы) реализации умножения в ЭВМ
• начиная от младших разрядов множителя со сдвигом множимого влево;
• начиная от младших разрядов со сдвигом СЧП вправо;
• начиная от старших разрядов со сдвигом множимого вправо;
• начиная от старших разрядов со сдвигом СЧП влево.
Слайд 73
Анализ схем
1. В схемах умножения со сдвигом множимого
для его представления требуется два n-разрядных регистра.
2. Для схем
умножения со сдвигом СЧП для представления множимого требуется n-разрядный регистр.
3. В схемах умножения, начиная от старших разрядов со сдвигом множителя вправо, необходимо использовать 2n-разрядный регистр.
4. Для схем умножения, начиняя от старших разрядов со сдвигом СЧП влево, требуется 2n-разрядный регистр для хранения суммы СЧП.
Слайд 74
5. Для схем умножения, начиная от младших разрядов
со сдвигом СЧП вправо, требуется n-разрядный регистр.
В целях
экономии оборудования практически во всех ЭВМ реализована схема умножения, начиная от младших разрядов множителя со сдвигом СЧП вправо.
Упрощенная схема операционного устройства для реализации умножения по этому способу представлена на рисунке.
Слайд 76
Умножение чисел с фиксированной запятой
Основные положения
Использование дополнительных кодов
позволяет не переводить отрицательные числа в прямой код и
отрицательный результат в дополнительный код.
Знак умножается так же, как разряды, результат получается в нужном коде.
Умножение в дополнительных кодах с применением коррекции.
Правильный результат получается только при положительных операндах.
С = [Aпр.]×[Bпр.]
Слайд 77
При А0 получаем псевдо-произведение:
С* = [Aдоп.]·[Bпр.] =
[2n - |A|]·[Bпр.] = 2n ·Bпр. - |A| ·Bпр.
Должно
быть: C = 22n - |A| · Bпр
При A>0, B<0: Апр.· [2n - |В|] = 2n · Апр - Апр·|В|
Должно быть: C = 22n - Апр·|В|
При A<0, B<0: (2n - |A|)·(2n - |В|) =
= 22n - 2n·|В| - 2n·|А| + |A| · |В|
Должно быть: C = |A| · |В|
Слайд 78
Два вида коррекции
1. Коррекция окончательного результата состоит в
вычитании множимого из старших разрядов СЧП, которое может быть
заменено на сложение с дополнением множимого. Эта коррекция проводится при отрицательном множителе.
2, При отрицательном множимом коррекция проводится во время умножения и сводится к модифицированному сдвигу СЧП (при сдвиге СЧП вправо в свободный разряд заносится единица).
Примечание. В случае отрицательного множимого (A<0,B>0) при умножении на младшие нули проводится обычный (не модифицированный) сдвиг – в свободный разряд заносится 0.
Слайд 79
Пример. В разрядной сетке длиной в байт (один
разряд знаковый и семь – цифровых) выполнить операцию умножения
заданных чисел А и В со всеми комбинациями знаков, используя метод умножения в дополнительных кодах с применением коррекции. При выполнении операции использовать способ умножения с поразрядным анализом множителя, начиная от его младших разрядов со сдвигом СЧП вправо.
А = 15, В = 13, n = 5.
[Aпр.] = 1.1111 [Bпр.] = 0.1101
[Aдоп.] = 1.0001
а) А<0, B>0:
Слайд 81
Сдоп. = (1.100111101)2
Спр. = (1.011000011)2 = -195
b) А>0,
B
[Bдоп.] = 1.0011
Слайд 83
Спр. = (1.011000011)2 = -195
b) А
1.1111 [Bпр.] = 1.1101
[Aдоп.] =
1.0001 [Bдоп.] = 1.0011
Слайд 85
Спр. = (0.011000011)2 = 195
Умножения в дополнительных кодах
без применения коррекции.
Метод Бута.
Особенности метода.
Сложение или вычитание множимого
на каждом шаге зависит от того, как после сдвига вправо меняется младший разряд множителя.
Слайд 86
Если он поменялся с 0 на 1, то
происходит вычитание множимого из СЧП. При изменении младшего разряда
множителя с 1 на 0 происходит сложение множимого с СЧП.
Если младший разряд множителя не изменился, то производится только сдвиг. При реализации этого метода происходит чередование сложения и вычитания, поэтому старший разряд СЧП в явном виде представляет его знак. При сдвиге знак СЧП сохраняется.
Эффективность метода Бута по сравнению с обычным методом поразрядного умножения проявляется для тех множителей, в которых имеются длинные последовательности единиц.
Слайд 87
Примечание.
При умножении на младшую единицу произво-дится вычитание множимого.
При умножении на младшие нули осуществляется только сдвиг нуле-вой
СЧП и множителя до появления первой единицы.
Пример. А =11, В = 15, n = 5.
[Aпр.] = 0.1011 [Bпр.] = 0.1111
[Aдоп.] = 1.0101 [Вдоп.] = 1.0001
а) А>0, B>0:
Слайд 89
Спр. = (0.010100101)2 = 165
а) А
Слайд 92
Операция целочисленного деления и способы ее реализации в
ЭВМ
Особенности двоичного деления
Пример. А = 130, В = 10.
А/В
= С(R),
где А – делимое,
В – делитель,
С – частное,
R – остаток.
А = (130)10 = (10000010)2
В = (10)10 = (1010)2
0 | 1 0 1 0
1 0
1 0 | 0 1 1 0 1
1 1 1 0 (R<0)
_ 1 0 0 0 0 0 1 0
1 0 1 0
0 0 1 1 0 (R>0)
_ 1 1 0 0 1 0
1 0 1 0
0 0 1 0 (R>0)
_ 0 1 0 1 0
1 0 1 0
1 0 1 1 (R<0)
_ 0 1 0 1 0
1 0 1 0
0 0 0 0 (R≥0)
Слайд 94
Из проделанного примера отчетливо проявляются следующие особенности двоичного
деления:
1) Процесс деления сводится к последовательному вычитанию делителя
первоначально из делимого, а далее – из получаемых текущих остатков (под текущим остатком будем понимать промежуточ-ный результат вычитания делителя из делимого на или очередного остатка на последующих шагах).
2) На начальном шаге делитель совмещается со старшими разрядами делимого, а затем на каждом шаге делитель сдвигается на одну позицию (раз-ряд) вправо относительно неподвижного текущего остатка. На последнем шаге делитель совмещается с младшими разрядами текущего остатка.
Слайд 95
3) Цифры частного, вырабатываемые на каждом шаге, определяются
знаком текущего остатка. Для остатка большего или равного 0
цифра частного равна 1, для остатка, который меньше 0, цифра частного равна 0.
4) О знаке текущего остатка можно судить по наличию или отсутствию заема в старший разряд при вычитании. Если заем есть, то результат вычитания (т.е. текущий остаток) отрицателен. Если заем отсутствует, то результат вычитания и, соответственно, текущий остаток не отрицателен.
Слайд 96
5) При получении отрицательного остатка на очередном шаге
перед переходом к следующему шагу необходимо выполнить восстановление остатка
путем сложения отрицательного остатка с делителем.
Особенности реализации целочисленного деления в ЭВМ
• Т.к. операция деления является обратной по отношению к умножению, а результат сложения n-разрядных сомножителей представляется в 2n-разрядном формате, то делимое по сравнению с делителем так же должно представляться в удвоенном формате.
Слайд 97
• В качестве результата деления формируется не только
частное, но и остаток. Операция деления с остатком должна
удовлетворять следующему соотношению:
B·C + R = A
Для большинства современных процессоров ( в том числе и фирмы Intel) по окончании операции деления частное занимает младшие разряды делимого, а остаток – старшие разряды делимого.
Слайд 98
• В целях экономии оборудования на каждом шаге
операции деления осуществляется не сдвиг дели-теля вправо относительно неподвижного
текущего остатка, а сдвиг текущего остатка влево относи-тельно неподвижного делителя. При этом дели-тель должен совмещаться со старшими разрядами сначала делимого, а на последующих шагах – текущего остатка.
Слайд 99
• Подробный подход к реализации операции деления называется
«метод деления с восстанов-лением остатка». В целях экономии времени
выполнения операции деления в современных процессорах деление реализуется с использов-анием метода без восстановления остатка. Идея метода сводится к тому, что после получения отрицательного остатка на очередном шаге деления осуществляется его сдвиг влево так же, как и для положительного остатка, однако на следующем шаге производится не вычитание делителя из остатка, а сложение делителя с остатком.
Слайд 100
Обоснование метода
Допустим, что на i-ом шаге деления получен
оста-ток Ri
(i+1)-ом шаге над текущим остатком Ri выполняются следующие действия:
а) По методу с восстановлением остатка:
Ri+1 = (Ri + В)·2 – В = 2Ri + 2В – В = 2Ri + В
(Ri + В) – сложение с делителем;
(Ri + В)·2 – сдвиг влево на 1 разряд;
(Ri + В)·2 – В – вычитание делителя.
б) По методу без восстановления остатка:
Ri+1 = 2Ri + В
2Ri – сдвиг отрицательного остатка влево;
2Ri + В – сложение с делителем.
Слайд 101
• При некоторых соотношениях между делимым и делителем
может оказаться, что частное не поме-щается в формат делителя.
Подобная ситуация воз-никает также, если делитель равен 0. Этот особый случай распознается и фиксируется на начальных шагах операции деления. Наличие подобного слу-чая классифицируется как некорректность цело-численного деления и приводит к прерыванию вы-полняемой программы. Выход на это прерывание может быть зафиксирован при попытке разделить двухбайтное делимое, равное 1000, на однобайт-ный делитель, равный 1,2 или 3, при выполнении команды DIV (беззнаковое деление), а при выпол-нении команды IDIV также при В = 4 или 5.
Слайд 102
Деление беззнаковых целых чисел
В основном беззнаковое деление
реализуется по общим принципам, описанным ранее. Это означа-ет, что
цифра частного, вырабатываемая на каж-дом шаге деления, определяется знаком текущего остатка, получаемого на данном шаге. При отрица-тельном остатке вырабатывается цифра частного, равная 0; при положительном остатке – равная 1.
Проверка корректности беззнакового деления
Для n-разрядного делителя и, следовательно, n-разрядного частного условие корректности принимает вид: А/B ≤ 2n – 1 => A/B < 2n
A < B · 2n
A - B · 2n < 0
Слайд 103
Из полученного условия следует, что для проверки корректности
беззнакового деления необходимо произвести вычитание делителя из старших разря-дов
делимого. Если полученная разность отрица-тельна, то деление корректно, т.е. частное поме-щается в формате делителя. Если же результат так называемого «пробного вычитания» положителен или равен 0, то результат деления в виде частного не может быть помещен в n-разрядный формат. При обнаружении такого случая генерируется пре-рывание выполняемой программы по причине не-корректности целочисленного деления. Для про-цессоров Intel это прерывание является стан-дартным, ему присвоен номер, равный нулю.
Слайд 104
Пример беззнакового деления.
А = 141, В =
13, С = 10, R = 11.
Минимальный формат
делителя для выполнения операции n=4.
А = (141)10 = (10001101)2
В = (13)10 = (1101)2
Слайд 106
Пояснения к примеру.
1. Формируемые на каждом шаге (кроме
первого) цифры частного помещаются в освобождающийся при сдвиге влево
младший разряд остатка.
2. Знак остатка определяется наличием или отсут-ствием переноса из старшего разряда при сложе-нии или заема в старший разряд при вычитании. Наличие переноса при сложении свидетельствует о получении положительного остатка, а его отсутствие – о получении отрицательного остатка. В свою очередь наличие заема при вычитании свидетельствует о получении отрицательного остатка, а его отсутствие – о получении положи-тельного остатка.
Слайд 107
3.По результату пробного вычитания на начальном (нулевом) шаге
осуществляется проверка коррек-тности деления, поэтому на данном шаге никакой
цифры частного не формируется.
Пример фиксации некорректности деления.
А = 141, В = 8.
Слайд 108
Для рассматриваемых делимого и делителя С=17.
Аналогичная ситуация фиксации
некорректности деления будет иметь место и при В
том числе и при В=0.
Возможные модернизации метода деления
1. Для явного представления знака остатка можно использовать дополнительный старший бит как в регистре остатка, так и в сумматоре-вычитателе. Следует иметь в виду, что при сдвиге остатка влево может произойти искажение старшего бита остатка, интерпретируемого как знаковый. В связи с этим действия на очередном шаге алгоритма деления следует определять значением знакового бита остатка до сдвига, а не после.
Слайд 109
2. Для упрощения метода операцию вычитания делителя
можно заменить операцией сложения с его дополнительным кодом.
В процессорах
Intel беззнаковое деление реализуется командой DIV, а знаковое - командой IDIV.
Деление знаковых чисел
Аналогично операции умножения знаковое деление может быть реализовано одним из двух методов:
• метод деления в прямых кодах;
• метод деления в дополнительных кодах.
Слайд 110
Основные особенности метода деления
в прямых кодах
1. Отрицательные операнды
предварительно преобразуются из дополнительного кода в прямой.
2. Деление модулей
операндов осуществляется аналогично делению для беззнаковых чисел.
3. Знак частного вырабатывается отдельным действием как сумма по модулю 2 знаковых разрядов операндов.
4. Знаку остатка присваивается знак делимого. Иск-лючением из правил 3,4 является получение нуле-вого частного и(или) нулевого остатка, которым, независимо от знаков операндов, присваивается знак + (положительный ноль).
Слайд 111
5. Отрицательные результаты в конце операции преобразуются из
прямого кода в дополнительный.
6. Существенным отличием знакового деления в
прямых кодах от беззнакового деления является проверка корректности деления, выполняемая на начальных шагах алгоритма.
Обоснование метода проверки
корректности деления
В связи с тем, что старший бит n-разрядного делителя и, соответственно, частного отводится для представления знака, условие корректности для деления модулей операндов имеет вид:
Слайд 112
A| / |В| ≤ 2n-1 – 1 =>
|A| / |В| < 2n-1
|A| / |В| · 2n-1 < 0
Из полученного соотношения следует, что на этапе пробного вычитания следует делимое и делитель расположить друг под другом следующим образом:
2n-1 n n-1 0
|A|
|В| · 2n-1
1 бит
В целях однообразия выполнения пробного вычитания с основным циклом деления, в котором делитель разме-щается под старшими разрядами остатка, необходимо перед выполнением пробного вычитания сдвинуть дели-мое на один разряд влево и после этого произвести вычи-тание делителя из его старших разрядов.
Слайд 113
Основные особенности метода деления в дополнительных кодах
1. Цифры
частного, формируемые на каждом шаге, определяются не только знаком
остатка, но и знаком делителя. При их совпадении цифра частного равна 1, при несовпадении – 0.
2. Действие, выполняемое над текущим остатком на каждом шаге, определяется не только знаком остатка, но и знаком делителя. При их совпадении производится вычитание делителя из старших разрядов остатка, а при несовпадении – сложение делителя со старшими разрядами остатка. Вычитание делителя может заменяться сложением с его дополнительным кодом.
Слайд 114
3. Коррекция остатка выполняется в конце опера-ции (после
выработки всех цифр частного) в том случае, если знак
последнего остатка не совпадает со знаком делимого. Эта коррекция осуществля-ется действием над остатком (прибавление или вычитание делителя), аналогичным действиям в основном цикле деления (определяется сравне-нием знаков остатка и делителя).
4. Коррекция частного выполняется только при отрицательном делимом и нулевом остатке и состоит в инкременте (увеличении на единицу) для положительного частного и декременте для отрицательного частного.
Слайд 115
5. Проверка корректности деления реализуется аналогично методу деления
в прямых кодах только в случае положительных операндов. Для
осталь-ных комбинаций знаков имеют место следующие нюансы:
Обоснование методов проверки корректности
1) А>0, B>0.
A/B < 2n-1 ;
A - B·2n-1 < 0.
2) А<0, B<0.
A/B < 2n-1 ;
A - B·2n-1 > 0.
Слайд 116
Из полученных соотношений следует, что провер-ка корректности при
одинаковых знаках делимо-го и делителя реализуется следующим образом:
а) выполняется
предварительный сдвиг делимого на один разряд влево;
б) из старших разрядов сдвинутого делимого вычитается делитель;
в) знак полученного остатка сравнивается со знаком делимого. Если они совпадают, то деление некорректно, и операция завершается выходом на прерывание. Если знаки делимого и первого остат-ка не совпадают, то формируется старший разряд частного, интерпретируемый как знак, и осущест-вляется переход к основному циклу деления.
Слайд 117
Знак частного формируется по тем же правилам, что
и любая его цифра, т.е. как результат сравнения знаков
текущего остатка и делителя.
3) A<0, B>0.
A/B ≥ - 2n-1;
A/B ≥ - 2n-1 – 1;
A + B·2n-1 + B > 0.
4) A>0, B<0.
A/B > - 2n-1 – 1;
A + B·2n-1 + B < 0.
Из полученных соотношений следует, что провер-ка корректности деления при разных знаках де-лимого и делителя выполняется в такой последо-вательности:
Слайд 118
1. сложение делителя с младшими разрядами делимого;
2. сдвиг
полученного остатка влево;
3. сложение делителя со старшими разрядами остатка;
4.
знак полученного остатка сравнивается со зна-ком делимого. Если они совпадают, то деление некорректно, и операция завершается прерыва-нием. Если знаки делимого и первого остатка не совпадают, то формируется старший разряд част-ного, интерпретируемый как знак, и осуществля-ется переход к основному циклу деления. Знак частного формируется по тем же правилам, что и любая его цифра.
Слайд 119
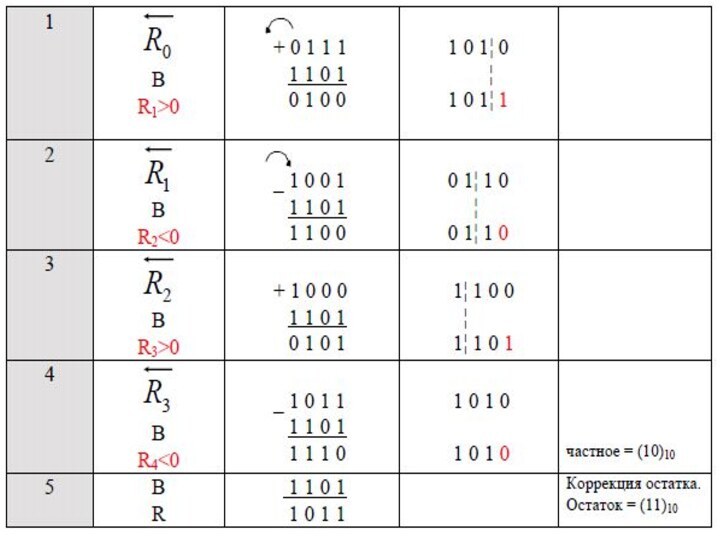
Пример. Выполнить операцию деления заданных чисел А и
В со всеми комбинациями знаков, используя метод деления в
дополнительных кодах. Для представле-ния делимого (А) использовать 16 двоичных разря-дов (один-знаковый,15-цифровых), для представ-ления делителя (В) – 8 разрядов (один-знаковый,7-цифровых). Остаток от деления и частное представляются в той же разрядной сетке, что и делитель.
А = 139, В = 13.
[A]пр. = 0.010001011, [A]доп = 1.101110101;
[В]пр. = 0.1101, [В]доп = 1.0011.
a) A<0; B<0.
Слайд 121
В результате выполнения операции получено положительное частное:
[C]пр =
(0.1010)2 = (+10)10
и отрицательный остаток
[B]доп = (1.0111)2 =
(-9)10,
которые соответствуют значениям:
10·(-13) + 9 = -139.
а) А<0, B>0.
Слайд 123
В результате выполнения операции получено отрицательное частное: [C]доп =
(1.0110)2 = (-10)10
и отрицательный остаток: [B]доп = (1.0111)2 = (-9)10,
соответствующие
значениям: (-10)·13 + (-9) = -139.
Особый случай алгоритма
Такой случай может иметь место только при отри-цательном делимом, нулевом остатке и четном частном. В этом случае получаемый окончатель-ный остаток оказывается не равным нулю, но не подлежит коррекции по общим правилам. Для устранения этого недостатка необходимо модернизировать предлагаемый алгоритм, расширив его на подобные ситуации.
Слайд 124
[А]пр = (-168)10 = (1.0101000)2
[В]пр = (-14)10 =
(1.1110)2
[А]доп = (1.1011000)2
[В]доп = (1.0010)2
Слайд 126
Арифметические операции над числами с плавающей запятой
Операции сложения
и вычитания
Рассмотрим основные нюансы операции сложения на примере для
десятичных чисел.
А = 0, 945 · 103 РА
мантисса МА
В = 0, 847 · 102 РВ
мантисса МВ
Первоначально необходимо привести операнды к одному порядку. Для этой цели мантиссу числа с меньшим порядком сдвигают влево на один разряд (величина разности порядка).
























![Арифметические основы ЭВМ Пример. n = 5 X = -13 [ X ]пр = 1.1101=24+13=29](/img/tmb/15/1465193/bf2ee8565ea70cd8ba257658395e4017-720x.jpg)




























![Арифметические основы ЭВМ А0.[А]пр.=1.1000011; [В]пр.=1.0110011; [В]доп.=1.1001101](/img/tmb/15/1465193/b7f42edcce507fffa3d1f5fe5f6ad099-720x.jpg)
















![Арифметические основы ЭВМ При А0 получаем псевдо-произведение: С* = [Aдоп.]·[Bпр.] = [2n - |A|]·[Bпр.] = 2n](/img/tmb/15/1465193/ff06c48f23beadc0a93fa3a060c9429c-720x.jpg)








































![Арифметические основы ЭВМ В результате выполнения операции получено положительное частное: [C]пр = (0.1010)2 = (+10)10 и отрицательный](/img/tmb/15/1465193/a2234143c786a78c6c384a8703996863-720x.jpg)

![Арифметические основы ЭВМ В результате выполнения операции получено отрицательное частное: [C]доп = (1.0110)2 = (-10)10и отрицательный](/img/tmb/15/1465193/dcf3666f134748d052ed7e103078fb7c-720x.jpg)
![Арифметические основы ЭВМ [А]пр = (-168)10 = (1.0101000)2[В]пр = (-14)10 = (1.1110)2[А]доп = (1.1011000)2](/img/tmb/15/1465193/d6cf996d3a45fff77a8d14c6e8187fd4-720x.jpg)