Презентация на тему Числові методи та моделювання на ЕОМ. Розв’язання системи лінійних рівнянь великої розмірності

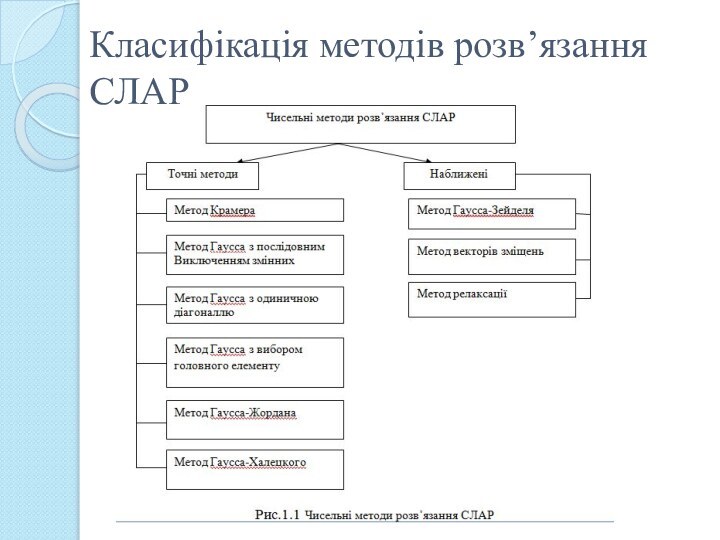
Класифікація методів розв’язання СЛАР на ЕОМ
РОЗДІЛ 2. РОЗВ’ЯЗАННЯ СЛАР

МЕТОДОМ ГАУССА-ЗЕЙДЕЛЯ
2.1. Алгоритм Гаусса-Зейделя
2.2.Умови збіжності ітераційного процесу
2.3. Умови збіжності ітераційного процесу Гаусса-Зейделя
РОЗДІЛ 3. РОЗРОБКА ПРОГРАМНОГО ПРОДУКТУ ДЛЯ РОВ’ЯЗУВАННЯ СЛАР
3.1. Реалізація алгоритму розв’язку СЛАР методом Гаусса-Зейделя в середовищі QT5
3.2. Реалізація алгоритму розв’язку СЛАР методом Гаусса-Зейделя в EXCEL

систем лінійних алгебраїчних рівнянь – одна з основних завдань

обчислювальної лінійної алгебри. Аналітичні методи розв'язання математичних задач, як і раніше, дуже важливі. Чисельні методи суттєво розширюють можливості розв'язання наукових та інженерних задач,адже з ЕОМ ми зменшуємо час та збільшуємо точністю обрахунків.

великої розмірності та класифікація методів їх розв’язання.
Предмет дослідження –

метод Гаусса-Зейделя для вирішення систем лінійних рівнянь великої розмірності точним методом.
Мета дослідження полягає в теоретичному вивченні методів розв’язання СЛАР та практичному використанні набутих знань за допомогою мови програмування C++ в середовищі QT 5.

Гаусса-Зейделя.
Розробити програмний продукт для розв’язання СЛАР методом Гаусса-Зейделя.

належать методи, що дають точний результат у припущенні ідеальної

арифметики. Точні методи можна застосовувати й тоді, коли коефіцієнти й вільні члени рівняння задані в аналітичній, символьній формі.

Ітераційні методи
Ітераційні методи встановлюють процедуру уточнення певного початкового наближення до розв'язку. При виконанні умов збіжності вони дозволяють досягти будь-якої точності просто повторенням ітерацій. Перевага цих методів у тому, що часто вони дозволяють досягти розв'язку з наперед заданою точністю швидше, а також розв'язувати більші системи рівнянь.

збігається, якщо елементи головної діагоналі більше суми модулів елементів

відповідної стрічки крім діагонального елементу цієї стрічки, тобто виконується умова: або умова

QT 5

лінійної алгебри за рішенням СЛАР в програмній інтерпретації на

мові програмування С++ в середовищі QT. Алгоритм програми було перевірино в середовищі Microsoft Excel.
По завершенні роботи були досягнуті необхідні цілі і виконані поставлені завдання.
Було проведено аналіз методів розв'язання систем лінійних рівнянь і сучасних засобів вирішення з виявленням їх характерних особливостей;
Описаний математичний метод, необхідний для вирішення поставленого завдання, визначені вхідні та вихідні дані, розроблено алгоритм реалізації програми;
Описана розробка програми (системні вимоги) і діалог з користувачем, наведено контрольний приклад.