Слайд 2
Примеры деревьев
Генеалогические деревья и организационные диаграммы.
Деревья
используются при анализе электрических цепей, при представлении структур математических
формул.
Деревья используются для организации информации в системах управления базами данных и для представления синтаксических структур в компиляторах программ.
Слайд 3
Будем определять дерево как конечное множество Т, состоящее
из одного или более узлов, таких, что:
имеется один специально
обозначенный узел, называемый корнем данного дерева;
остальные узлы (исключая корень) содержатся в попарно не пересекающихся множествах Т1 , Т2 , … , Тn , каждое из которых в свою очередь является деревом. Деревья Т1 , Т2 , … , Тn называются поддеревьями данного корня.
Это определение является рекурсивным, т.е. мы определили дерево в терминах самих же деревьев.
Слайд 4
Каждый узел дерева является корнем некоторого поддерева, которое
содержится в этом дереве. Число поддеревьев данного узла называется
степенью этого узла. Узел с нулевой степенью называется листом.
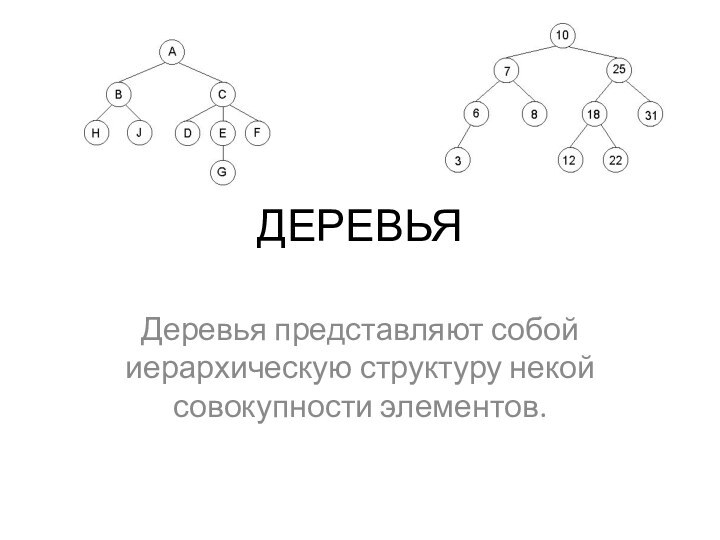
Дерево на рисунке имеет корень A и 5 листьев: H, J, D, G, F. Степени вершин этого дерева следующие: A, В имеют степень 2, С – 3, Е – 1. Корень А располагается на 1 уровне, узлы В, С – на втором, H, J, D, E, F – на третьем, G – на четвертом.
Рис.1
Слайд 5
Бинарное дерево – это дерево, в котором каждый

узел имеет не более двух поддеревьев. В этом случае
будем различать левое и правое поддерево.
Дерево двоичного поиска – это бинарное дерево, узлы которого помечены элементами множества. Определяющее свойство дерева двоичного поиска заключается в том, что все элементы, хранящиеся в узлах левого поддерева любого узла х, меньше элемента, содержащегося в узле х, а все элементы, хранящиеся в узлах правого поддерева узла х, больше элемента, содержащегося в узле х. Это свойство называется характеристическим свойством дерева двоичного поиска и выполняется для любого узла дерева двоичного поиска, включая его корень.
Идеально сбалансированное дерево – это дерево минимальной высоты из элементов некоторого множества, для каждого узла которого будет выполняться условие: модуль разности количеств узлов в любых двух его поддеревьев не превышает единицы. Другими словами дерево называется идеально сбалансированным, если все его уровни, за исключением, может быть, последнего, полностью заполнены.
Слайд 6
Примеры
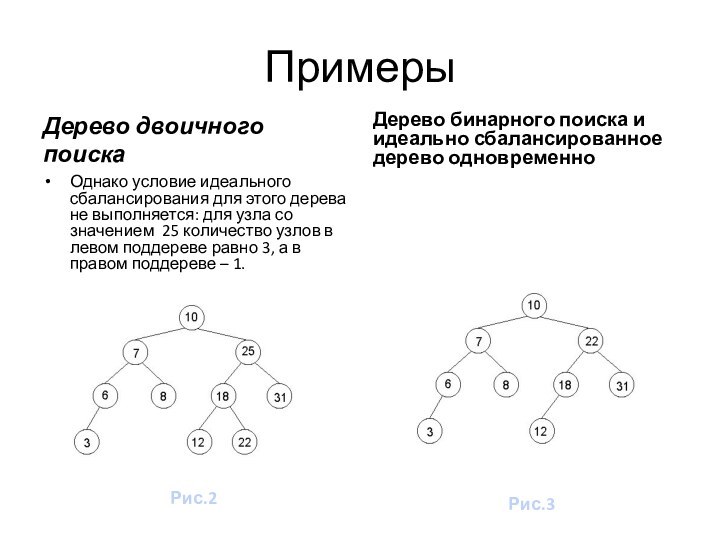
Дерево двоичного поиска
Однако условие идеального сбалансирования для этого
дерева не выполняется: для узла со значением 25 количество
узлов в левом поддереве равно 3, а в правом поддереве – 1.
Дерево бинарного поиска и идеально сбалансированное дерево одновременно
Рис.2
Рис.3
Слайд 7
На C++ бинарное дерево можно представить следующим образом:
struct
tree
{
int inf;
tree *left, *right;
};
tree *root;
В таком представлении
дерево определяется указателем на свой корень. Каждый узел содержит информационную часть (inf) и указатели на узлы, которые являются его левым (left) и правым (right) сыном.
Слайд 8
Обходы бинарных деревьев
Обойти дерево – это побывать в
каждом из его узлов точно по одному разу. Рассмотрим
три наиболее часто используемых способов обхода бинарных деревьев – это обход в прямом, симметричном и обратном порядке. Все три обхода будем определять рекурсивно.
а) Прямой обход:
попасть в корень;
пройти левое поддерево данного корня;
пройти правое поддерево данного корня.
Подпрограмму, составляющую список узлов дерева при прохождении его в прямом порядке, можно записать следующим образом:
void preorder (tree *root)
{
if (root)
{
cout<inf<<"\t";
preorder(root->left);
preorder(root->right);
}
}
Слайд 9
б) Симметричный обход:
пройти левое поддерево данного корня;
попасть в
корень;
пройти правое поддерево данного корня.
Подпрограмму, составляющую список узлов дерева
при прохождении его в симметричном порядке, можно записать следующим образом:
void inorder (tree *root)
{
if (root)
{
inorder(root->left);
cout<inf<<"\t";
inorder(root->right);
}
}
Слайд 10
в) Обратный обход:
пройти левое поддерево данного корня;
пройти правое
поддерево данного корня;
попасть в корень.
Подпрограмму, составляющую список узлов дерева
при прохождении его в обратном порядке, можно записать следующим образом:
void postorder (tree *root)
{
if (root)
{
postorder(root->left);
postorder(root->right);
cout<
inf<<"\t";
}
}
Замечание. Таким образом, при симметричном обходе дерева бинарного поиска на экран выводится упорядоченная по возрастанию последовательность данных. Этот свойство дерева бинарного поиска можно использовать для сортировки данных.
Рассмотрим 3 вида обхода на примере дерева, изображенного на рис.2
При прохождении в прямом порядке список узлов выглядит следующим образом: 10 7 6 3 8 25 18 12 22 31
При прохождении в симметричном порядке список узлов выглядит следующим образом: 3 6 7 8 10 12 18 22 25 31
При прохождении в обратном порядке список узлов выглядит следующим образом: 3 6 8 7 12 22 18 31 25 10
Слайд 11
Операции с деревьями бинарного поиска:
Построение дерева
Рассмотрим подпрограмму
add (int x, tree *&root), которая добавляет новый узел
в дерево так, что бы формировалось дерево бинарного поиска. Она имеет два формальных параметра:
x – информация, которая записывается в новый узел; root – указатель на текущий узел дерева (вначале на корень исходного дерева).
Слайд 12
Построение дерева
бинарного поиска
void add (int x, tree
*&root)
{
if (!root)
{
root = new tree;
root->inf = x;
root->left = root->right = NULL;
}
else if (x < root->inf)
add(x, root->left);
else
if (x > root->inf)
add(x, root->right);
}
Для формирования дерева в основной программе можно написать обращение к этой подпрограмме на этапе ввода в цикле узлы дерева с клавиатуры или считывания их из файла.
Если мы будем вводить с клавиатуры узлы 10, 7, 25, 31, 18, 6, 3, 12, 22, 8, то получим дерево, представленное на рисунке.
Слайд 13
Поиск по дереву
Рассмотрим подпрограмму
search (int x, tree
*root), предназначенную для поиска и вывода данного узла. Подпрограмма
имеет два формальных параметра: x – значение, которое нужно найти; root – указатель на анализируемый узел (вначале root указывает на корень дерева).
Слайд 14
Поиск по дереву
void search (int x, tree *root)
{
if
(!root) coutleft);
else if (x > root->inf) search(x, root->right);
else cout<<"search is successful";
}
Слайд 15
Операции с идеально сбалансированными деревьями
Построение дерева
Рассмотрим
подпрограмму create (int number, tree *&root), которая используется для
формирования идеально сбалансированного дерева.
number – количество узлов в формируемом дереве;
root – указатель на корень дерева.
Необходимо выполнить требование:
для каждого узла количество узлов в левом поддереве отличается от количества узлов в правом поддереве не больше чем на единицу.
Первый узел полагается корнем формируемого дерева, после чего определяется количество узлов в левом поддереве numberLeft = number/2, количество узлов в правом поддереве numberRight = number- numberLeft -1.
Слайд 16
Построение
идеально сбалансированного дерева
void create (int number, tree *&root)
{
int
a;
if (number > 0)
{
root = new
tree;
in >> a; //считываем из файла in очередное число
root->inf = a;
root->left = root->right = NULL;
int numberLeft = number/2, numberRight = number – numberLeft - 1;
create(numberLeft, root->left);
create(numberRight, root->right); }
}