Слайд 2
MSC.Nastran 2001: дискретная оптимизация
Переменные проектирования – величины действительные
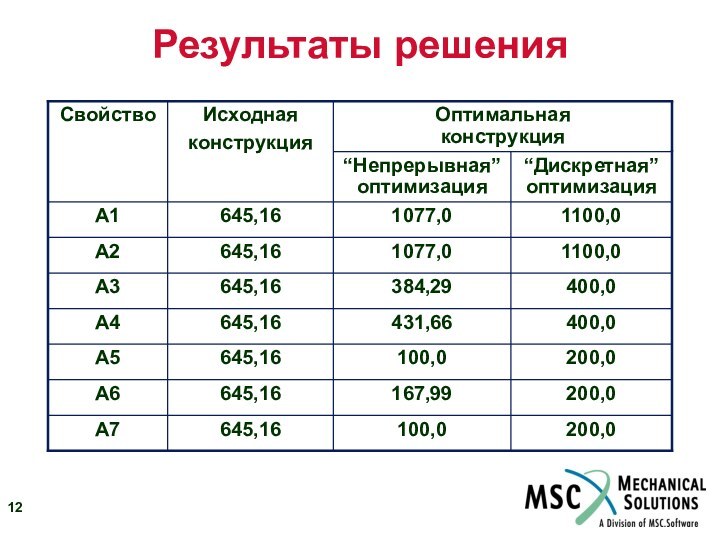
Результаты
решения оптимизационной задачи с помощью MSC.Nastran версий до 2001
– действительные значения с не определенными заранее величинами (в пределах допустимого интервала значений)
Пример:
оптимальное значение толщины i-ой панели ti опт = 1,678 мм
заводской ограничитель: допустимые значения 1,2; 1,5; 2,0; 2,5 мм
MSC.Nastran 2001 решает оптимизационную задачу с учетом требуемой дискретности допустимых значений параметров
Слайд 3
Дискретная оптимизация: управление решением
DESVAR - оператор описания переменной
проектирования
ID – идентификационный номер оператора
LABEL – имя переменной
XINIT –
исходное значение переменной проектирования
XLB – нижняя граница допускаемого значения
XUB – верхняя граница допускаемого значения
DELXV – относительное значение допустимой величины изменения переменной проектирования на одном шаге
DDVAL – идентификационный номер оператора DDVAL, описывающего допустимые дискретные значения переменной
Слайд 4
Дискретная оптимизация: управление решением
DDVAL - оператор задания допустимых
дискретных значений переменной проектирования
ID – идентификационный номер оператора
DVALi
– допустимые дискретные значения
THRU – ключевое слово (обозначает интервал допустимых
значений)
DVAL1 – нижняя граница допускаемого значения
DVAL – верхняя граница допускаемого значения
BY – ключевое слово (обозначает инкремент допустимых
значений)
INC – величина инкремента допустимых значений переменных
Слайд 5
Дискретная оптимизация: управление решением
DOPTPRM - оператор задания параметров
решения задачи оптимизации
DISCOD – идентификатор метода дискретной оптимизации
Vdiscod
– значение параметра DISCOD
DISBEG – номер цикла решения задачи, начиная с которого
выполняется дискретная оптимизация
Vdisbeg – значение параметра DISBEG
Слайд 6
Пример
решения задачи дискретной оптимизации
Оптимизация открытой хвостовой фермы вертолета
(Э.Хог,
Я. Арора. Прикладное оптимальное проектирование. – М.: “Мир”, 1983)
Слайд 7
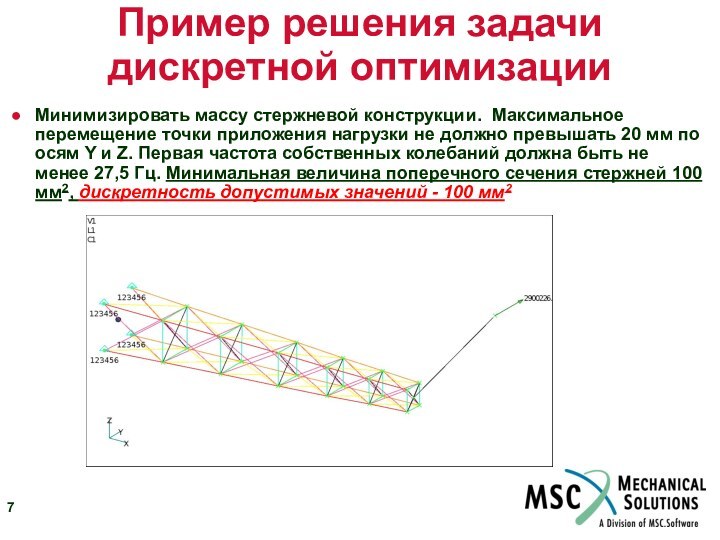
Пример решения задачи дискретной оптимизации
Минимизировать массу стержневой конструкции.
Максимальное перемещение точки приложения нагрузки не должно превышать 20
мм по осям Y и Z. Первая частота собственных колебаний должна быть не менее 27,5 Гц. Минимальная величина поперечного сечения стержней 100 мм2, дискретность допустимых значений - 100 мм2
Слайд 8
Входной файл для решения задачи дискретной оптимизации
SOL 200
TIME
10000
CEND
DESOBJ(MIN) = 101
DESSUB = 201
SPC = 1
SUBCASE 1
ANALYSIS = STATICS
DESSUB = 201
DISPLACEMENT = ALL
STRESS(CORNER) = ALL
LOAD = 1
SUBCASE 2
ANALYSIS = MODES
DESSUB = 501
METHOD = 1
BEGIN BULK
$PARAM,POST,-1
PARAM,AUTOSPC,YES
PARAM,K6ROT,100.
PARAM,MAXRATIO,1.E+8
PARAM,GRDPNT,0
Слайд 9
Входной файл для решения задачи дискретной оптимизации
$***********************************
$ ANALYSIS
MODEL
$***********************************
FORCE,1,30,0,1.,0.,2900226.,0.
EIGRL,1,0.,1000.,5
.
Операторы описания КЭМ (GRID’ы,
CROD’ы, PROD’ы, RBE,
SPC’ы, MAT1)
.
$***********************************
$ DESIGN MODEL
$***********************************
DESVAR, 1,A1,645.16,0.01,1.0E+20, ,1
DESVAR, 2,A2,645.16,0.01,1.0E+20, ,2
DESVAR, 3,A3,645.16,0.01,1.0E+20, ,3
DESVAR, 4,A4,645.16,0.01,1.0E+20, ,4
DESVAR, 5,A5,645.16,0.01,1.0E+20, ,5
DESVAR, 6,A6,645.16,0.01,1.0E+20, ,6
DESVAR, 7,A7,645.16,0.01,1.0E+20, ,7
$
Слайд 10
Входной файл для решения задачи дискретной оптимизации
DDVAL,1,100.,THRU,10000.,BY,100.
DDVAL,2,100.,THRU,10000.,BY,100.
DDVAL,3,100.,THRU,10000.,BY,100.
DDVAL,4,100.,THRU,10000.,BY,100.
DDVAL,5,100.,THRU,10000.,BY,100.
DDVAL,6,100.,THRU,10000.,BY,100.
DDVAL,7,100.,THRU,10000.,BY,100.
$
DVPREL1, 1,PROD,
1, 4,0.01,1.0E+20, , ,+
+, 1,1.0
DVPREL1, 2,PROD, 2, 4,0.01,1.0E+20, ,
,+
+, 2,1.0
DVPREL1, 3,PROD, 3, 4,0.01,1.0E+20, , ,+
+, 3,1.0
DVPREL1, 4,PROD, 4, 4,0.01,1.0E+20, , ,+
+, 4,1.0
DVPREL1, 5,PROD, 5, 4,0.01,1.0E+20, , ,+
+, 5,1.0
DVPREL1, 6,PROD, 6, 4,0.01,1.0E+20, , ,+
+, 6,1.0
DVPREL1, 7,PROD, 7, 4,0.01,1.0E+20, , ,+
+, 7,1.0
$
DRESP1,101,W,WEIGHT
$
Слайд 11
Входной файл для решения задачи дискретной оптимизации
DRESP1,301,Y30,DISP, ,
,2, ,30
DRESP1,302,Z30,DISP, , ,3, ,30
DCONSTR,201,301,-20.,+20.
DCONSTR,201,302,-20.,+20.
$
DRESP1,401,STRESS1,STRESS,PROD, ,2, ,1
DRESP1,402,STRESS2,STRESS,PROD, ,2, ,2
DRESP1,403,STRESS3,STRESS,PROD,
,2, ,3
DRESP1,404,STRESS4,STRESS,PROD, ,2, ,4
DRESP1,405,STRESS5,STRESS,PROD, ,2, ,5
DRESP1,406,STRESS6,STRESS,PROD, ,2, ,6
DRESP1,407,STRESS7,STRESS,PROD, ,2, ,7
DCONSTR,201,401,-2.0E+5,2.0E+5
DCONSTR,201,402,-2.0E+5,2.0E+5
DCONSTR,201,403,-2.0E+5,2.0E+5
DCONSTR,201,404,-2.0E+5,2.0E+5
DCONSTR,201,405,-2.0E+5,2.0E+5
DCONSTR,201,406,-2.0E+5,2.0E+5
DCONSTR,201,407,-2.0E+5,2.0E+5
$
DRESP1,501,E1,EIGN, , ,1
DCONSTR,501,501,30000.,1.0E+6
$
DOPTPRM,IPRINT,0,DESMAX,20,P1,1,P2,15
$
ENDDATA