Презентация на тему Двоичные Б-деревья (ДБД) m=1

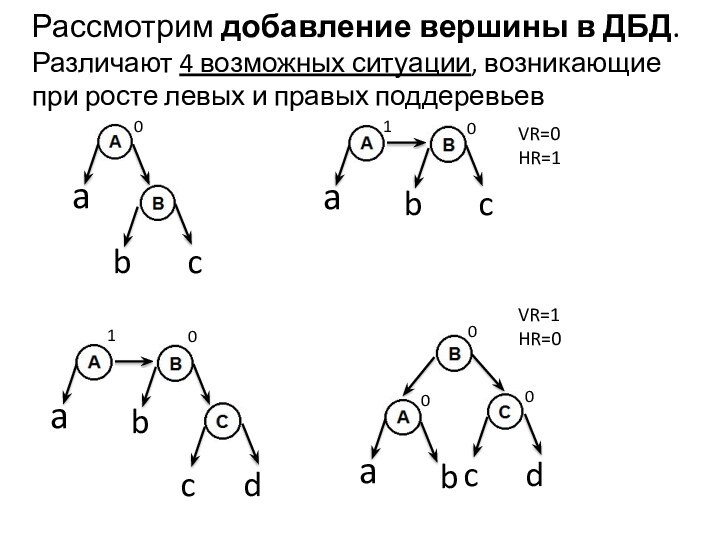
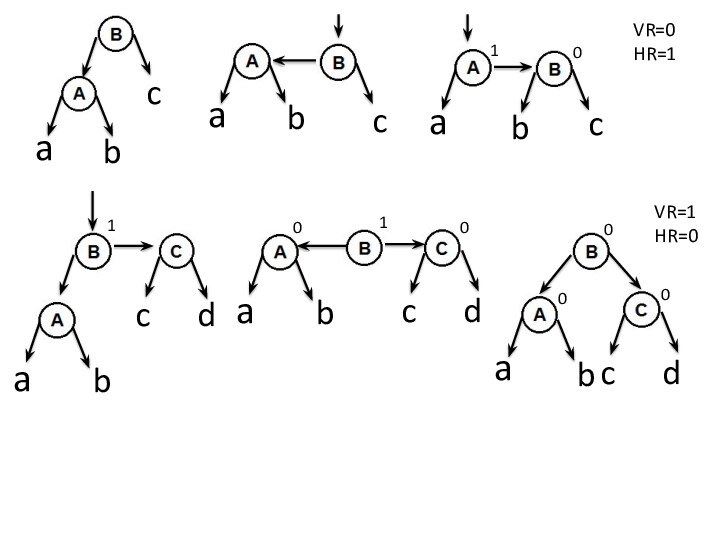
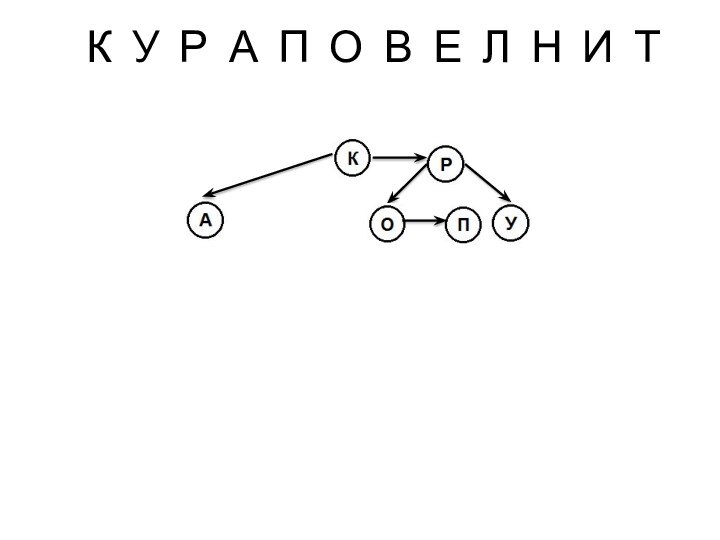
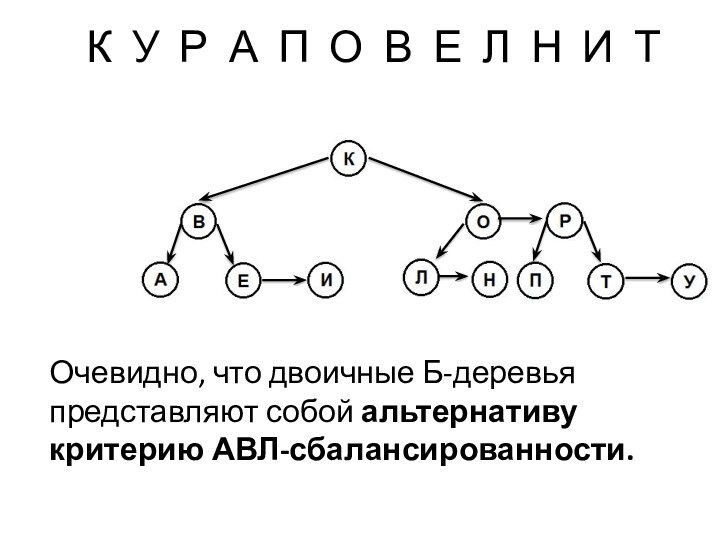
или двумя элементами, страница содержит две или три ссылки

на поддеревья.
Пример: или


Так как имеем дело с оперативной памятью, то необходимо её эффективно использовать. Поэтому представление страницы в виде массива уже не подходит.
Решение – динамическое размещение на основе списочной структуры. Страница - список из одного или двух элементов.

• X •

• X • Y •

a

b

a

b

c

трех потомков (содержать не более трех ссылок), то попытаемся

объединить ссылки на потомков и ссылки внутри страницы (вертикальные и горизонтальные).
Тогда страницы Б-дерева теряют свою целостность. Элементы начинают играть роль вершин в двоичном дереве.

a

b

a

b

c

X

X

Y

следить, чтобы все листья были на одном уровне.
Введем логические

переменные HR и VR – горизонтальный и вертикальный рост дерева.
Показатель баланса Bal = 0 или 1



Bal помещаем в структуру дерева,
переменные HR и VR – глобальные.

a

b

c

X

Y

1

0

ситуации, возникающие при росте левых и правых поддеревьев

) , p-->Data =

D,
p-->Left = p-->Right = NULL, p-->Bal = 0, VR = 1
ELSE IF ( p-->Data > D) B2INSERT(D, p-->Left)
IF ( VR=1 )
IF (p-->Bal=0) q=p-->Left, p-->Left=q-->Right, q-->Right=p,
p=q, q-->Bal=1, VR=0, HR=1
ELSE p-->Bal=0, VR=1, HR=0
FI
ELSE HR=0
FI

IF (VR=1) p-->Bal=1, HR=1, VR=0

ELSE IF (HR=1)
IF(p-->Bal=1) q=p-->Right, p-->Bal=0,
q-->Bal=0, p-->Right=q-->Left,
q-->Left=p, p=q, VR=1, HR=0
ELSE HR=0
FI
FI
FI
FI
FI

Л Н И Т

Л Н И Т
Очевидно, что двоичные Б-деревья представляют

собой альтернативу критерию АВЛ-сбалансированности.