системах счисления
Перевод чисел из одной системы счисления в другую
Системы
счисления используемые в компьютереКонтрольные вопросы
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему История счёта и систем счисления
Содержание
- 2. Содержание:Исторические сведения о системах счисленияСистемы счисленияАрифметические действия
- 3. Счет появился тогда, когда человеку потребовалось информировать
- 4. Самым простым инструментом счета были пальцы на
- 5. Одна из таких систем счета впоследствии и
- 6. В древние времена люди ходили босиком. Поэтому
- 7. Запомнить большие числа было трудно, поэтому к
- 8. Для запоминания чисел использовались камешки, зерна, ракушки и т. д.Содержание
- 9. Потребность в записи чисел появилась в очень
- 10. Археологами найдены такие "записи" при раскопках культурных
- 11. Единичная запись для таких чисел была громоздкой
- 12. Очень наглядной была система таких знаков у
- 13. Как и большинство людей для счета небольшого
- 14. Число 1 245 386 в древнеегипетской записи будет выглядеть1245386Содержание
- 15. В середине V в. до н. э.
- 16. Запись алфавитными символами могла делаться в любом
- 17. Эта форма записи чисел получила большое распространение
- 18. Чтобы различать буквы и цифры, над числами
- 19. Римская нумерацияЭто номера глав в книгах, указание
- 20. Это, самая распространенная на сегодняшний день нумерация,
- 21. В древней Индии и Китае существовали системы
- 22. Из арабского языка заимствовано и слово "цифра"
- 23. Система счисления — совокупность правил наименования и
- 24. Сегодня мы настолько сроднились с 10-ной системой
- 25. Системы счисления Непозиционные ПозиционныеСистемы счисления, в которых
- 26. В римской записи числа важно не собственное
- 27. Наиболее совершенными являются позиционные системы счисления, т.е.
- 28. Любая позиционная система счисления характеризуется своим основаниемОснование
- 29. Приняв за основание число 10, получаем знакомую
- 30. Приняв за основание число 2, получаем двоичную
- 31. Приняв за основание число 8, получаем восьмеричную
- 32. Приняв за основание число 16, получаем шестнадцатеричную
- 33. Арифметические операции выполняются в любой системе счисления
- 34. 1102 100112
- 35. 1102 Х 112 +
- 36. Позиция цифры в числе называется разрядом. В
- 37. Теперь запишем двоичное число, которое может состоять
- 38. При переводе из одной системы счисления в
- 39. Перевод числа из десятичной системы в
- 40. Возьмем десятичное число, например, 1310 и переведем
- 41. Теперь возьмем десятичное число, например, 6910 и
- 42. Возьмем то же десятичное число 6910 и
- 43. Рассмотрим еще перевод десятичного числа 16910
- 44. ВосьмеричнаяСистемы счисления, используемые в компьютереДвоичнаяШестнадцатеричнаяДвоичная система счисления является основной системой представления информации в памяти компьютера.0,10,1,2,3,4,5,6,70,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
- 45. Почему люди пользуются десятичной системой, а компьютеры
- 46. Почему в компьютерах используются также восьмеричная и
- 47. Скачать презентацию
- 48. Похожие презентации
Содержание:Исторические сведения о системах счисленияСистемы счисленияАрифметические действия в системах счисленияПеревод чисел из одной системы счисления в другуюСистемы счисления используемые в компьютереКонтрольные вопросы
Слайд 2
Содержание:
Исторические сведения о системах счисления
Системы счисления
Арифметические действия в
системах счисления
счисления используемые в компьютереКонтрольные вопросы
Слайд 3 Счет появился тогда, когда человеку потребовалось информировать своих
сородичей о количестве обнаруженных им предметов.
Сначала люди просто
различали один предмет перед ними или нет.
Если предмет был не один, то говорили «много». Первыми понятиями математики были "меньше", "больше" и "столько же". Если одно племя меняло пойманных рыб на сделанные людьми другого племени каменные ножи, не нужно было считать, сколько принесли рыб и сколько ножей. Достаточно было положить рядом с каждой рыбой по ножу, чтобы обмен между племенами состоялся.
Содержание
Слайд 4 Самым простым инструментом счета были пальцы на руках
человека
С их помощью можно было считать до 5, а
если взять две руки, то и до 10.
Содержание
Слайд 5 Одна из таких систем счета впоследствии и стала
общеупотребительной -
десятичная. Содержание
Слайд 6 В древние времена люди ходили босиком. Поэтому они
могли пользоваться для счета пальцами как рук, так и
ног. Таким образом они могли, казалось бы, считать лишь до двадцати.Но с помощью этой «босоногой машины» люди могли достигать значительно больших чисел,
1 человек - это 20,
2 человека - это два раза по 20 и т.д.
До сих пор существуют в Полинезии племена, которые для счета используют с 20-ую систему счисления
Содержание
Слайд 7 Запомнить большие числа было трудно, поэтому к «счетной
машине» рук и ног добавляли механические приспособления.
Например, перуанцы
употребляли для запоминания чисел разноцветные шнуры с завязанными на них узлами. Содержание
Слайд 9 Потребность в записи чисел появилась в очень древние
времена, как только люди научились считать. Количество предметов изображалось
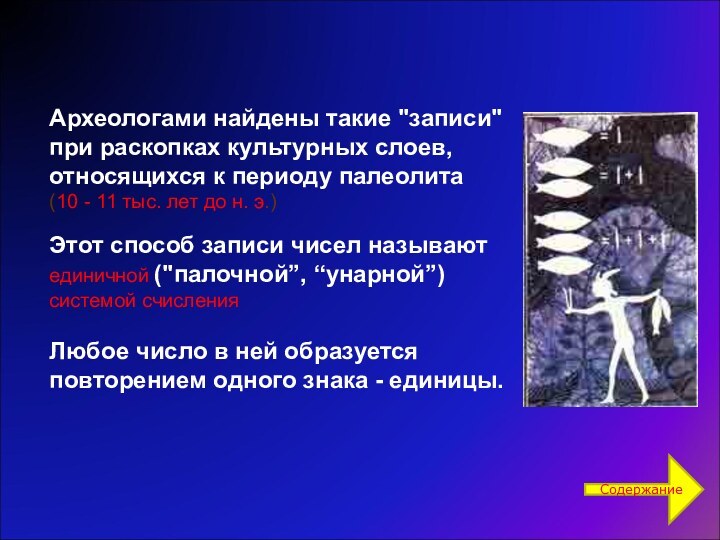
нанесением черточек или засечек на какой-либо твердой поверхности: камне, глине и т.д.Люди рисовали палочки на стенах и делали зарубки на костях животных или ветках деревьев
Содержание
Слайд 10 Археологами найдены такие "записи" при раскопках культурных слоев,
относящихся к периоду палеолита (10 - 11 тыс. лет
до н. э.)Этот способ записи чисел называют единичной ("палочной”, “унарной”) системой счисления
Любое число в ней образуется повторением одного знака - единицы.
Содержание
Слайд 11 Единичная запись для таких чисел была громоздкой и неудобной,
поэтому люди стали искать более компактные способы обозначать большие
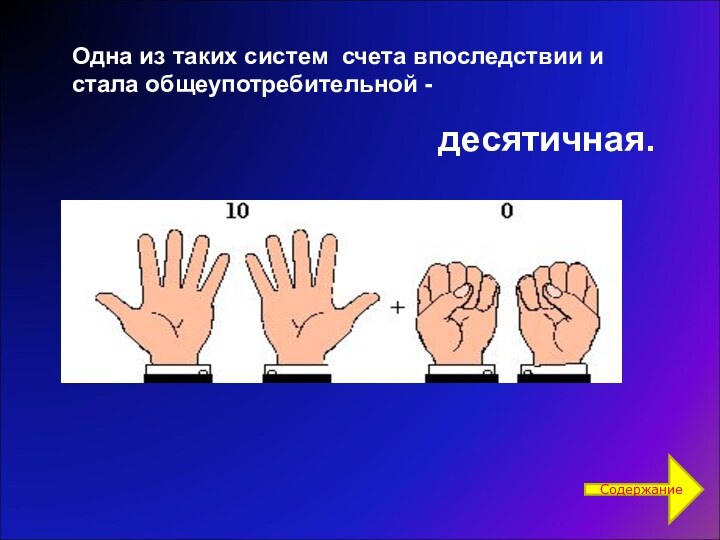
числа.Появились специальные обозначения для «пятерок», «десяток», «сотен» и т.д.
Чем больше зерна собирали люди со своих полей, чем многочисленнее становились их стада, тем большие числа становились им нужны.
Содержание
Слайд 12
Очень наглядной была система таких знаков у египтян.
Египтяне придумали эту систему около 5 000 лет тому назад.
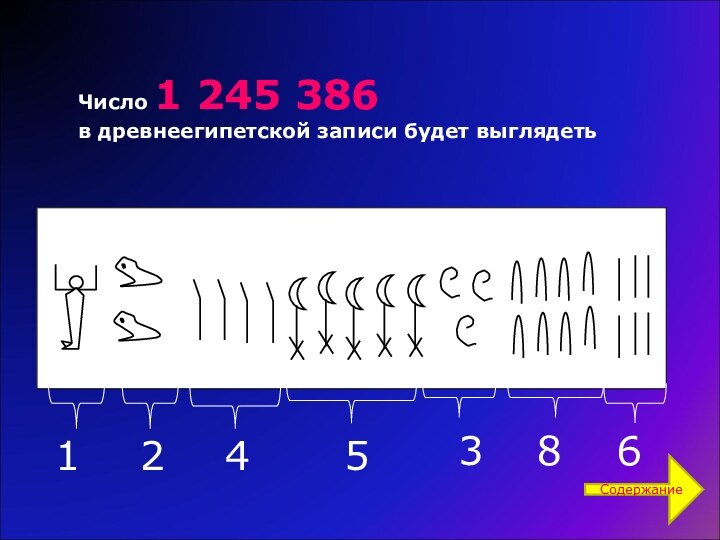
Это одна из древнейших систем записи чисел, известная человекуЕгипетская
нумерация
Содержание
Слайд 13 Как и большинство людей для счета небольшого количества
предметов Египтяне использовали палочки
Каждая единица изображалась отдельной палочкой
Такими
путами египтяне связывали коров
Если нужно изобразить несколько десятков, то иероглиф повторяли нужное количество раз.
Тоже самое относится и к остальным иероглифам.
1
10
Это мерная веревка, которой измеряли земельные участки после разлива Нила.
100
1000
Цветок лотоса
Египетская нумерация
Головастик
100000
1000000
10000000
Египтяне поклонялись богу Ра, богу Солнца и, наверное, так изображали самое большое свое число
Увидев такое число, обычный человек очень удивится и возденет руки к небу
1000
Поднятый палец - будь внимателен
Содержание
Слайд 15 В середине V в. до н. э. появилась
запись чисел нового типа, так называемая алфавитная нумерация.
Алфавитная
нумерацияВ этой системе записи числа обозначались при помощи букв алфавита., над которыми ставились черточки: первые девять букв обозначали числа от 1 до 9, следующие девять - числа 10, 20, 30, ..., 90, и следующие девять - числа 100, 200, ..., 900.
Таким образом, можно было обозначать любое число до 999.
Содержание
Слайд 16 Запись алфавитными символами могла делаться в любом порядке,
так как число получалось как сумма значений отдельных букв.
Например, записи – ϕλβ βϕλ ϕβλ все эквивалентны и означают число 532. Однако выполнять арифметические вычисления в такой системе было настолько трудно, что без применения каких-то приспособлений оказалось обойтись практически невозможно
500 - ϕ
- λ
2 - β
λ β
500 30 2
β ϕ λ
2 500 30
ϕ β λ
500 2 30
Древнегреческая нумерация
90
Содержание
Слайд 17 Эта форма записи чисел получила большое распространение в
связи с тем, что имела полное сходство с греческой
записью чисел. Если посмотреть внимательно, то увидим, что после "а" идет буква "в", а не "б" как следует по славянскому алфавиту, то есть используются только буквы, которые есть в греческом алфавите.
Алфавитная система была принята и в Древней Руси.
Славянская кириллическая нумерация
Содержание
Слайд 18 Чтобы различать буквы и цифры, над числами ставился
особый значок — титло ( ~ ).
До XVII
века эта форма записи чисел была официальной на территории России, Белоруссии, Украины, Болгарии, Венгрии, Сербии и Хорватии.
До сих пор православные церковные книги используют эту нумерацию. Так можно было записывать числа до 999.
Для больших чисел использовался знак тысяч ≠, который ставился впереди символа, обозначавшего число
Содержание
Слайд 19
Римская нумерация
Это номера глав в книгах, указание века,
числа на циферблате часов, и т. д. Возникла эта нумерация
в древнем Риме. В ней имеются узловые числа: один, пять и т. д.Остальные числа получались путем прибавления или вычитания одних узловых чисел из других
Это нумерация, известная нам и в настоящее время.
С нею мы достаточно часто сталкиваемся в повседневной жизни.
Например,
четыре записывается как IV, т. е. пять минус один,
восемь — VIII (пять плюс три),
сорок—XL (пятьдесят минус десять),
девяносто шесть—XCVI (сто минус десять плюс пять и плюс еще один) и т. д.
Содержание
Слайд 20 Это, самая распространенная на сегодняшний день нумерация, которой
мы пользуемся в настоящее время.
Применяемые в настоящее время цифры
1234567890 сложились в Индии около 400 г.н.э Арабы стали пользоваться подобной нумерацией около 800 г.н.э., а примерно в 1200 г.н.э. ее начали применять в Европе, однако в Европе они стали известны благодаря трудам арабских математиков, и потому за ними утвердилось название «арабские», хотя сами арабы вплоть до настоящего времени пользуются совсем другими символами.
Арабские цифры:
В России арабская нумерация стала использоваться при Петре I (до конца XVII века сохранилась славянская нумерация)
Арабская нумерация
Содержание
Слайд 21 В древней Индии и Китае существовали системы записи,
построенные на МУЛЬТИПЛИКАТИВНОМ ПРИНЦИПЕ. В таких системах для записи
одинакового числа единиц, десятков, сотен или тысяч применяются одни и те же символы, но после каждого символа пишется название соответствующего разряда.Если десятки обозначить символом Д,
а сотни - С, то число 325 будет выглядеть
так : 3С2Д5.
Индийцы и соединили греческие принципы нумерации со своей десятичной мультипликативной системой.
Содержание
Слайд 22
Из арабского языка заимствовано и слово "цифра"
(по-арабски
"сыфр"), означающее буквально "пустое место"
Это слово применялось
для названия знака пустого разряда, и этот смысл сохраняло до XVIII века, хотя еще в XV веке появился латинский термин "нуль" (nullum - ничто).
Форма индийских цифр претерпевала многообразные изменения.
Та форма, которой мы сейчас пользуемся установилась в XVI веке. По мнению марроканского историка Абделькари Боунжира арабским цифрам в их первоначальном варианте было придано значение в строгом соответствии с числом углов, которые образуют фигуры
Содержание
Слайд 23 Система счисления — совокупность правил наименования и изображения
чисел с помощью набора символов, называемых цифрами.
Количество цифр
(знаков), используемых для представления чисел называют
Основанием системы счисленияСодержание
Слайд 24 Сегодня мы настолько сроднились с 10-ной системой счисления,
в которой десять цифр.
Так что не представляем себе иных
способов счета.Но до наших дней сохранились следы счета шестидесятками. Такой системой счисления пользовались в Древнем Вавилоне.
Ведь до сих пор мы делим час на 60 минут, а минуту на 60 секунд. Окружность делят на 360, то есть 6*60 градусов, градус - на 60 минут, а минуту - на шестьдесят секунд.
в сутках 24 часа, а в году 365 дней. Таким образом,
время (часы и минуты) мы считаем в 60-ной системе,
сутки - в 24-ной,
недели в 7-ной,
Содержание
Слайд 25
Системы счисления
Непозиционные
Позиционные
Системы счисления, в которых каждой
цифре соответствует величина, не зависящая от её места в
записи числаСистемы счисления, в которых вклад каждой цифры в величину числа зависит от её положения (позиции) в последовательности цифр, изображающей число
Древнегреческая, кириллическая, римская
Десятичная, двоичная и т.д.
Содержание
Слайд 26 В римской записи числа важно не собственное положение
цифры, а где она стоит относительно другой цифры:
записи XII и IX. Здесь в обоих случаях цифра "I" стоит на 2-ом месте справа,но в одном случае ее нужно прибавлять к 10, а в другом вычитать!
Содержание
Слайд 27 Наиболее совершенными являются позиционные системы счисления, т.е. системы
записи чисел, в которых вклад каждой цифры в величину
числа зависит от её положения (позиции) в последовательности цифр, изображающей числоНапример, в числе 53 цифра "5" в разряде десятков дает числу вклад в 50 единиц (5*10).
Позиционные системы счисления результат длительного исторического развития непозиционных систем счисления
Содержание
Слайд 28
Любая позиционная система счисления характеризуется своим основанием
Основание позиционной
системы счисления – это количество различных знаков или символов,
используемых для изображения цифр в данной системе счисления.За основание системы счисления можно принять любое натуральное число – два, три, четыре и т. д.
В разные исторические периоды многие народы пользовались системами счисления отличными от десяти.
Так, например, довольно широкое распространение имела двенадцатеричная система. В устной речи остатки этой системы сохранились, когда мы вместо 12 употребляем “дюжина”. У англичан оно осталось – 1 фут=12 дюймам,
1 шиллинг=12 пенсам.
Содержание
Слайд 29 Приняв за основание число 10, получаем знакомую нам
десятичную систему счисления:
0, 1,
2, 3, 4, 5, 6, 7, 8, 9Всего 10 разных знаков составляют алфавит десятичной системы счисления. Можно записать любое число включая все эти знаки: 237, 12840, 987, 23...
Основание системы счисления обозначают буквой q.
Для десятичной системы счисления q=10
Содержание
0123456789
Слайд 30 Приняв за основание число 2, получаем двоичную систему
счисления:
0, 1
Всего 2
разных знака составляют алфавит двоичной системы счисления.Можно записать любое число включая эти знаки: 1, 11, 101, 110, 10010011… - обратите внимание: используем только цифры от 0 до 1.
Для двоичной системы счисления q=2
Содержание
01
Слайд 31 Приняв за основание число 8, получаем восьмеричную систему
счисления:
0, 1, 2, 3, 4,
5, 6, 7Всего 8 разных знаков составляют алфавит восьмеричной системы счисления
Можно записать любое число включая все эти знаки:237, 145, 32, 12765… - обратите внимание: используем цифры от 0 до 7
Для восьмеричной системы счисления q=8
Содержание
01234567
Слайд 32 Приняв за основание число 16, получаем шестнадцатеричную систему
счисления. Здесь мы можем воспользоваться 10 знаками десятичной системы,
добавив еще 6 знаков – буквы латинского алфавита (A, B, C, D, E, F): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F10 11 12 13 14 15
Всего 16 разных знаков составляют алфавит шестнадцатеричной системы счисления.
Можно записать любое число включая все эти знаки: А37, 1В45, F302, 1A3C5… - обратите внимание: используем знаки от 0 до F.
Для шестнадцатеричной системы счисления q=16
Содержание
0123456789ABCDEF
Слайд 33 Арифметические операции выполняются в любой системе счисления по
одним и тем же правилам.
СЛОЖЕНИЕ. ДВОИЧНЫХ ЧИСЕЛ
Сложение много разрядных
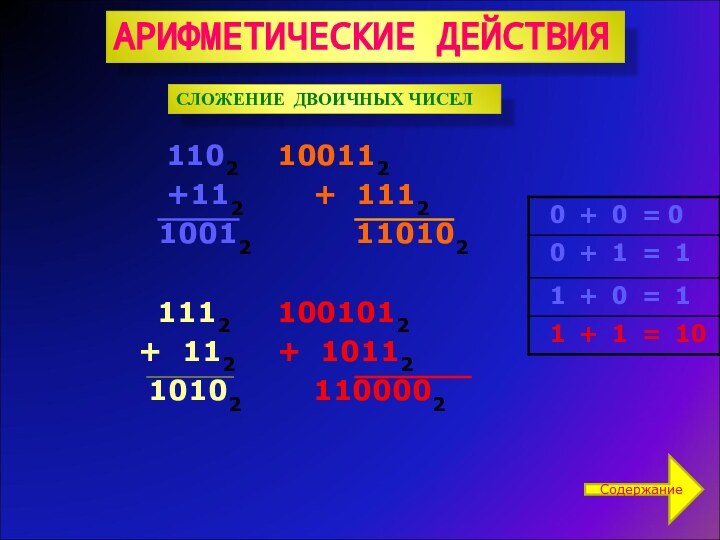
чисел в двоичной системе счисления происходит согласно данной таблице с учетом переноса в старший разряд.АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ
Содержание
Слайд 34
1102 100112
+112 + 1112
10012
1101021112 1001012
+ 112 + 10112
10102 1100002
СЛОЖЕНИЕ ДВОИЧНЫХ ЧИСЕЛ
АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ
Содержание
Слайд 36 Позиция цифры в числе называется разрядом. В записи
правый разряд – разряд единиц, затем смещаясь влево -
десятки, сотни, тысячи и так далее.Число 555 записано в привычной для нас свернутой форме. Мы настолько привыкли к такой записи, что уже не замечаем, как в уме умножаем цифры числа на разные степени числа 10. Это число в развернутой форме будет выглядеть так :
55510 = 5 · 102 + 5 · 101 + 5 · 100 ,
откуда видно, что число в позиционной системе записывается в виде суммы числового ряда степеней основания ( в нашем случае это 10), в качестве коэффициентов которых выступают цифры данного числа.
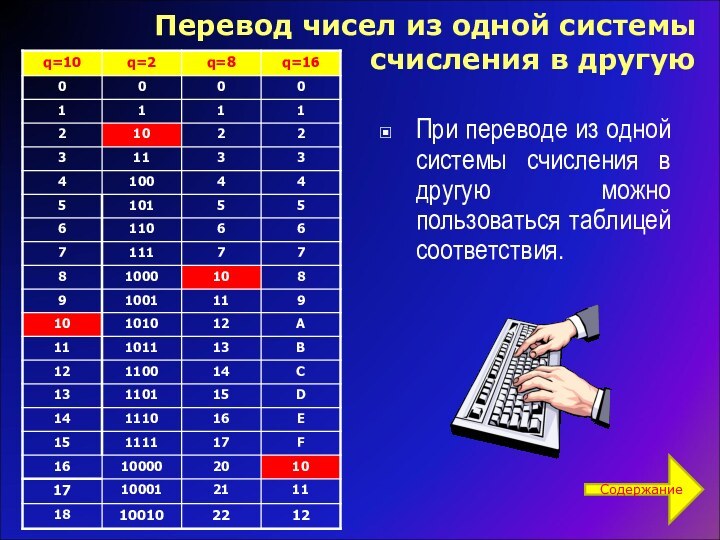
q=10
Содержание
Слайд 37 Теперь запишем двоичное число, которое может состоять только
из нулей и единиц, например, 11112 в развернутом виде:
11112 = 1 · 23 + 1 · 22 + 1 · 21 + 1 · 20 .q=2
Теперь запишем восьмеричное число, которое может состоять из цифр от 0 до 7, например, 24518 в развернутом виде:
24518 = 2 · 83 + 4 · 82 + 5 · 81 + 1 · 80
Рассмотрим развернутую запись числа представленного в шестнадцатеричной системы счисления:
А23С16 = А · 163 + 2 · 162 + 3 · 161 +С · 160
Где цифра А= 10, С=12.
q=8
q=16
ПЕРЕВОД чисел в десятичную систему счисления выполнить довольно легко. Для этого необходимо записать число в развернутой форме и вычислить его значение в десятичном виде.
Содержание
Слайд 38 При переводе из одной системы счисления в другую
можно пользоваться таблицей соответствия.
Содержание
Перевод чисел из одной системы счисления
в другуюСлайд 39 Перевод числа из десятичной системы в систему
счисления c другим основанием:
Последовательно выполнять деление исходного целого
числа на основание той системы, в которую переводим, пока не получится частное меньшее делителя.Записать полученные остатки в обратном порядке, начиная с последнего частного.
Просмотрим исполнение данного алгоритма на практике:
ПЕРЕВОД ЧИСЕЛ из десятичной системы
q=10
q=2
q=3
q=7
q=8
q=18
Содержание
Слайд 40
Возьмем десятичное число, например, 1310 и
переведем его
в двоичное, выполняя деление на основание: 2
q=10
в
q=2
Ответ читаем по остаткам - наоборот!
Получили что 1310 = 11012
Проверка:
11012= 1 · 23 + 1 · 22 + 0 · 21 + 1 · 20 = 8 + 4 + 0 + 1 = 1310
Итак, перевод из десятичной системы в любую другую происходит путем деления исходного числа на основание той системы, в которую переводим.
Содержание
Слайд 41 Теперь возьмем десятичное число, например, 6910 и переведем
его в восьмеричное, выполняя деление на основание: 8
Ответ читаем по остаткам - наоборот!
Получили: 6910 = 1058
Проверка:
2 1 0
1058= 1 · 82 + 0 · 81 + 5 · 80 =64 + 0 + 5 = 6910
q=10
в
q=8
Содержание
Слайд 42 Возьмем то же десятичное число 6910 и переведем
его в шестнадцатеричное, только теперь выполняя деление на основание:
16Ответ читаем по остаткам - наоборот!
Получили 6910 = 4516
Проверка:
1 0
4516= 4 · 161 + 5 · 160 =64 + 5 = 6910
q=10
в
q=16
Содержание
Слайд 43 Рассмотрим еще перевод десятичного числа 16910
в шестнадцатеричное, выполняя деление на основание: 16
-Последнее частное не делится на 16, и мы заменяем его согласно алфавиту 16-ричной системы на символ А : Получили 16910 = А916
Выполнив проверку убеждаемся в правильности перевода:
1 0
А916= А · 161 + 9 · 160 = 10 · 16 + 9 = 16910 -
Перевод из десятичной системы в любую другую происходит путем деления исходного числа на основание той системы, в которую переводим.
q=10
в
q=16
Слайд 44
Восьмеричная
Системы счисления, используемые в компьютере
Двоичная
Шестнадцатеричная
Двоичная система счисления является
основной системой представления информации
в памяти компьютера.
0,1
0,1,2,3,4,5,6,7
0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
Слайд 45 Почему люди пользуются десятичной системой, а компьютеры —
двоичной?
Компьютеры используют двоичную систему потому, что она имеет ряд
преимуществ перед другими системами: - для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной
- представление информации посредством только двух состояний надежно и помехоустойчиво;
- двоичная арифметика намного проще десятичной.
Недостаток двоичной системы —
быстрый рост числа разрядов, необходимых для записи чисел.
Содержание
Слайд 46 Почему в компьютерах используются также восьмеричная и шестнадцатеричная
системы счисления?
Двоичная система, удобная для компьютеров, для человека неудобна
из-за ее громоздкости и непривычной записи. Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина.
Для программистов удобнее работать с более компактной записью.
Такими системами и являются 8-аяи 16-ая
10000000001 - двоичная 10000000001
1
0
0
2
1
0
4
восьмеричная
шестнадцатеричная
Содержание
