- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Логические основы построения компьютера
Содержание
- 2. Цель.1. Познакомить учащихся с логическими основами компьютера.2.
- 3. Содержание.1. Историческая справка.2. Булева алгебра.3Логические выражения. 3.1
- 4. Историческая справка. Немецкий ученый
- 5. Буль изобрёл своеобразную алгебру
- 6. Булева алгебра.Булева алгебра состоит из компонентов:
- 7. Логические выражения1.Логические
- 8. 1. Логические утверждения – это конкретные частные
- 9. 2. Предикаты – это логические высказывания, значения
- 10. Логическое отрицание. Логическое отрицание или
- 11. Логическое сложение. Логическое сложение или Дизъюнкция, определяет
- 12. Логическое умножение. Логическое
- 13. Логическое следование. Логическое следование
- 14. Эквивалентность. Эквивалентность или Равнозначность.Определяет
- 15. Порядок выполнения логических операций.1. Инверсия - ┐2.
- 16. Построение таблиц. Рассмотрим пример
- 17. При добавлении третьего аргумента
- 18. Существует закономерность: для любого числа N аргументов
- 19. Построим таблицу сложного логического
- 20. Основные законы логики.1.Отсутствие степеней и коэффициентов (идемпотентность):
- 21. 7. Дистрибутивность (распределение): Умножения-(А۷В) ٨ С =
- 22. б) Отрицание вариантов: ¬ (А۷В) = ¬А ٨¬Ва) Отрицание одновременной истинности:¬(А٨В)= ¬А۷¬В
- 23. Скачать презентацию
- 24. Похожие презентации




















Слайд 2
Цель.
1. Познакомить учащихся с логическими основами компьютера.
2. Ввести
понятия логических выражений.
Слайд 3
Содержание.
1. Историческая справка.
2. Булева алгебра.
3Логические выражения.
3.1
Логическое отрицание.
3.2 Логическое сложение.
3.3 Логическое умножение.
3.4
Логическое следование.3.5 Эквивалентность.
4.Построение таблиц.
5.Основные законы логики.
Слайд 4
Историческая справка.
Немецкий ученый Лейбниц
первым (в 1666 году) попытался перевести законы мышления (формальную
логику) из словесного царства, полного неопределенностей, в царство математики, где отношения между объектами или высказываниями определяются в виде математических соотношений.Спустя более ста лет, в 1816 году, уже после смерти Лейбница среди ученых шел разговор о создании логического универсального языка, подчиняющегося строгим математическим законам. В 1847 году Буль написал важную статью на тему «Математический анализ логики», а в 1854 году развил свои идеи в работе «Исследование законов мышления».
Слайд 5 Буль изобрёл своеобразную алгебру –
систему обозначений и правил, применимую ко всевозможным объектам, от
чисел и букв до предложений. Его именем она теперь и называется: алгебра Буля, или булева алгебра.
Слайд 6
Булева алгебра.
Булева алгебра состоит из компонентов:
Логические объекты ( выражения)
Операции над логическими объектамиАксиомы и теоремы, регламентирующие эти
операции
Слайд 8 1. Логические утверждения – это конкретные частные утверждения,
заведомо истинные или ложные, иначе говоря, это логические константы.
Например:
2*2 = 4 ( истина)Волга впадает в Чёрное море. (ложь)
Слайд 9 2. Предикаты – это логические высказывания, значения которых
могут меняться в зависимости от входящих в них переменных
величин, иначе говоря, это логические переменые.Например: А +В >С (принимают значения Истина или Ложь в зависимости от значений А, В, С)
Слайд 10
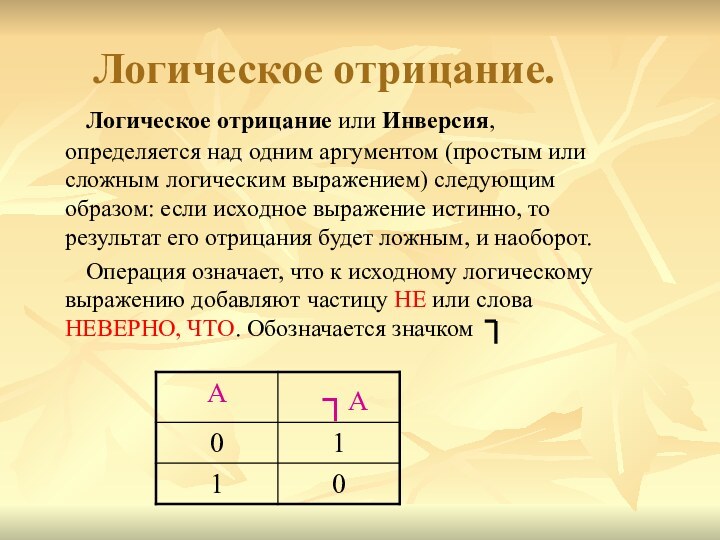
Логическое отрицание.
Логическое отрицание или Инверсия,
определяется над одним аргументом (простым или сложным логическим выражением)
следующим образом: если исходное выражение истинно, то результат его отрицания будет ложным, и наоборот.Операция означает, что к исходному логическому выражению добавляют частицу НЕ или слова НЕВЕРНО, ЧТО. Обозначается значком
Слайд 11
Логическое сложение.
Логическое сложение или Дизъюнкция, определяет логическое
соединение двух логических выражений (высказываний) с помощью союза ИЛИ.
Обозначается значкомСложное логическое выражение будет истинным тогда и только тогда, когда истинно хотя бы одно из исходных (простых) логических выражений.
۷
☺
запомни знак!
Пример: для сдачи экзамена
необходимы знания или везение.
Слайд 12
Логическое умножение.
Логическое умножение
или Конъюнкция, определяет соединение двух логических выражений (высказываний) с
помощью союза И. Обозначается значком & или ٨.Эта операция ставит в соответствие двум простым логическим выражениям новое- сложное, которое будет истинным тогда и только тогда, когда истинны оба исходных (простых) логических выражения.
Запомни знак!
Пример: Учитель должен быть умным и терпеливым (только одновременное наличие двух качеств, ума и терпения, делает выражение истинным).
Слайд 13
Логическое следование.
Логическое следование или
Импликация.
Эта операция связывает два простых логических выражения, из
которых первое является условием, а второе- следствием из этого условия. Выражается словами ЕСЛИ…, ТО… Обозначается значком Результатом импликации является ложь тогда и только тогда, когда (А) истинно, а следствие (В) ложно.
Например: Если выучишь материал, то сдашь зачет (высказывание ложно только тогда, когда материал выучен, а зачет не сдан, ведь сдать зачет можно и случайно, например если попался единственный знакомый вопрос или удалось воспользоваться шпаргалкой.
Слайд 14
Эквивалентность.
Эквивалентность или Равнозначность.
Определяет результат
сравнения двух простых логических выражений А и В, обозначается
значкомРезультат – новое логическое выражение, которое является истинным тогда и только тогда, когда оба исходных выражения одновременно истинны или ложны.
Пример: Когда в зимний день светит солнце и «кусает» мороз, это значит, что атмосферное давление высокое.
Слайд 15
Порядок выполнения логических операций.
1. Инверсия - ┐
2. Конъюнкция
- & или ٨
3. Дизъюнкция – ۷
4. Импликация –
5. Эквивалентность -
Для изменения указанного порядка выполнения логических операций используются круглые скобки.
Например: D = ┐( A ۷ B ٨ C)
Слайд 16
Построение таблиц.
Рассмотрим пример построения
таблицы истинности для следующегося сложного (составного) логического выражения.
D = ┐A ٨ (B ۷ C)Сначала нужно установить число строк и столбцов такой таблицы, то есть спланировать форму таблицы. При определении числа строк необходимо некоторым образом перебрать все возможные сочетания логических значений 0 и 1 исходных выражений А, В и С, из которых формируется заданное сложное логическое выражение.
Слайд 17 При добавлении третьего аргумента сначала
запишем первые 4 строки таблицы, сочетания их со значением
третьего аргумента, равным 0, а затем ещё раз запишем эти же 4 строки, но теперь уже со значением третьего аргумента, равным 1. В результате в таблице для трех аргументов окажется 8 строк (+ девятая строка – шапка таблицы), и при таком подходе легко проверить, что мы действительно не повторили и не пропустили ни одного возможного сочетания логических значений аргументов – исходных выражений А, В, С
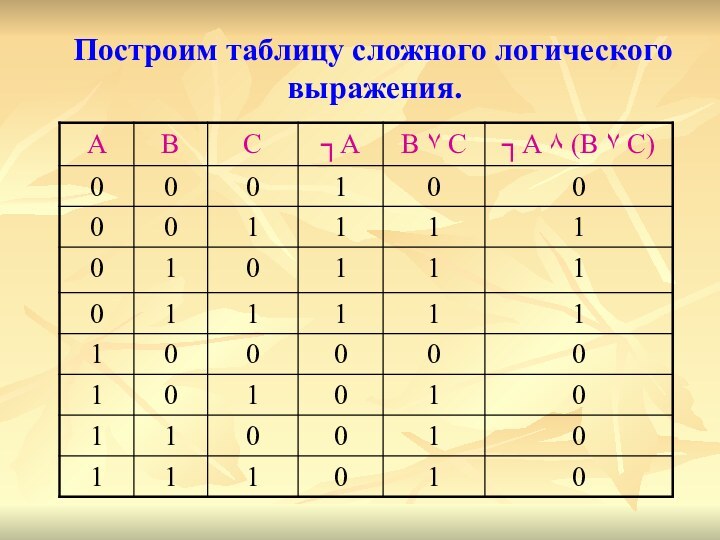
Слайд 18
Существует закономерность:
для любого числа N аргументов сложного
логического выражения таблица истинности содержит 2n строк, а также
строку заголовка (шапка таблицы).Количество столбцов таблицы истинности для её построения выбирают равным М. Эти столбцы соответствуют значениям исходных выражений А, В, С, промежуточных результатов ┐А, (В ۷ С), а также искомого окончательного результата- значения сложного арифметического выражения
┐А ٨ (В ۷ С)
Слайд 20
Основные законы логики.
1.Отсутствие степеней и коэффициентов (идемпотентность): А
٨ А= А; А ۷ А= А
2.Двойное отрицание (инволюция):
¬(¬А) = А3.Закон исключения третьего: А۷¬ А=1(всегда истина)
4.Закон противоречия: А ٨ ¬ А= 0 (всегда ложь)
5.Независимость от перестановки мест (коммутативность): А۷ В= В ۷ А; А ٨ В = В ٨ А
6. Независимость от порядка выполнения однотипных действий (ассоциативность):
(А۷В) ۷ С = А ۷ (В۷С); (А٨В) ٨ С = А ٨ (В٨С).
Слайд 21
7. Дистрибутивность (распределение): Умножения-
(А۷В) ٨ С = (А٨С)
۷ (В٨С) и наоборот:
(А٨В) ۷ (В٨С) = В
٨ (А۷С).Сложения- А۷В٨С = (А۷В) ٨ (А۷С).
8. Законы де Моргана:
а) Отрицание одновременной истинности:¬(А٨В)= ¬А۷¬В
б) Отрицание вариантов: ¬ (А۷В) = ¬А ٨¬В