Слайд 2
Алгоритмические модели
Алгоритмические модели основаны на понятии алгоритма.
Исторически первые точные определения алгоритма, возникшие в 30-х годах,
были связаны с понятием вычислимости. С тех пор было предложено множество, как выяснилось, эквивалентных определений алгоритма.
Чтобы оценить возможности использования алгоритмов для представления неформальных процедур, рассмотрим простую задачу.
ЗАДАЧА. Описать процедуру, реализующую преобразование из именительного падежа в родительный для существительных следующих типов: ДОМ, МАМА, ВИЛКА, КИНО, НОЧЬ, ТОКАРЬ, КИЛЬ.
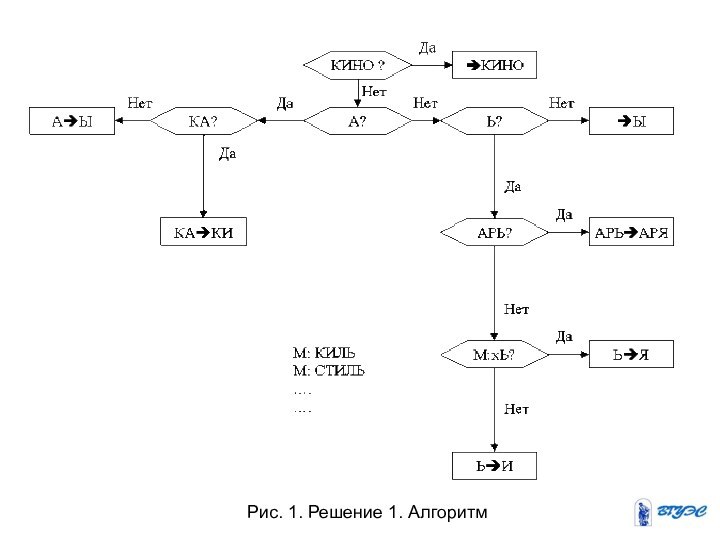
Решение 1 указано на Рис. 1 в виде блок схемы соответствующего алгоритма.
Слайд 3
Рис. 1. Решение 1. Алгоритм
Слайд 4
С точки зрения программирования на алгоритмических языках достоинства
подобного представления очевидны — эта блок-схема без затруднений переводится
в текст программы, например, на языке Ассемблера или С++.
Однако само составление подобной блок-схемы при появлении существительных новых типов становится, очевидно, все более и более утомительным занятием. Для иллюстрации этого предположим, что дана
ДОПОЛНИТЕЛЬНАЯ ЗАДАЧА. Расширить алгоритм, представленный на Рис. 1 на слова ВАСЯ, ВРЕМЯ, АКЦИЯ, ЗАДАЧА
Разумеется программист без особого труда составит соответствующую блок-схему алгоритма. И все же, если учесть, что подобные изменения и расширения алгоритма при программировании неформальных процедур происходят многократно (реальная сложность неформальной процедуры как раз и проявляется в практической невозможности предусмотреть заранее все случаи), следует признать, что, вполне правильное в статике, решение 1 в динамике неудачно!
Слайд 5
Продукционные модели
В подобных случаях для обеспечения динамичности
процессов модификации программ используются те или иные варианты таблиц
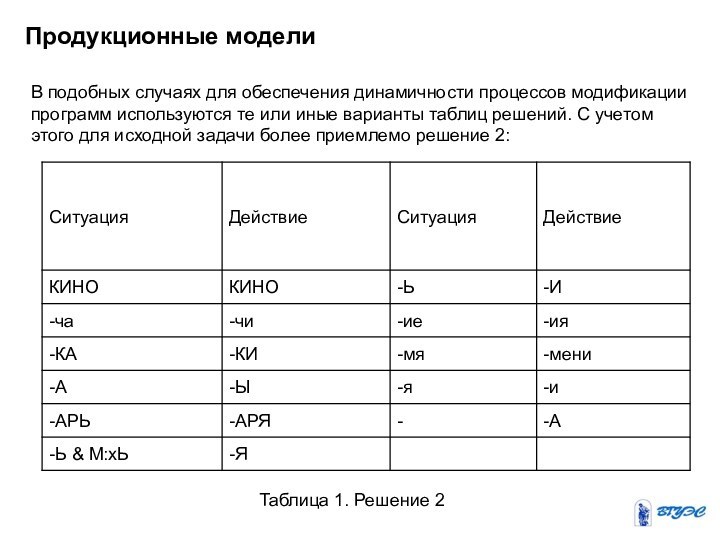
решений. С учетом этого для исходной задачи более приемлемо решение 2:
Таблица 1. Решение 2
Слайд 6
Соответствующая таблица решений содержит две графы — слева
приведены описания ситуаций, справа — соответствующие действия.
Предполагается, что
программист разработал интерпретирующую программу для подобных таблиц. Эта программа работает следующим образом.
Для конкретного входного слова, пусть это будет для примера слово РОЗА,
осуществляется последовательный просмотр ситуаций, указанных в таблице, и сравнение их со входным словом.
Если слово соответствует некоторой ситуации, то выполняется действие, указанное для этой ситуации.
Для слова РОЗА будет обнаружено соответствие с ситуацией "-А". В результате выполнения действия "-Ы" будет получено выходное слово РОЗЫ.
Слайд 7
Теперь значительно упрощается расширение на новые классы слов
— необходимо лишь обеспечить внесение вставок на нужное место
в таблице решений.
Таблицы решений представляют собой частный случай так называемых продукционных систем.
В этих системах правила вычислений представляются в виде продукций. Продукции представляют собой операторы специального вида и состоят из двух основных частей, для краткости называемых обычно "ситуация — действие".
"Ситуация" содержит описание ситуации, в которой применима продукция. Это описание задается в виде условий, называемых посылками продукции.
"Действие" — это набор инструкций, подлежащих выполнению в случае применимости продукции.
Слайд 8
Режим возвратов
Таблица решений, приведенная в Таблице 1,
иллюстрирует так называемую безвозвратную процедуру.
В этом случае на
каждом шаге выбирается единственное решение — так, для слова РОЗА таким решением будет РОЗЫ — проблема выбора решения не возникает.
В общем случае неформальные процедуры являются многозначными, а правильность конкретного выбора, сделанного на некотором шаге, проверяется на следующих шагах. При этом используется так называемый режим возвратов.
а). МАТЬ ——————> ЛЮБИТ ——————> ?
что делать? кого?
б). МАТЬ <—————— ЛЮБИТ <—————— ?
кого? что делать?
Тривиальность рассмотренного примера убеждает в необходимости режима возвратов при реализации неформальных процедур.
Слайд 9
Логический вывод
Важность логического вывода становится очевидной уже
при рассмотрении простейших информационно-логических процедур.
Предположим, что некоторая база
данных содержит сведения об отношениях "o — ОТЕЦ у" и "х — МАТЬ у".
Чтобы обработать запросы типа:
ИВАНОВ А.И. — ДЕД ПЕТРОВА В.А.?
ПЕТРОВ В.А. — ВНУК ИВАНОВА А.И.?
необходимо либо ввести в базу данных также и сведения об отношениях "х — ДЕД у" и "х — ВНУК у", либо объяснить системе, как из отношений ОТЕЦ, МАТЬ извлечь искомую информацию.
Слайд 10
Реализация первой возможности связана с неограниченным ростом избыточности
базы данных.
Вторая возможность при традиционном алгоритмическом подходе требует
написания все новых и новых программ для реализации новых типов запросов.
Слайд 11
Логический вывод позволяет расширять возможности "общения" наиболее просто
и наглядно. Так, для приведенных типов запросов системе достаточно
будет сообщить три правила:
х—ДЕД у если х—ОТЕЦ а и а—РОДИТЕЛЬ у
2. х—РОДИТЕЛЬ у если х—ОТЕЦ у или х—МАТЬ у
3. х—ВНУК у если у—ДЕД х
Эти правила содержат естественные и очевидные определения понятий ДЕД, РОДИТЕЛЬ, ВНУК.
Поясним в чем состоит логический вывод для запроса "А—ДЕД В?" в предположении, что в базе данных имеются факты: А—ОТЕЦ Б и Б—МАТЬ В. При этом для упрощения опустим тонкости, связанные с падежными окончаниями.
Пользуясь определением 1 система придет к необходимости проверки существования такого индивидуума а, что факты А—ОТЕЦ а и а—РОДИТЕЛЬ В истинны. Если такой а существует, то А—ДЕД В, если не существует такого а, то А не является дедом В.
Слайд 12
Зависимость продукций
Мы могли бы использовать в таблице
решений только конкретные факты, например правила ДОМ --> ДОМА,
МАМА --> МАМЫ и т. д., и динамичность соответствующей таблицы решений была бы восстановлена — подобные правила можно было бы вводить в произвольном порядке!
Однако цена подобной "динамичности" окажется непомерно высокой — полный отказ от обобщенных правил.
Слайд 13
Продукционные системы с исключениями
Если отношение "правило—исключение" встроено
в систему, она сама может понять, что преобразование ПАЛКА
--> ПАЛКЫ незаконно.
При этом система должна руководствоваться простым принципом:
если применимо исключение, общее правило запрещено.
Соответствующие системы будем называть системами с исключениями.
Отношение "общее правило — исключение" безусловно полезно для понимания системой уместности правил. Можно сказать, что это отношение устанавливает автоматически (по умолчанию) наиболее типичное для неформальных процедур взаимодействие правил:
— исключение "вытесняет" общее правило.
— при пересечении разрешены оба правила.
Слайд 14
Разумеется, возможны ситуации, когда необходимо поступать наоборот:
— исключение не запрещает общего правила
— при пересечении одно из правил запрещено.
Пусть дано, например, общее правило х --> р1 и его исключение Ах --> р2.
Таким образом, для произвольного слова необходима реакция р1.
Для слова же, начинающегося с буквы А, исполняется реакция р2 — по умолчанию для таких слов реакция р1 незаконна.
Предположим, однако, что по условию конкретной задачи для слов, начинающихся с А, реакция р1 также допустима. В этом случае введение нового правила Ах --> р1 снимает запрет на реакцию р1 в ситуации Ах.
Аналогичный способ годится для пересечения правил.