Презентация на тему Методы и средства хранения информации

часов
Самостоятельная работа студента – 90 часов
Виды контроля:
Модульный контроль (тестирование)
Защита

лабораторных работ
ЗАЧЕТ

ОРГАНИЗАЦИИ ХРАНЕНИЯ ДАННЫХ В СУБД
РОЛЬ И ЗАДАЧИ ЗУ В

СОВРЕМЕННЫХ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМАХ И ЭВМ
КЛАССИФИКАЦИЯ УСТРОЙСТВ ХРАНЕНИЯ ИНФОРМАЦИИ
ОСНОВНЫЕ ПАРАМЕТРЫ ВЗУ
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ НОСИТЕЛЕЙ ИНФОРМАЦИИ
МАГНИТНЫЕ НАКОПИТЕЛИ
ОПТИЧЕСКИЕ НАКОПИТЕЛИ(НАКОПИТЕЛИ НА КОМПАКТ-ДИСКАХ, DVD)
ОТКАЗОУСТОЙЧИВЫЕ СИСТЕМЫ ХРАНЕНИЯ ДАННЫХ. RAID-МАССИВЫ
УСТРОЙСТВА ДЛЯ РЕЗЕРВНОГО КОПИРОВАНИЯ ДАННЫХ

первый элемент(голову) списка.
ЛИНЕЙНЫЕ И НЕЛИНЕЙНЫЕ СТРУКТУРЫ ДАННЫХ. ЛИНЕЙНЫЕ

СПИСКИ И БИНАРНЫЕ ДЕРЕВЬЯ ПОИСКА.

Список – это линейная динамическая структура данных. Каждый элемент такой структуры, в простейшем случае содержит два поля:
поле данных;
поле – указатель на следующий элемент.

С помощью указателя каждый из элементов списка связывается со следующим элементом (в случае однонаправленного списка)

Голова

БИНАРНЫЕ ДЕРЕВЬЯ ПОИСКА.
Основным отличием списка от массива является

то, что список является динамической структурой. Это позволяет:
создавать список, не резервируя лишнего места в памяти
создавать список той длины, которая необходима программе на данный момент времени, не опасаясь его переполнения.

Однако, в списке отсутствует возможность сразу обратиться к произвольному элементу, что существенно замедляет поиск (в массиве доступ к любому элементу может быть получен с использованием индекса).
Добавление элементов, как правило, осуществляется в конец списка, поэтому желательно также всегда хранить указатель и на последний элемент – хвост списка.

Голова

Хвост

БИНАРНЫЕ ДЕРЕВЬЯ ПОИСКА.
При удалении некоторого элемента списка необходимо

найти предыдущий и следующий элементы и связать их (указатель предыдущего должен теперь указывать на следующий, а не на удаляемый). Только после этого можно освободить память от удаляемого элемента.

Голова

БИНАРНЫЕ ДЕРЕВЬЯ ПОИСКА.
В отличии от линейного списка, дерево

– нелинейная динамическая структура данных.

Древовидная структура характеризуется:
множеством узлов (nodes), происходящих от единственного начального узла, называемого корнем (root).
Каждый узел может быть родителем (parent), указывающим на 1 или более узлов, называемых сыновьями (children).
Каждый некорневой узел имеет только одного родителя, и каждый родитель имеет 0 или более сыновей.
Узел, не имеющий детей, называется листом (leaf).

Рисунок 1 – Древовидная структура

БИНАРНЫЕ ДЕРЕВЬЯ ПОИСКА.
Длина пути от корня к какому-либо

узлу есть уровень узла. Уровень корня равен 0. Каждый сын корня является узлом 1-го уровня, следующее поколение – узлами 2-го уровня и т.д. Например, на рисунке 2 узел F является узлом 2-го уровня (с длиной пути 2).
Глубина (depth) дерева есть его максимальный уровень. Понятие глубины также может быть описано в терминах пути. Глубина дерева есть длина самого длинного пути от корня до узла. На рисунке 2 глубина дерева равна 3.

Рисунок 2 - Уровень узла и длина пути

БИНАРНЫЕ ДЕРЕВЬЯ ПОИСКА.
Cосредоточимся на ограниченном классе деревьев, где

каждый родитель имеет не более двух сыновей.
Такие деревья называются бинарными деревьями. Бинарные деревья (binary trees) имеют унифицированную структуру, допускающую разнообразные алгоритмы прохождения и эффективный доступ к элементам.

Рисунок 3 - Бинарные деревья

На уровне n бинарное дерево может содержать от 1 до 2n узлов. Число узлов, приходящееся на уровень, является показателем плотности дерева. На рисунке 3 дерево А содержит 8 узлов при глубине 3, в то время как дерево B содержит 5 узлов при глубине 4. Последний случай является особой формой, называемой вырожденным (degenerate) деревом, у которого есть единственный лист (E) и каждый нелистовой узел имеет только одного сына.

БИНАРНЫЕ ДЕРЕВЬЯ ПОИСКА.
Законченные бинарные деревья (complete binary tree)

- деревья глубины N, где каждый уровень 0...N-1 имеет полный набор узлов, и все листья уровня N расположены слева.
Законченное бинарное дерево, содержащее 2N узлов на уровне N, является полным.
На рисунке показаны законченное и полное бинарные деревья:

БИНАРНЫЕ ДЕРЕВЬЯ ПОИСКА.
Законченные и полные бинарные деревья обладают

следующими свойствами:
На нулевом уровне имеется 20 узлов, на первом - 21, на втором - 22 и т.д. На первых k-1 уровнях имеется 2k-1 узлов: 1 + 2 + 4 + ... + 2k­1 = 2k-1
На уровне k количество дополнительных узлов колеблется от 1 до 2k (полное). В полном дереве число узлов равно:1 + 2 + 4 + ... + 2k-1 + 2k = 2k+1 - 1
Число узлов законченного бинарного дерева удовлетворяет неравенству:2k < N < 2k-1 - 1 < 2k-1; решая его относительно k, имеем: k < log2 (N) < k+1

В случае, если бинарное дерево упорядочено, т.е. для каждого поддерева выполняется условие – значение каждого узла левого поддерева меньше значения корневого узла, а значение любого узла правого поддерева больше или равно значения корневого узла – такое дерево называется бинарным деревом поиска.
Упорядоченность дерева накладывает свои особенности на процедуры создания дерева, добавления и удаления элементов (узлов), а также поиска.

БИНАРНЫЕ ДЕРЕВЬЯ ПОИСКА.
Очевидно, что бинарное дерево поиска будет

иметь существенные преимущества перед линейным списком по времени поиска данных.
Действительно, если для поиска в линейном списке, содержащем N элементов, в худшем случае нужно выполнить N операций сравнения, то в случае полного бинарного дерева поиска, содержащего такое же количество элементов, наибольшее количество сравнений - log2(N).
Очевидно, что чем больше N, тем более выгодно использование при поиске бинарного дерева поиска по сравнению с линейным списком.

Однако, при сравнении двух рассматриваемых структур по времени выполнения операций добавления элементов следует отметить преимущество линейного списка.
Действительно, при добавлении в бинарное дерево поиска сначала придется найти подходящий лист(выполнив при этом в случае полного дерева log2(N) операций сравнения), тогда как добавление к списку, в случае хранения хвоста происходит сразу же.

БИНАРНЫЕ ДЕРЕВЬЯ ПОИСКА.
Как известно, при удалении узла из

бинарного дерева поиска, необходимо сначала найти требуемый элемент, а затем может возникнуть необходимость модификации дерева (замещения удаляемого узла), при этом требуется время и на поиск замещающего узла.
В списке же, удаление узла также сводится к его поиску (причем, в однонаправленном списке желательно сразу же найти и предыдущий элемент), после чего переопределением указателя предыдущего элемента текущий элемент может быть удален из списка.
Таким образом, в случае небольшого числа элементов, возможно и преимущество линейного списка, однако, с ростом числа элементов все существеннее будет преимущество бинарного дерева поиска.

обстоятельств бинарное дерево поиска может оказаться вырожденным. Тогда высота

его будет N, и доступ к данным существенно замедлится.
Существует модифицированный класс бинарных деревьев, обладающих всеми преимуществами бинарных деревьев поиска и никогда не вырождающихся.
Они называются сбалансированными или AVL-деревьями (по именам авторов Адельсона-Вельского и Ландиса)

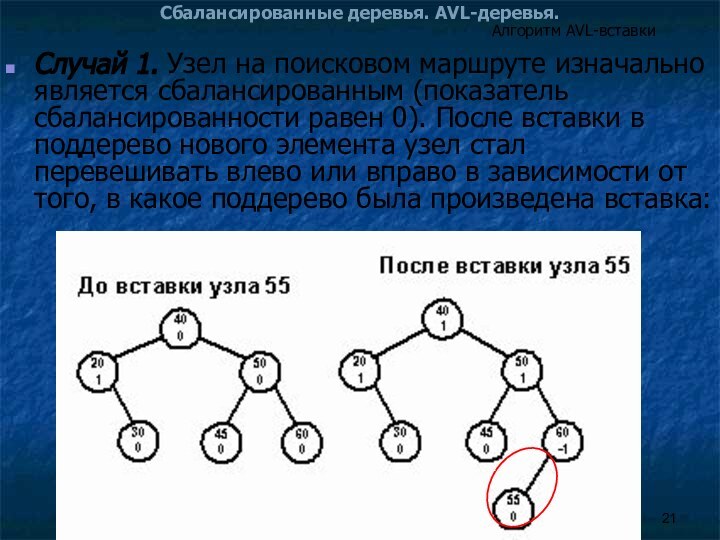
Под сбалансированностью понимают то, что для каждого узла дерева высоты обоих его поддеревьев различаются не более чем на 1.

Строго говоря, этот критерий нужно называть AVL-сбалансированностью в отличие от идеальной сбалансированности, когда для каждого узла дерева количества узлов в левом и правом поддеревьях различаются не более чем на 1.

дерева не превышает log2N.
Таким образом, AVL-дерево является структурой

хранения, обеспечивающей быстрый доступ к данным, независимо от порядка поступления ключей при его построении.

Очевидно, что AVL-деревья имеют структуру, аналогичную бинарным деревьям поиска.
Все операции идентичны описанным для бинарных деревьев, за исключением операций добавления и удаления узлов.

В случае AVL-деревьев, после выполнения каждой из этих операций проверяется соотношение высот левого и правого поддеревьев тех узлов, которые затронула операция(от добавленного/удаленного узла до корня).

Значение, содержащее разность высот правого и левого поддеревьев - показатель сбалансированности - хранится в дополнительном поле каждого узла AVL-дерева.

узел «перевешивает влево», так как высота левого поддерева больше,

чем высота правого поддерева.
При положительном показателе сбалансированности узел «перевешивает вправо».
Сбалансированный по высоте узел имеет показатель сбалансированности равный 0.
В AVL-дереве показатель сбалансированности каждого узла должен принимать значения из диапазона [-1, 1].

AVL-деревья со значениями показателя сбалансированности

нового узла в AVL-дерево такой же, как и в

случае бинарного дерева поиска.
Осуществляется спуск по левым и правым сыновьям, пока не встретится пустое поддерево, а затем производится предварительная вставка нового узла в этом месте(возможно использование рекурсивного спуска).
Обновление показателей сбалансированности узлов, затронутых при добавлении ведется в обратном порядке(при возвращении из рекурсии). При этом показатель сбалансированности родительского узла можно скорректировать после изучения эффекта от добавления нового элемента в одно из его поддеревьев. Необходимость корректировки определяется для каждого узла, входящего в поисковый маршрут.
Есть три возможных ситуации. В двух первых случаях узел сохраняет сбалансированность, и реорганизация поддеревьев не требуется. Нужно лишь скорректировать показатель сбалансированности данного узла. В третьем случае разбалансировка дерева требует модификации дерева – выполнения процедур одинарного или двойного поворотов узлов.

Алгоритм AVL-вставки

двух первых случаях узел сохраняет сбалансированность, и реорганизация поддеревьев

не требуется. Нужно лишь скорректировать показатель сбалансированности данного узла.

В третьем случае разбалансировка дерева требует модификации дерева – выполнения процедур одинарного или двойного поворотов узлов.

Алгоритм AVL-вставки

маршруте изначально является сбалансированным (показатель сбалансированности равен 0). После

вставки в поддерево нового элемента узел стал перевешивать влево или вправо в зависимости от того, в какое поддерево была произведена вставка:

Алгоритм AVL-вставки

узла перевешивает, и новый узел вставляется в более легкое

поддерево. Узел становится сбалансированным:

Алгоритм AVL-вставки

узла перевешивает, и новый узел помещается в более тяжелое

поддерево. Очевидно, что при этом нарушается условие сбалансированности дерева, так как показатель сбалансированности выходит за пределы -1..1.
Чтобы восстановить равновесие, нужно выполнить модификацию дерева – одну из процедур поворота дерева.

Алгоритм AVL-вставки

Повороты AVL-дерева

Повороты необходимы, когда родительский узел (обозначим его P) становится разбалансированным - баланс фактор становится равен 2 или -2.
Одинарный поворот вправо (single right rotation) происходит тогда, когда родительский узел P и его левый сын (обозначим его LC) начинают перевешивать влево после вставки узла в позицию X.

своего родителя, который становится правым сыном.
Бывшее правое поддерево узла

LC (ST) присоединяется к P в качестве левого поддерева.

Алгоритм AVL-вставки. Одинарный поворот.

Одинарный поворот уравновешивает как родителя, так и его левого сына.

void AVLTree::SingleRotateRight (AVLTreeNode* &p)
{
AVLTreeNode *lc;
// установить lc

на левое поддерево
lc = p->Left();
// скорректировать показатели сбалансированности
p->balanceFactor = balanced;
lc->balanceFactor = balanced;
p->left = lc->Right();
// переместить p в правое
//поддерево узла lc.
lc->right = p;
// сделать lc новым
//корнем.
p = lc;
}

rotation) нужен тогда, когда родительский узел (P) становится перевешивающим

влево, а его левый сын (LC) перевешивающим вправо.
NP – корень правого перевешивающего поддерева узла LC. Тогда в результате поворота:

Алгоритм AVL-вставки. Двойной поворот.

1. Узел NP замещает родительский узел.

2. Бывший родитель P становится правым сыном NP .

3. Осиротевшие поддеревья NP распределяются к LC и P .

дополнительных затрат на поддержание сбалансированности при вставке или удалении

узлов(повороты требуются примерно в половине случаев вставок и удалений).

Если в дереве постоянно происходят вставки и удаления элементов, эти операции могут значительно снизить быстродействие.

С другой стороны, если данные превращают бинарное дерево поиска в вырожденное, то теряется поисковая эффективность.

Таким образом, применение AVL-деревьев целесообразно в тех случаях, когда поиск является доминирующей операцией.
В таких случаях сначала происходит построение дерева, а потом производится поиск по этому дереву с небольшим количеством изменений.

сих пор задача поиска решалась в предположении, что данные

хранятся во внутренней(оперативной) памяти

Если структуры данных, например, бинарное дерево поиска или AVL-дерево, расположены не в оперативной памяти, а на диске, то они становятся малоэффективными.

При работе с данными, хранящимися на внешних носителях, целесообразно сокращать количество обращений к носителю.

Если предположить, что в одном узле дерева, хранящегося на диске, будет расположен не один, а несколько элементов – узел в этом случае называется страницей дерева и за одно обращение к диску будет считываться целая страница, то число обращений к диску при поиске существенно уменьшится.

Например, при N=1млн., число обращений к обычному дереву равно примерно 20(log2106≈20), а при постраничном чтении, например, по 7 элементов, число обращений сократится в 3 раза, что ускорит поиск в 3 раза.

1970 году Р. Байер и Маккрейт предложили структуру данных,

названную B-деревьями, позволяющую производить поиск по большому дереву, расположенному во внешней памяти.

Определение: Б-деревом порядка n называется динамическая структура обладающая следующими свойствами:

Каждая страница имеет не более 2n элементов
Каждая страница, кроме корневой, имеет не менее n элементов. Корневая страница может иметь от 1 до 2n элементов
Каждая страница является либо листовой, либо содержит m+1 потомков, где m - число элементов на этой странице
Все листья находятся на одном уровне

страница имеет не более 2n элементов
Каждая страница, кроме

корневой, имеет не менее n элементов. Корневая страница может иметь от 1 до 2n элементов
Каждая страница является либо листовой, либо содержит m+1 потомков, где m - число элементов на этой странице
Все листья находятся на одном уровне

на страницах B-деревьев располагаются в возрастающем порядке. Если спроецировать

Б-дерево на один-единственный уровень, включая потомков между ключами их родительской страницы, то ключи идут в возрастающем порядке слева направо.

Память в B-дереве всегда используется минимум на 50%, так как страницы всегда заполнены как минимум наполовину!

задан некоторый аргумент поиска х и страница имеет вид:
Алгоритм

поиска элемента в B-дереве

Если страница уже считана в оперативную память и можно воспользоваться обычными методами поиска среди ключей ki ... km.
Если m достаточно большое, то это может быть двоичный поиск, если же оно мало, то можно воспользоваться простым последовательным перебором.

Если поиск элемента х на странице неудачен, то мы попадаем в одну из следующих ситуаций:

ki < х < ki+1 для 1 ≤ i < m. Поиск продолжается на странице pi.
km < х. Поиск продолжается на странице рm.
х < k1. Поиск продолжается на странице р0.

в B-дерево проводится только в листовые страницы. При этом

поиск листовой страницы для вставки элемента происходит согласно алгоритма поиска в B-дереве.

Включение элемента в B-дерево

Если новый элемент нужно поместить на страницу с m < 2n элементами, то процесс включения элемента затрагивает лишь одну страницу B-дерева.

Включение в заполненную страницу затрагивает структуру дерева и может привести к появлению новых страниц.

элемента в B-дерево
1. Обнаруживается, что ключ 23 отсутствует. Включение

в страницу A невозможно, поскольку она уже заполнена.
2. Страница A разделяется на две страницы (вводится новая страница C).
3. Ключи — их всего 2n+1—поровну распределяются в С и A, а серединный ключ переносится на один уровень вверх на «родительскую» страницу.

элемента в B-дерево
Процесс добавления элементов в Б-дерево представлен на

рисунке, причем включаемые ключи идут в таком порядке:
20; 40 10 30 15; 35 7 26 18 22; 5; 42 13 46 27 8 32 38 24 45 25;

исключении элемента из B-дерева можно выделить два случая:
1. Исключаемый

элемент находится на листовой странице.
2. Элемент находится не на листовой странице.

Исключение элемента из B-дерева

В первом случае, удаление элемента с листовой страницы не вызовет затруднений, если эта страница содержит более n элементов.

Если же количество элементов на странице после удаления станет меньше n, то необходимо проделать некоторые действия, чтобы предотвратить нарушение второго условия B-дерева (m>=n).

В этом случае для текущей страницы необходимо позаимствовать элемент с одной из соседних страниц. Если соседняя страница содержит более n элементов, то происходит перемещение крайнего элемента (ближнего к текущей странице) в родительскую страницу, а элемент из родительской страницы в текущую.

том случае, если занять элемент на соседних страницах невозможно

(они содержат по n элементов), выполняется процедура слияния двух страниц.

Исключение элемента из B-дерева

Так как общее число элементов на двух соседних страницах после удаления становится равным 2n-1, то, забирая элемент с родительской страницы, получим одну страницу содержащую 2n элементов. При этом вторая освободившаяся страница уничтожается. Процесс слияния страниц в точности обратен процессу разделения страницы.

элемента из B-дерева
Рассмотрим деградацию Б-дерева в случае удаления ключей

в последовательности:
25 45 24; 38 32; 8 27 46 13 42; 5 22 18 26; 7 35 15;

элементов на странице
#define ITEM_ON_LEVEL 2*LEVEL
//задаем максимальное количество страниц
#define MAX_PAGES

2000
//описываем структуру хранящую информацию о
//занятости страниц в файле
struct file_info{
//отводим по 1 байту для описания состояния страниц
//пока 1 -занята 0 - свободна
unsigned char m_state[MAX_PAGES];
//храния смещение относительно начала файла для корневой страницы
int m_irootoffset;
//смещение начала записи этой структуры в файл
int offset;
};

//массив элементов на странице
DATA m_arkeys[ITEM_ON_LEVEL];
//массив смещений на

доцерние страницы
int m_arpages[ITEM_ON_LEVEL+1];
//текущее кол-во элементов на странице
int m_ikeys;
//конструктор по умолчанию
CBTreePage();
//метод записи страницы в файл
bool SavePage(fstream &file,int offset);
//метод загрузки страницы из файл
bool LoadPage(fstream &file,int offset);
friend class CBTree;
};

страницы
int m_iroot;
//максимальное смещение занимаемое страницами дерева
int max_offset;
//структура описывающая файл

текущего дерева
file_info m_finfo;
// колличество страниц
int NumberOfPages;
//используются public методом AddItem
bool Add(int &root,DATA &item, int &up_page, DATA &up_item,bool &split);
void SplitPage(CBTreePage &page, int spot, DATA &up_item, int &up_page);
//используются public методом DeleteItem
bool DeleteFromPage(int page,DATA &item,bool &too_small);
void SwapItem(CBTreePage &root,int key_pos, int child, bool&too_small);
void TooSmall(CBTreePage &parent, int child, int child_num, bool &too_small);
//методы для записи и считывания информации о дереве в(из) файл(файла)
void SaveFileInfo();
void LoadFileInfo();
public:
//конструктор по умолчанию
CBTree();
//иниализатор, вызывается в конструкторе формы
void Inializator();
//подготовка файла, вызывается в конструкторе формы
void Prepare();
// метод, позволяющий определить колличество страниц
int CountPages(){return NumberOfPages;};
// метод, позволяющий определить глубину дерева
int CountDepth();
//дескриптор текущего файла
fstream m_hfile;
//метод позволяющий получить смещение свободной страницы
int GetOffset();
//метод освобождающий страницу
void FreeOffset(int offset);
//метод позволяющий найти элемент по ключю и получить другую инвормацию о элементе
bool Find(DATA &item);
//метод добавления элемента
bool AddItem(DATA &item);
//метод удаления элемента
bool DeleteItem(DATA &item);
//метод позволяющий получить смещение корневой страницы
int GetRootOffSet() {return m_iroot;}
//метод очищающий дерево
void ClearTree();
//деструктор
~CBTree();
};

в таблицах баз данных можно использовать предварительное упорядочивание таблицы

в соответствии со значениями ключей.

Потери времени на повторное упорядочивание таблицы могут значительно превышать выигрыш от сокращения времени поиска. Поэтому для сокращения времени доступа к данным в таблицах часто используется так называемое случайное упорядочивание или хеширование.

При этом данные организуются в виде таблицы при помощи хеш-функции h, используемой для “вычисления” адреса по значению ключа.

Хеш-таблицы - один из наиболее эффективных способов реализации словарей (словарь - абстрактный тип данных (множеств) с операторами вставки, удаления и проверки членства INSERT, DELETE и MEMBER).

для любых двух неодинаковых ключей дает неодинаковые адреса:
Такая

организация данных носит название “совершенное хеширование“.

В случае заранее неопределенного множества значений ключей и ограниченной длины таблицы подбор совершенной функции затруднителен.

ссылку на данные. Ключ отображается во множество целых чисел

посредством хеш-функции (hash function). Полученное в результате значение затем используется для доступа к данным.

Ключи и хеш-функция

Предположим, Key – положительное целое, а HF(Key) – значение младшей цифры числа Key. Тогда диапазон индексов равен 0-9.
Например, если Key = 49, HF(Key) = HF(49) = 9.
Эта хеш-функция в качестве возвращаемого значения использует остаток от деления на 10.
// Хеш-функция, возвращающая младшую цифру ключа
int HF(int key){ return key % 10;}

возникать ситуации, когда для двух неодинаковых ключей функция вычисляет

один и тот же адрес. Данный случай носит название “коллизия”, а такие ключи называются “ключи-синонимы”.

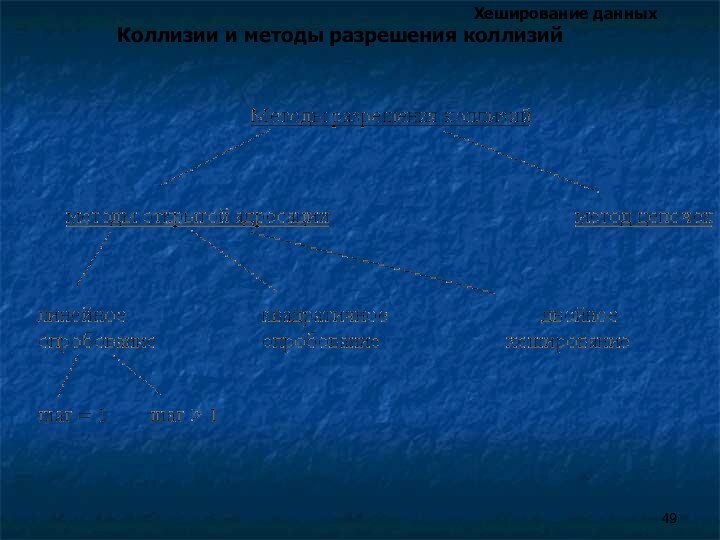
Коллизии и методы разрешения коллизий

Для разрешения коллизий используются различные методы, которые в основном сводятся к методам “цепочек“ и “открытой адресации“.

хеш-таблице с цепочками переполнения:
вычисляется адрес по значению ключа.

осуществляется последовательный поиск в списке, связанном с вычисленным адресом.

Процедура удаления из таблицы сводится к поиску элемента и его удалению из цепочки переполнения.

адресации состоят в том, чтобы, пользуясь каким-либо алгоритмом, обеспечивающим

перебор элементов таблицы, просматривать их в поисках свободного места для новой записи. Иногда данный метод хеширования называют закрытым, внутренним, или прямым хешированием.

Линейное опробование сводится к последовательному перебору элементов таблицы с некоторым фиксированным шагом a=h(key) + c*i , где i – номер попытки разрешить коллизию. При шаге равном единице происходит последовательный перебор всех элементов после текущего.

отличается от линейного тем, что шаг перебора элементов не

линейно зависит от номера попытки найти свободный элемент:
a = h(key2) + c*i + d*i2.
Благодаря нелинейности такой адресации уменьшается число проб при большом числе ключей-синонимов.

разновидность метода открытой адресации, которая называется двойным хешированием, основана

на нелинейной адресации, достигаемой за счет суммирования значений основной и дополнительной хеш-функций:
a=h1(key) + i*h2(key).

и поиска для метода линейного опробования:
Вставка:
i = 0
a

= h(key) + i*c
Если t(a) = свободно, то t(a) = key, записать элемент, стоп элемент добавлен
i = i + 1, перейти к шагу 2

Поиск:
i = 0
a = h(key) + i*c
Если t(a) = key, то стоп элемент найден
Если t(a) = свободно, то стоп элемент не найден
i = i + 1, перейти к шагу 2

удаления дело обстоит не так просто, так как она

в данном случае не будет являться обратной процедуре вставки.

В том случае, если за удаляемым элементом в результате разрешения коллизий были размещены элементы с другими ключами, то поиск этих элементов после удаления всегда будет давать отрицательный результат, так как алгоритм поиска останавливается на первом элементе, находящемся в состоянии свободно.

Скорректировать эту ситуацию можно различными способами. Наилучший из них состоит в том, что для элементов хеш-таблицы добавляется состояние “удалено”. Данное состояние в процессе поиска интерпретируется, как занято, а в процессе добавления - как свободно.

вставки, поиска и удаления для хеш-таблицы, имеющей три состояния

элементов.
Вставка:
i = 0
a = h(key) + i*c
Если t(a) = свободно или t(a) = удалено, то t(a) = key, записать элемент, стоп элемент добавлен
i = i + 1, перейти к шагу 2
Удаление:
i = 0
a = h(key) + i*c
Если t(a) = key, то t(a) = удалено, стоп элемент удален
Если t(a) = свободно, то стоп элемент не найден
i = i + 1, перейти к шагу 2
Поиск:
i = 0
a = h(key) + i*c
Если t(a) = key, то стоп элемент найден
Если t(a) = свободно, то стоп элемент не найден
i = i + 1, перейти к шагу 2