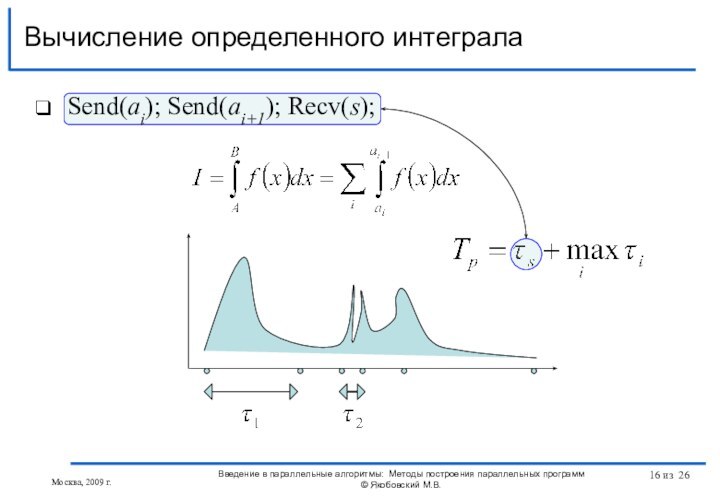
реально работающие системы, то требуется убедиться, (и убедить всех
сомневающихся) в корректности наших построений… системе часто придется работать в невоспроизводимых обстоятельствах, и мы едва ли можем ожидать сколько-нибудь серьезной помощи от тестов
Dijkstra E.W.
1966
Предварительные замечания
Москва, 2009 г.
Введение в параллельные алгоритмы: Методы построения параллельных программ © Якобовский М.В.
из 26