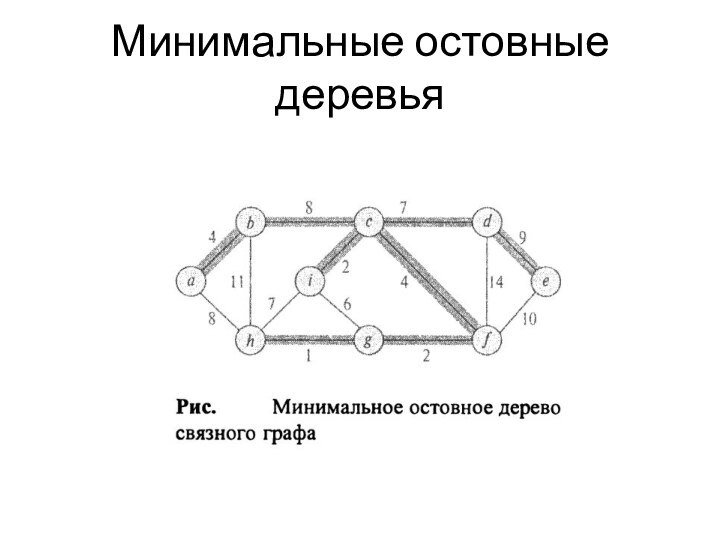
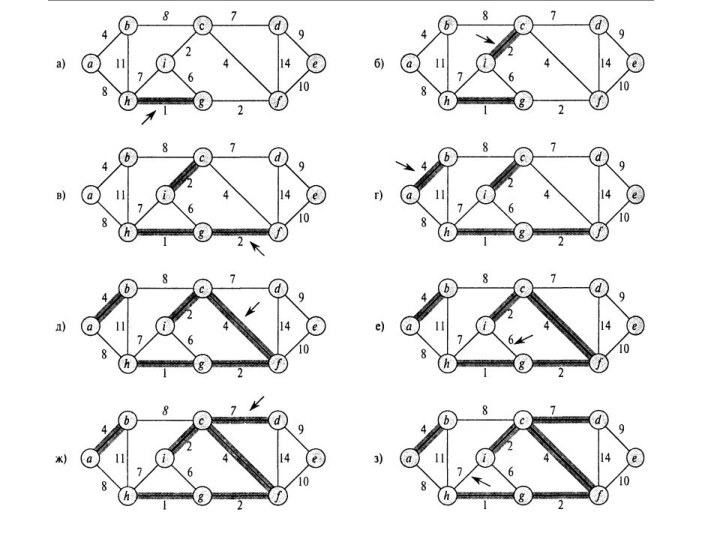
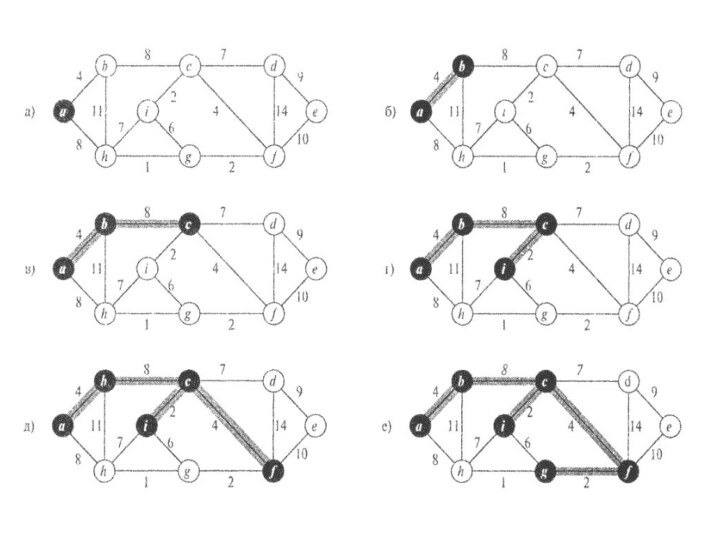
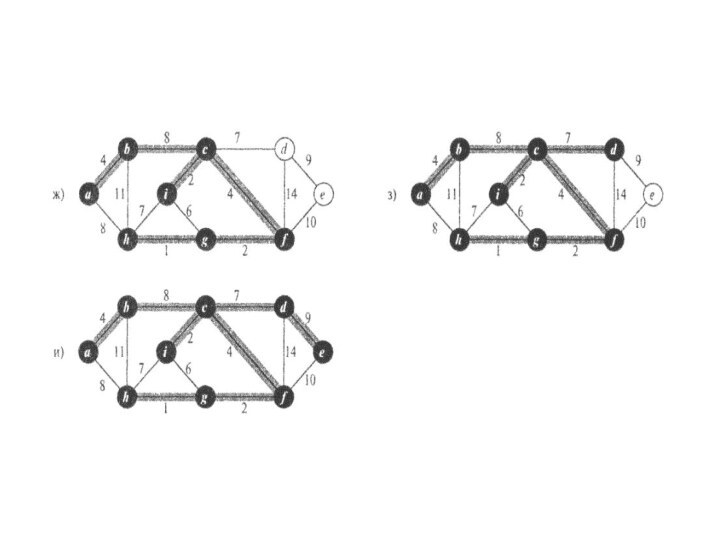
необходимо получит такую компоновку из n-1 проводов, которая использует
минимальное количество провода.Дан некий связный неориентированный граф G=(V,E), где V- множество контактов, Е- множество возможных соединений между парами контактов, и для каждого ребра (u,v)ЭЕ задан вес w(u,v), определяющий стоимость ( количество необходимого провода)соединения u и v.