Слайд 2
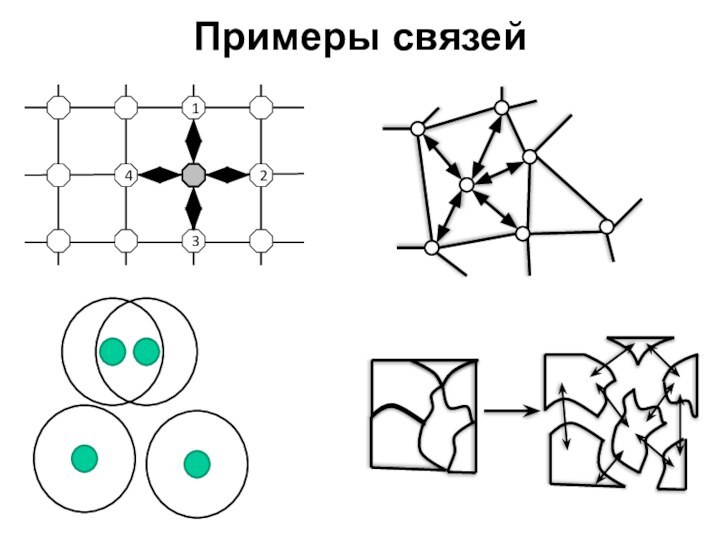
Метод решения
Стандартизация интерфейсов для объектов, из которых собирается
модель, и их связей.
Суть предлагаемого решения – локальность всех
описаний: связей, времени и алгоритмов эволюции подобластей.
Модель всей области получаем практически автоматически путем композиции подобластей. Буквальный цифровой аналог натурного моделирования.
Слайд 3
Текущее состояние разработки
В настоящий момент отлаживается третья версия
системы OST (Objects –Space – Time) на К100 (ИПМ
РАН).
Первая версия - 2009 год, кластер из нескольких РС, тесты,
решение одной двумерной задачи газовой динамики (M2DGD)
и одномерной задачи теплопроводности.
Вторая версия – 2010 год, RSC4 (ИПМ РАН) – варианты
двумерной задачи газовой динамики, тестовые задачи.
Кто работает:
Два сотрудника ИПМ РАН и кафедры «Вычислительная механика» МГУ.
Аспиранты и студенты МГУ и ИПМ РАН.
Слайд 5
Главная проблема: Джон Хэннеси, президент Стэнфордского университета –
“… когда мы начинаем говорить о параллелизме и легкости
использования действительно параллельных компьютеров, мы говорим о проблеме, которая труднее любой проблемы, с которой встречалась наука о компьютерах … Я бы запаниковал, если бы я работал в промышленности.”
Главная цель – свести трудоемкость создания параллельных моделей к трудоемкости создания последовательных моделей для максимально широкого класса задач.
Слайд 6
Миф о последовательном характере большинства решаемых задач
Уровни представления
физической области:
Физическая модель -> Математическая модель ->
Вычислительная модель
-> Программная модель -> МВС
Подобие уровней представления:
Сквозное употребление терминов. Объект, связь, интерфейс, …
Подобие проблем на разных уровнях
Параллельная эволюция частей и их взаимодействие
В общем случае невозможно восстановить из последовательной программы (алгоритма) исходный естественный параллелизм физической области.
Буквальное отображение параллельной физической модели на параллельные вычислительную и программную модель. Сохраняется деление на части и структура связей.
Слайд 7
Вычислительная модель - множество вычислительных объектов (каждый объект
- набор матриц, векторов, скаляров плюс последовательный алгоритм –
это представление физической подобласти) отображается на множество программных объектов, распределенных по МВС (RPC) – программная модель.
Слайд 8
3. Способы композиции на уровне вычислительной модели.
3.1. Метод Шварца для декомпозиции
областей.
3.2. Метод композиции вычислительных объектов – построение области путем композиции первичных подобластей с выделением приграничных полос между подобластями.
3.3. Использование приграничных «потоков» для композиции подобластей.
и т.д.
Конкретных способов много. Стандарты для достаточно широкого класса случаев отсутствуют.
Слайд 9
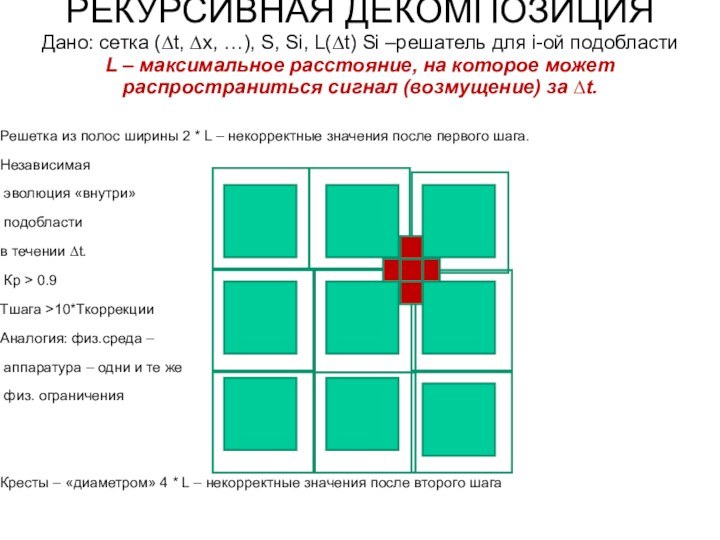
РЕКУРСИВНАЯ ДЕКОМПОЗИЦИЯ
Дано: сетка (∆t, ∆x, …), S, Si,
L(∆t) Si –решатель для i-ой подобласти
L – максимальное расстояние,
на которое может распространиться сигнал (возмущение) за ∆t.
Решетка из полос ширины 2 * L – некорректные значения после первого шага.
Независимая
эволюция «внутри»
подобласти
в течении ∆t.
Кр > 0.9
Тшага >10*Ткоррекции
Аналогия: физ.среда –
аппаратура – одни и те же
физ. ограничения
Кресты – «диаметром» 4 * L – некорректные значения после второго шага
Слайд 10
4. Композиция программных объектов в системе OST (Objects
– Space -Time).
4.1. Определение интерфейса между объектом и его
окружением.
4.1.1 Интерфейс самого объекта для объектов из его окружения (окрестности) в виде списка операций, выполняемых объектом, и их параметров.
Язык JAVA
interface Left_Neighbour {
int get_border(double left_array[]);
}
Слайд 11
4.1.2. Интерфейс окружения для объекта в виде
“списка формальных соседей” - объектов с их интерфейсами.
(Left_Neighbour Left,
Right_Neighbour Right)
Здесь:
Left_Neighbour – указание на интерфейс с соседом;
Left – имя ссылки на соседа, в которую OST после определения связей подставит ссылку на фактического соседа.
Вызов операции в соседе разрешен всегда, но фактически будет выполнен только при совпадении локальных времен соседей.
Слайд 12
Пример прикладного класса
Язык Python
class objectExampe(OST_Object_Abstract):
double
left_array[];
def run():
#вызов метода в соседе
self.Left_Neighbors. get_border(double left_array[]);
<…>
self.time += 1
#изменение координат
if <…>:
self.x += 1
self.setXYZT()
Слайд 13
Топология связей между объектами.
Определение связей между
объектами через локальное описание окрестности для каждого объекта. Автоматическая
замена формальных соседей на фактические во время счета.
Слайд 15
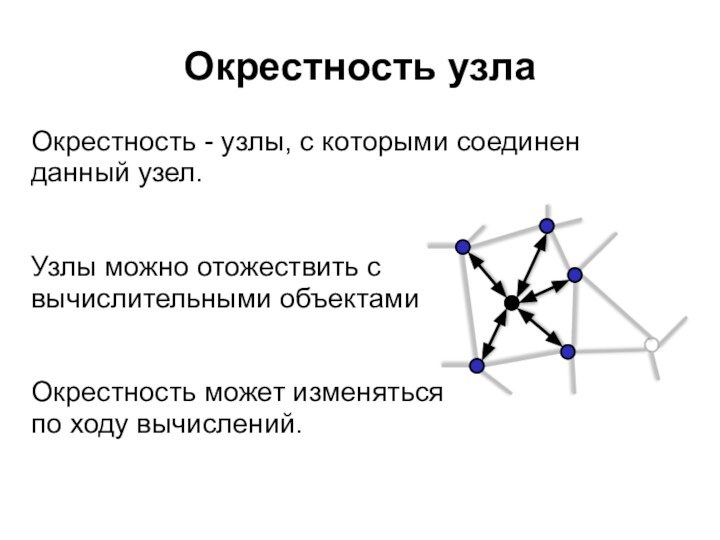
Окрестность узла
Окрестность - узлы, с которыми соединен
данный узел.
Узлы
можно отожествить с
вычислительными объектами
Окрестность может изменяться
по ходу вычислений.
Слайд 16
Локальная топология
Локальная топология – это топология, описывающая множество
соседей
для данного вычислительного объекта
в локальных координатах
Локальные координаты – система
координат, связанная с окрестностью данного объекта.
Слайд 17
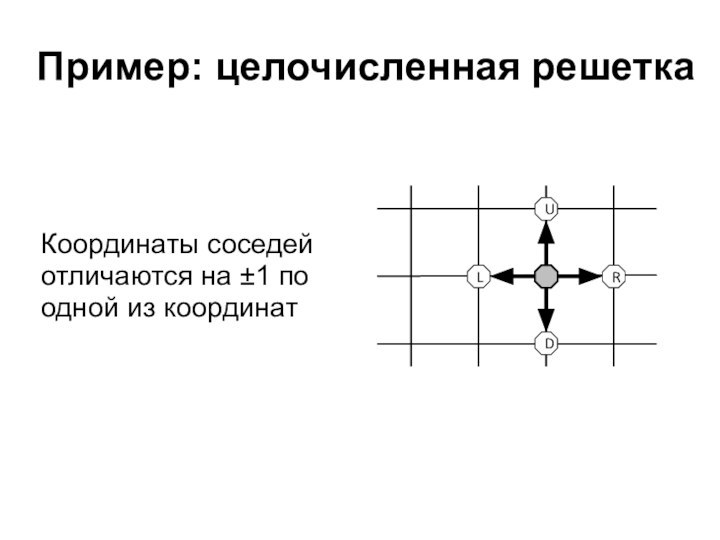
Пример: целочисленная решетка
Координаты соседей отличаются на ±1 по
одной из координат
Слайд 18
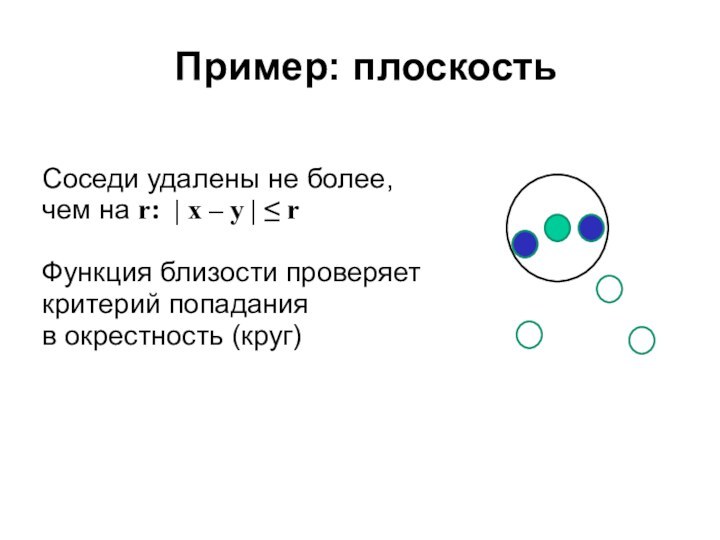
Пример: плоскость
Соседи удалены не более, чем на r:
| x – y | ≤ r
Функция близости проверяет
критерий попадания
в окрестность (круг)
Слайд 19
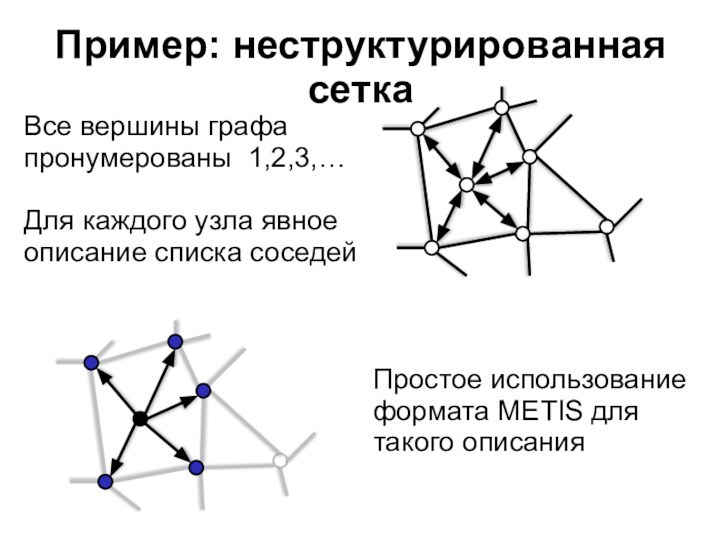
Пример: неструктурированная сетка
Все вершины графа пронумерованы 1,2,3,…
Для каждого
узла явное описание списка соседей
Простое использование формата METIS для
такого описания
Слайд 20
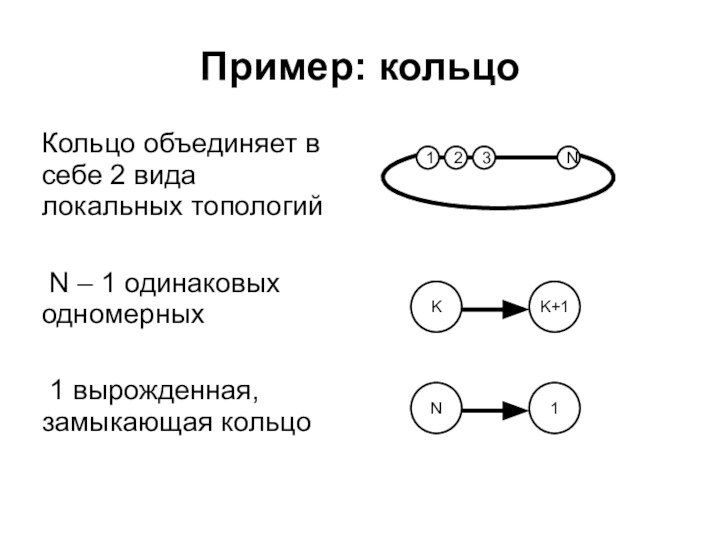
Пример: кольцо
Кольцо объединяет в себе 2 вида локальных
топологий
N – 1 одинаковых одномерных
1 вырожденная, замыкающая
кольцо
Слайд 21
Базовая топология – связный граф
Случай неструктурированной сетки
#Создание объектов
в функции инициирования модели
for :
муobject = objInit.createObject(objectClass)
данными объекта myobject >
object.array1 = <...> …
<Передача базового объекта topology в object> myobject.topology = topologyLocal()
<Занесение номера объекта в глобальный каталог>
objInit.topology.set(myobject, index)
# Задание окрестности для каждого объекта
for <…>:
<Определение списка соседей>
myobject.topology.set(
index, [nei_index1,…,nei_indexN] )
Слайд 22
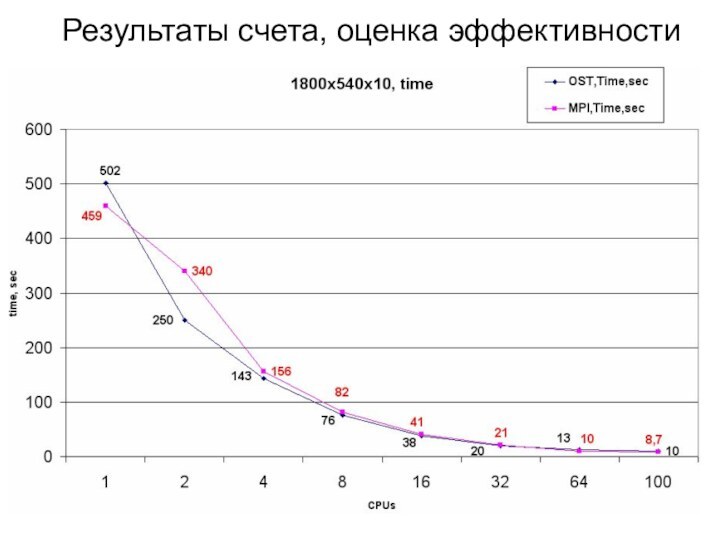
Результаты счета, оценка эффективности
Слайд 23
Что конструктивно новое
Формализация «окружения» объекта в виде списка
формальных соседей.
Автоматическое построение связей между объектами и замена
формальных соседей фактическими.
Актуализация ссылок на фактических соседей при совпадении локальных времен.
Слайд 24
Технические характеристики
1. Коэффициент эффективности параллельного счета Кр >
0.9
2. Практически автоматическая сборка (установление связей, синхронизация взаимодействия по
локальным временам объектов) автономно запрограммированных объектов (моделей физических подобластей). То-есть, трудоемкость параллельного программирования сводится к трудоемкости раздельного программированию последовательных алгоритмов для подобластей.
3. Счетная часть объектов – С++, Фортран, управляющая часть Python.
4. Средства отладки – визуализация, отладчик, профилирование и т.д.
Слайд 25
5. Хранения множества объектов программной модели в файле
объектов (базе данных). Контрольные точки и рестарты. Мобильность хранимой
модели – возможность перенести модель на другую вычислительную установку после окончания очередного этапа счета и продолжить его на новом месте. Пример, короткий отладочный счет на РС и продолжение на МВС.
6. Планировщик ресурсов, обеспечивающий автоматическую подкачку/выталкивание программных объектов между процессорами и файлом объектов в стиле подкачки страниц в операционных системах. Счет на основе “рабочего множества” объектов.









![Объект-модель Пример прикладного классаЯзык Pythonclass objectExampe(OST_Object_Abstract): double left_array[]; def](/img/tmb/12/1141115/0a41413b6e9c8ece5b46dfc60877733b-720x.jpg)