- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Операции с матрицами в MatLab 7
Содержание
- 2. *MATLAB- это уникальная коллекция реализаций современных численных методов компьютерной математики.Вычисления, визуализация, программированиеВозможности системы МатЛаб
- 3. MATLAB - уникальная коллекция реализаций современных вычислительных
- 4. В области визуализации и графики: возможность создания
- 5. Список рекомендуемой литературы : Мартынов Н.Н. Matlab 7. Элементарное введение. -М:КУДИЦ-ОБРАЗ,2005.-416с
- 6. Список рекомендуемой литературы : Юлий Кетков, Александр Кетков,
- 7. Основной интерфейс MATLABОкно командРабочая областьИстория командТекущая папкаВыбор текущей папки
- 8. Главное менюСоздать новый файлОткрыть файл МАТЛАБСохранить рабочую
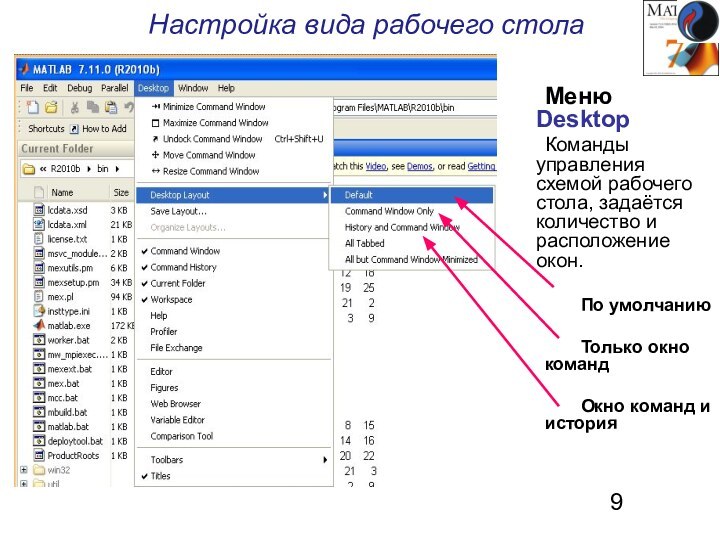
- 9. Настройка вида рабочего стола Меню Desktop Команды управления схемой
- 10. По умолчанию
- 11. В системе МАТЛАБ можно производить арифметические операции
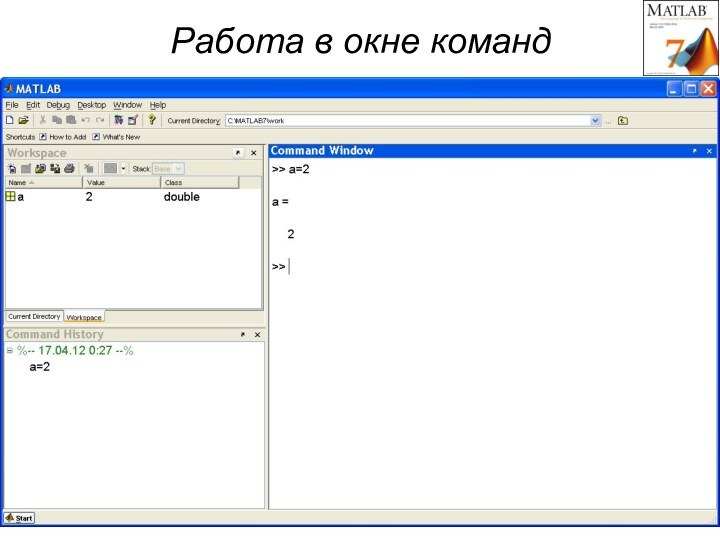
- 12. Работа в окне команд
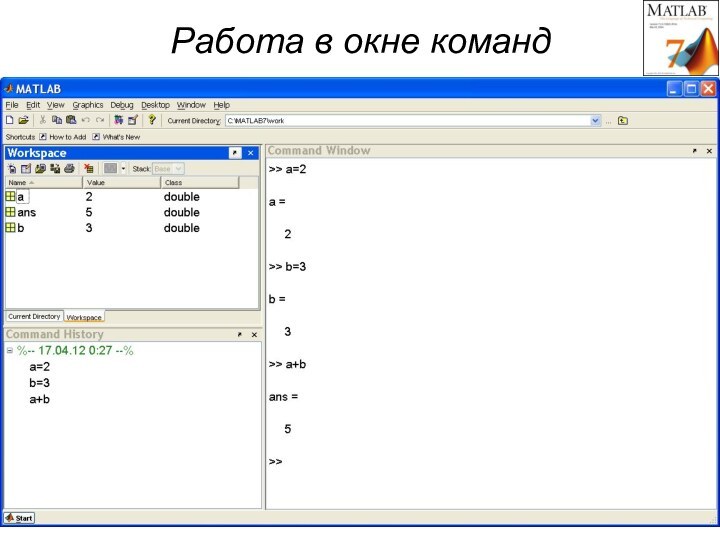
- 13. Работа в окне команд
- 14. Понятие M-файла Способы повторного ввода команд:1. Использовать
- 15. M-файл (сценарий) Содержит серию команд, которые выполняются
- 16. Команды управления окномclc – очистки окна; who
- 17. Действительные и комплексные числа-683.45677.13e13 – означает 7.13*10131.7977е+308
- 18. Форматыformat short – 4 цифры после точки
- 19. disp (‘Результаты расчета')Вывод комментария на экранВывод значения
- 20. Арифметические операторы Основные: + - *
- 21. В математических выражениях операторы имеют определенный приоритет
- 22. Элементарные алгебраические функции
- 23. Тригонометрическиe функции
- 24. Результат вычислений присваивается переменной>> x=2-3^2x =
- 25. Основной объект в системе Matlab — это
- 26. Чтобы задать вектор, достаточно перечислить его элементы,
- 27. Одномерные массивыЗадание массива:a = [ -3 4
- 28. Двумерные массивыЗадание массива:a = [ 1 2; 3 4; 5 6];Доступ к элементу:
- 29. ДиапазоныФункция magic(n) задает магическую матрицу nxn все
- 30. for i=1:3 for j=1:3
- 31. Создание массивов со случайными элементамиrand(n) и rand(m,n)
- 32. Диапазоны
- 33. Удаление строк и столбцов
- 34. Перестановка элементов
- 35. Операции над матрицамиa+b сложение скаляров, векторов или
- 36. Операции над матрицамиФункция length(V) рассчитывает количество элементов
- 37. Операции над матрицамиФункция сортировки sort(V) формирует вектор,
- 38. Операции над матрицамиabs(A) - модульdet(A)
- 39. Операции над матрицамиprod(A,1) - произведение
- 40. Операции над матрицамиsort(A) - сортировка по
- 41. Операции над матрицами[b2,INDEX]=sort(b) - возвращает отсортированный массив
- 42. Дневник работыКоманда diary открывает дневник, т.е. указывает
- 43. Решение системы линейных уравнений.В матричном виде система
- 45. Решение системы линейных уравнений>> d=det(a)d =
- 46. Решение системы линейных уравненийРешение x1=1, x2=-1, x3=2
- 47. Скачать презентацию
- 48. Похожие презентации
*MATLAB- это уникальная коллекция реализаций современных численных методов компьютерной математики.Вычисления, визуализация, программированиеВозможности системы МатЛаб























![Операции с матрицами в MatLab 7 Одномерные массивыЗадание массива:a = [ -3 4 2];a = [ -3, 4,](/img/tmb/15/1429121/f19da5cb56b15079557a202e3319c469-720x.jpg)
![Операции с матрицами в MatLab 7 Двумерные массивыЗадание массива:a = [ 1 2; 3 4; 5 6];Доступ к элементу:](/img/tmb/15/1429121/fe8ff583dd75b4068499df8a341c0ca7-720x.jpg)












![Операции с матрицами в MatLab 7 Операции над матрицами[b2,INDEX]=sort(b) - возвращает отсортированный массив и массив индексов элементов в](/img/tmb/15/1429121/3759a4d89559c65adfbdad574cfc0611-720x.jpg)





Слайд 2
*
MATLAB- это уникальная коллекция реализаций современных численных методов
компьютерной математики.
Слайд 3
MATLAB - уникальная коллекция реализаций современных вычислительных методов
матричные
и логические операторы
элементарные и специальные функции
полиномиальная арифметика
многомерные массивы, массивы
записей и ячеекдифференциальные уравнения
вычисление квадратур
поиск корней нелинейных алгебраических уравнений
оптимизация функций нескольких переменных
одномерная и многомерная интерполяция
аналитические расчёты
и многое другое
Слайд 4
В области визуализации и графики:
возможность создания двумерных
и трехмерных графиков
осуществление визуального анализа данных
В области программирования:
интерактивная среда программирования
язык программирования, близкий к обычной математической нотации
свыше 1000 встроенных математических функций
работа с текстовыми и двоичными файлами
применение программ, написанных на Си, C++, ФОРТРАН и JAVA
Средство построения графического интерфейса пользователя (GUI)
облегчает взаимодействие пользователя с системой
Возможности системы MATLAB
Слайд 5
Список рекомендуемой литературы :
Мартынов Н.Н. Matlab 7. Элементарное
введение. -М:КУДИЦ-ОБРАЗ,2005.-416с
Слайд 6
Список рекомендуемой литературы :
Юлий Кетков, Александр Кетков, Михаил
Шульц
Matlab 7. Программирование, численные методы. -БХВ-Петербург, СПб ,2005.-742
с
Слайд 7
Основной интерфейс MATLAB
Окно команд
Рабочая область
История команд
Текущая папка
Выбор текущей
папки
Слайд 8
Главное меню
Создать новый файл
Открыть файл МАТЛАБ
Сохранить рабочую область
как файл типа .mat
Предпочтения для интерфейсов МАТЛАБ (установка шрифтов,
цветов и много другого)
Слайд 9
Настройка вида рабочего стола
Меню Desktop
Команды управления схемой рабочего
стола, задаётся количество и расположение окон.
По умолчанию
Только окно команд
Окно
команд и история
Слайд 11
В системе МАТЛАБ можно
производить арифметические операции с
действительными и комплексными числами,
векторами и матрицами,
вычислять функции,
работать с полиномами и рядами,
строить графики различных функций
причём, непосредственно в интерактивном режиме, т.е. без подготовки программы
Работа в окне команд (режим калькулятора)
Слайд 14
Понятие M-файла
Способы повторного ввода команд:
1. Использовать окно
Command History
2. Применить m-файл
m-файл может содержать команды, а также
управляющиеструктуры языка MatLab.
Вызов такого файла осуществляется заданием его имени.
Имя этого файла должно иметь расширение m.
Это текстовый файл – можно создавать и редактировать
в любом текстовом редакторе (предпочтительнее – во
встроенном редакторе MatLab).
m-файлы подразделяются на 2 типа:
сценарии (script)
функции (function)
Слайд 15
M-файл (сценарий)
Содержит серию команд, которые выполняются в
режиме интерпретации построчно.
Если в команде имеется ошибка, она не
обрабатывается, и система переходит в режим ожидания.Сценарий работает только с переменными, расположенными в рабочей области MatLab.
М-функция
Отличие от сценария:
Функция может компилироваться целиком с последующим размещением исполняемого кода в памяти
Функция может иметь локальные переменные, размещаемые в собственной рабочей области
В функции могут быть входные и выходные параметры
Слайд 16
Команды управления окном
clc – очистки окна;
who –
вывод имен активных переменных;
clear – удаление всех переменных;
clear a
– удаление переменной a;File->Save Workspace as… - сохранение в
файле на диске содержимого рабочего
пространства. Расширение файла mat.
File ->Load Workspace ->указание mat-файла для загрузки
Слайд 17
Действительные и комплексные числа
-68
3.4567
7.13e13 – означает 7.13*1013
1.7977е+308 –
максимальное число realmax
2.2251e-308 – минимальное число realmin
Inf
для обозначения ∞-Inf для обозначения -∞
NaN – не число ( при делении 0/0)
2+3i
-6.789+0.834e-2*i
4-2j;
Слайд 18
Форматы
format short – 4 цифры после точки (по
умолчанию)
format long – 15 цифр после десятичной точки
format short e – короткое с плавающей точкой
format long e – длинное с плавающей точкой
format long g –выбирается наиболее удачное
format short g (с плавающей точкой или с фиксированной)
format rat – формат для вывода рациональных чисел
format bank – денежный формат (2 цифры после точки)
format loose – обычный стиль вывода в окне команд
format compact – компактный стиль вывода данных
Слайд 19
disp (‘Результаты расчета')
Вывод комментария на экран
Вывод значения а
с точностью до 3 значащих цифр
vpa(а,3)
Знак точка с запятой
в конце ввода предотвращает вывод результата на экран;
Слайд 20
Арифметические операторы
Основные: + - *
/ ^
Обратное деление \ - справа
налевоПоэлементные: .* ./ .^ .\
Операторы отношения
< > >= <= == ~=
Для комплексных чисел сравниваются только действительные части
Логические операторы
& — И | — ИЛИ ~ — НЕ
Слайд 21
В математических выражениях операторы имеют определенный приоритет исполнения.
Например, в MATLAB приоритет логических операторов выше, чем арифметических,
приоритет возведения в степень выше приоритетов умножения и деления, приоритет умножения и деления выше приоритета сложения и вычитания.
Слайд 24
Результат вычислений присваивается переменной
>> x=2-3^2
x =
-7
>>
x1=5*x
x1 =
-35
>> 1+1/2*4
ans = ans – имя переменной
по умолчанию3
Имя переменной – любая последовательность латинских букв и цифр, начинающаяся с буквы
В системе есть зарезервированные имена:
i, j, pi, имена стандартных функций и пр.
>> a=2; точка с запятой в конце строки
>> отменяет вывод результатов
Переменные
Слайд 25 Основной объект в системе Matlab — это матрицы,
или массивы. Даже скалярные величины, рассматриваются системой как матрицы
1 × 1.Вектор (одномерный массив) представляет собой строку, т. е. матрицу размера 1×n, или столбец, т. е. матрицу размера m×1.
MatLab различает строчные и прописные буквы.
Количество воспринимаемых в MatLab символов в имени переменной составляет 31.
Слайд 26 Чтобы задать вектор, достаточно перечислить его элементы, заключая
их в квадратные скобки.
Элементы векторов-строк разделяются символами «,»
(запятая) или « » (пробел).Элементы векторов-столбцов разделяются символом «;» (точка с запятой) или символом перехода на новую строку.
Слайд 27
Одномерные массивы
Задание массива:
a = [ -3 4 2];
a
= [ -3, 4, 2];
Диапазоны:
b = -3: 2 (b
= -3 -2 -1 0 1 2)b = -3:2:5 (b = -3 -1 1 3 5)
Доступ к элементу:
a(3) (будет равно 2)
Изменение элемента:
a(3) = 1
Количество элементов в массиве: length(a) (будет равно 3)
Нумерация элементов начинается с 1
Добавление элементов в массив
a(4) = 5;
a = [a 5]
Конкатенация массивов:
c = [a b]
Удаление массива (превращение в пустой массив)
a = [ ]
Слайд 29
Диапазоны
Функция magic(n) задает магическую матрицу nxn все ее
элементы не превышают n2
Можно использовать как для задания значений
векторов, так и для задания диапазонов индексации
Слайд 30
for i=1:3
for j=1:3
if j>i – 1
a(i,j)=0.893+exp(2*j);else a(i,j)=2.914-sin(j*pi/i-i);
end
end
end
Слайд 31
Создание массивов со случайными элементами
rand(n) и rand(m,n) генерируют
матрицу (nxn) или (mxn) с элементами, распределенными по равномерному
закону в промежутке (0,1)randi([a,b],n,m) генерируют матрицу (n x m) с элементами в промежутке (a,b)
Слайд 35
Операции над матрицами
a+b сложение скаляров, векторов или матриц
a−b
вычитание скаляров, векторов или матриц
a*b умножение скаляров; матричное умножение
a.*b
покомпонентное умножение элементов матрицa^b возведение скаляра или матрицы в степень
a.^b возведение каждого элемента матрицы в степень
a/b деление скаляров;правое деление матриц, a · b−1
a./b покомпонентное деление элементов матриц
a\b левое деление матриц, т. е. a−1 · b
A’ транспонирование матрицы
Слайд 36
Операции над матрицами
Функция length(V) рассчитывает количество элементов в
векторе V.
Функция max(V) выдает значение максимального по значению элемента
вектора V. Функция min(V) извлекает минимальный элемент вектора V.
Функции mean(V) и std(V) определяют, соответственно, среднее значение и среднеквадратическое отклонение вектора V.
Слайд 37
Операции над матрицами
Функция сортировки sort(V) формирует вектор, элементы
которого распределены в порядке возрастания их значений.
Функция sum(V) вычисляет
сумму элементов вектора V.Функция prod(V) выдает произведение всех элементов вектора V.
Функция cumsum(V) формирует вектор того же типа и размера, любой элемент которого является суммой всех предыдущих элементов вектора V (вектор кумулятивной суммы).
Слайд 38
Операции над матрицами
abs(A) - модуль
det(A)
- определитель матрицы
inv(A) - обратная матрица
diag(A)
- главная диагональ матрицыsum(A) - сумма по столбцам (sum(A,1))
sum(A,2) - сумма по строкам
sum(diag(A)) - след матрицы
trace(A) - след матрицы
S=sum(sum(A)) - сумма матрицы
Слайд 39
Операции над матрицами
prod(A,1) - произведение элементов
массива в столбцах (по умолчанию prod(A))
prod(A,2)
- произведение элементов массива в строках sum(A') - сумма столбцов транспонированной матрицы
Слайд 40
Операции над матрицами
sort(A) - сортировка по столбцам
по возрастанию
sort(A,2) -сортировка по строкам по возрастанию
sort(A,’descend’)
- сортировка по столбцам по убыванию-sort(-A,2) - сортировка по строкам по убыванию
Слайд 41
Операции над матрицами
[b2,INDEX]=sort(b) - возвращает отсортированный массив и
массив индексов элементов в исходном массиве
size(A)
- размерность матрицыmax(A) - возвращает наибольший элемент, если А –вектор, или возвращает вектор-строку, содержащую максимальные элементы каждого столбца, если А -матрица
max(A,[ ],n) - возвращает наибольший элемент по столбцам при n=1, по строкам при n=2
min(A,[ ],n) - возвращает наименьший элемент по столбцам при n=1, по строкам при n=2
Слайд 42
Дневник работы
Команда diary
открывает дневник, т.е. указывает
системе, что все, что появится после этой команды на
экране до следующей команды diary будет записано в упомянутый текстовый файл.Прерывает запись в дневник команда открытия нового дневника или команда
diary off
Слайд 43
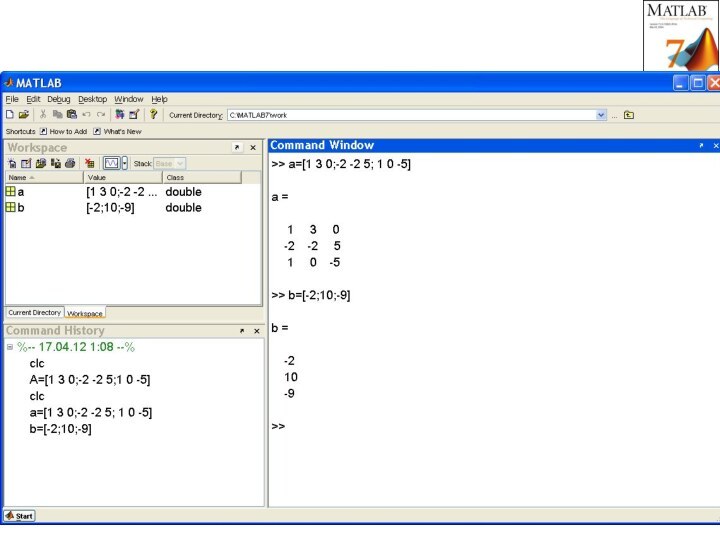
Решение системы линейных уравнений.
В матричном виде система имеет
вид
Ах =b,
A , b , х – матрицы
из коэффициентов при незвестных и вектор-столбцы, составленные соответственно из свободных членов и из неизвестных.
Слайд 46
Решение системы линейных уравнений
Решение x1=1, x2=-1, x3=2 легко
проверить подстановкой в систему уравнений:
>> disp(A*x)
-2.0000
10.0000-9.0000
В результате получен вектор-столбец свободных членов. Система решена верно.