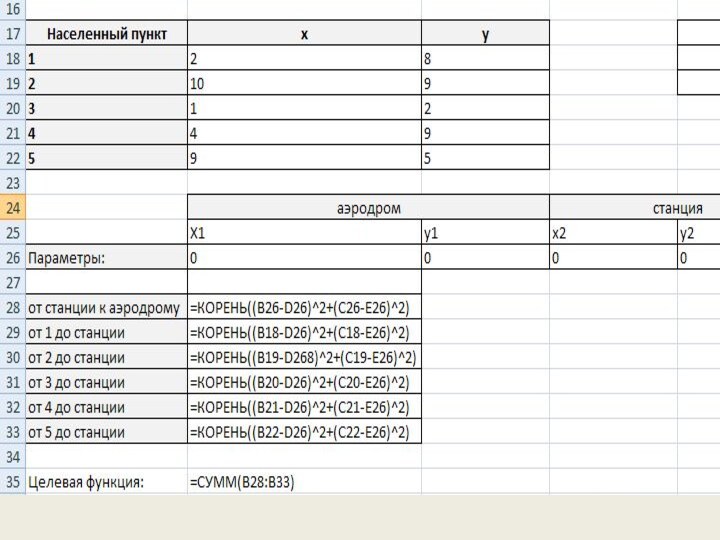
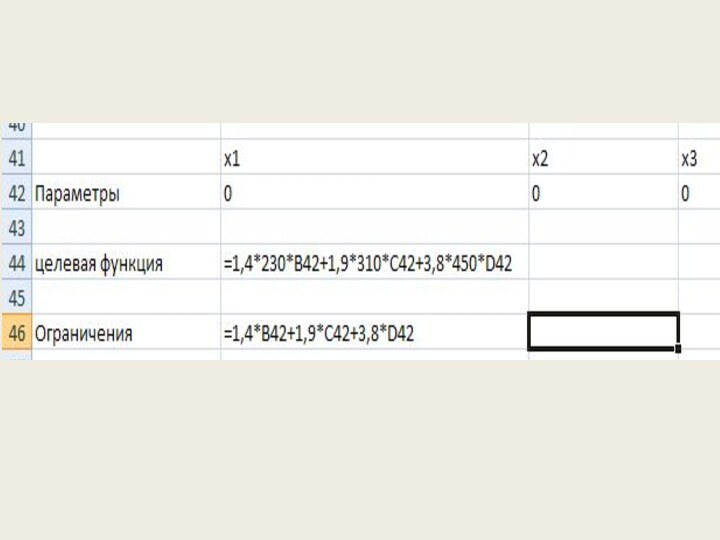
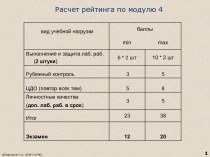
Excel, нужно установить надстройку Поиск решения:
Кнопка “Office” – Параметры
ExcelВ окне «Параметры Excel» слева выбрать пункт Надстройки, справа - пункт «Поиск решения», нажать на кнопку «Перейти».
Поставить галочку «Поиск решения» и нажать «ОК».