Слайд 2
Zalecana Literatura
Dasgupta S., Papadimitriou Ch., Vazirani U. Algorytmy
Wirth N.
Algorytmy+ struktury danych=programy Corman H. i inni Wprowadzenie do
algorytmów
Banachowski L. i inni Algorytmy i struktury danych
Sysło M.M. Algorytmy
Слайд 3
Algorytmy i struktury danych – AiSD
jako moduł/przedmiot
kształcenia na WSEI
Moduł AiDS jest adresowany do studentów
posiadających podstawową wiedzę o konstruowaniu programów i potrafiących programować w co najmniej jednym języku programowania: Pascal, C lub C++.
Celem wykładu jest zapoznanie studentów zarówno z klasycznymi zagadnieniami algorytmiki jak i gotowymi rozwiązaniami problemów spotykanych w codziennej pracy programistów i projektantów oprogramowania.
Programowanie komputerów uczy logicznego i algorytmicznego myślenia, systematycznego postępowania przy rozwiązywaniu problemów oraz wyrabia nawyki użyteczne przy rozwiązywaniu problemów nie tylko komputerowych.
Слайд 4
Efekty kształcenia w zakresie AiSD
Student po zaliczeniu przedmiotu
powinien:
Posiadać wiedzę dotyczącą:
algorytmów oraz zasad ich analizy i
metod układania,
podstawowych i złożonych struktur danych.
Potrafić oszacować złożoność obliczeniową i pamięciową algorytmu (programu komputerowego).
Posiadać umiejętność
efektywnego używania gotowych kontenerów
i algorytmów dostępnych w popularnych bibliotekach,
układania nieskomplikowanych algorytmów np.: obliczeniowych, sortowania, itd.,
implementacji zaawansowanych algorytmów.
Слайд 5
Pojęcie słowa „algorytm”
Intuicyjnie:
Algorytm jako przepis, proces, metoda, technika,
procedura.
Przykłady: przepis kucharski, instrukcja składania mebla/urządzenia/, zapis nutowy,
wykonywanie pisemne
dodawania/mnożenia/dzielenia
Precyzyjniej:
Algorytm – skończony zbiór reguł wskazujący kolejność operacji
dla rozwiązania problemu danego typu.
Sposób postępowania (przepis) umożliwiający rozwiązanie określonego zadania
(klasy zadań), podany w postaci skończonego zestawu czynności do wykonania,
ze wskazaniem ich następstwa.
Слайд 6
Istotne cechy algorytmu
Definicja zadania = co algorytm ma
zrobić
Opis ciągu czynności, które po kolei mają być wykonane
Czynności
te muszą być na tyle proste (i możliwe do wykonania), aby wykonawca algorytmu mógł je bez dodatkowego tłumaczenia, wykonać (operacje elementarne, odpowiednio dobrany poziom szczegółowości)
Skończona liczba operacji elementarnych (skończony czas działania)
Algorytm dostaje pewne informacje (dane wejściowe) i zwraca pewne (oczekiwane) wyniki — dane wyjściowe
Może istnieć kilka przepisów, które dają w wyniku te same wyniki
Слайд 7
Algorytm
Pochodzenie nazwy od nazwiska w wersji łacińskiej Algorithmus,
Algorismus, perskiego matematyka Muhammeda ibn Musy zwanego al Chuwarismi,
żyjącego w IX w; podał on algorytmy wykonywania działań arytmetycznych na liczbach dziesiętnych
Algorytmika – dział wiedzy zajmujący się badaniem algorytmów
Sposoby zapisu algorytmu
słowami
za pomocą schematu blokowego
w pseudokodzie
w jednym z języków programowania
Formalnie spisana wersja algorytmu to program
Слайд 9
Algorytm – formalnie
Cechy dobrego algorytmu
Skończoność. Wykonanie algorytmu
zawsze kończy się po
skończonej liczbie kroków.
Poprawne zdefiniowanie. Każdy krok
algorytmu opisany jest
precyzyjnie i jednoznacznie.
Dane wejściowe. Są to wartości znane przed rozpoczęciem
działania algorytmu lub dostarczane w czasie jego wykonywania.
Dane wyjściowe – wynik działania algorytmu. Algorytm generuje
dane wyjściowe, powiązane w pewien sposób z danymi
wejściowymi.
Efektywne zdefiniowanie. Operacje algorytmu powinny być
jak najprostsze, dające wykonać się w jak najkrótszym
możliwym czasie.
Def. Algorytm
ściśle określony ciąg kroków obliczeniowych, prowadzący do przekształcenia danych wejściowych w wyjściowe
Слайд 10
Zadanie algorytmiczne (obliczeniowe)
Postawienie problemu (specyfikacja zadania algorytmicznego)
Dane wejściowe
— poprawność i zakres danych wejściowych
Dane wyjściowe (wyniki) —
charakterystyka oczekiwanych wyników jako funkcji danych wejściowych
Celem zadania algorytmicznego jest znalezienie algorytmu przekształcającego dane wejściowe w wyjściowe, zgodnie z zadanymi założeniami
Algorytm = rozwiązanie zadania algorytmicznego
Algorytm powinien działać dla dowolnego zestawu danych ze zbioru poprawnych danych wejściowych
Слайд 11
Dobry algorytm –
warunek konieczny, ale nie wystarczający
napisania poprawnego i wydajnego programu
Rozwiązywanie problemu (zagadnienia),
projektowanie algorytmu
Modelowanie
rzeczywistości:
zdefiniowanie zadania
wprowadzenie założeń i ograniczeń
selekcja informacji
Algorytm rozwiązania
Zapis:
w języku naturalnym
pseudokod
schemat blokowy
Wybór narzędzia programowania
Implementacja
struktur danych
algorytmu rozwiązania
Слайд 12
Konstruowanie algorytmu
Definicja problemu (najlepiej w postaci modelu matematycznego)
Koncepcja
rozwiązania i wybór struktur danych
Zapis algorytmu (stopniowe precyzowanie od
koncepcji do pseudo-kodu lub kodu)
Dowód poprawności i analiza złożoności obliczeniowej
Implementacja w wybranym języku programowania
Слайд 13
Klasy algorytmów
Rekursja
Metoda „dziel i zwyciężaj”
Algorytmy
zachłanne
Programowanie dynamiczne
Algorytmy redukcyjne
Klasy zadań algorytmicznych
Dziel i
zwyciężaj (ang. divide and conquer) – jedna z głównych metod projektowania algorytmów w informatyce, prowadząca do bardzo efektywnych rozwiązań. Nazwa pochodzi od łacińskiej sentencji dziel i rządź (łac. divide et impera). W strategii tej problem dzieli się rekurencyjnie na dwa lub więcej mniejszych podproblemów tego samego (lub podobnego) typu tak długo, aż fragmenty staną się wystarczająco proste do bezpośredniego rozwiązania (np. QuickSort).
Algorytm zachłanny (ang. greedy algorithm) – algorytm, który w celu wyznaczenia rozwiązania w każdym kroku dokonuje zachłannego, tj. najlepiej rokującego w danym momencie wyboru rozwiązania częściowego (Algorytm Kruskala, Algorytm Dijkstry )
Слайд 14
Analiza algorytmów
Analiza algorytmów polega na zdefiniowaniu zasobów niezbędnych
do
jego wykonania
Przykłady zasobów:
czas obliczeń
pamięć
pojemność kanału komunikacyjnego
układy logiczne (wejście - wyjście)
Слайд 15
Przykład algorytmu:
Zdefiniowanie problemu
Zaplanowano zorganizowanie trzech spotkań premiera
z
mieszkańcami (17; 25; 49) miast.
Należy wskazać premierowi najkrótszą drogę
(w każdym z trzech przypadków), jeśli premier wyrusza
z Warszawy i w każdym z miast ma być dokładnie jeden raz
na końcu wrócić do stolicy.
Слайд 16
Analiza problemu
(danych, dostępnych narzędzi i środków);
wybór
metody rozwiązania
Dane: n- liczba miast (pierwsza stolica)
Wynik: ciąg
nazw n miast ustawiony według kryterium ”najkrótszej drogi” (pierwsza jest stolica)
Poszukiwanie metody rozwiązania: liczba możliwych uporządkowań zbioru (n-1) elementowego wynosi (n-1)!
Dostępne środki
Komputer wykonujący w ciągu 1 sek 100 000 000 000 operacji elementarnych (porównanie ciągów n elementowych)
Liczba miast Czas wykonania
17 3.5 minuty
25 2*105 lat
49 4*1042lat
Слайд 17
Analiza problemu
Weryfikacja przyjętej metody
Przeprowadzona analiza wskazuje, iż stosowanie
tej metody poszukiwania najlepszego rozwiązania już przy n=20, jest
nieefektywne, wręcz niewykonalne w rozsądnym czasie.
Слайд 18
Analiza zadania,
Definiowanie problemu
Uporządkować rosnąco zbiór danych liczbowych
Analiza
problemu wybór metody rozwiązania:
porządkowanie przez wybór
porządkowanie bąbelkowe
porządkowanie metodą dziel
i zwyciężaj
porządkowanie przez wstawianie
Opracowanie algorytmu
Algorytmy to temat wykładu
Слайд 19
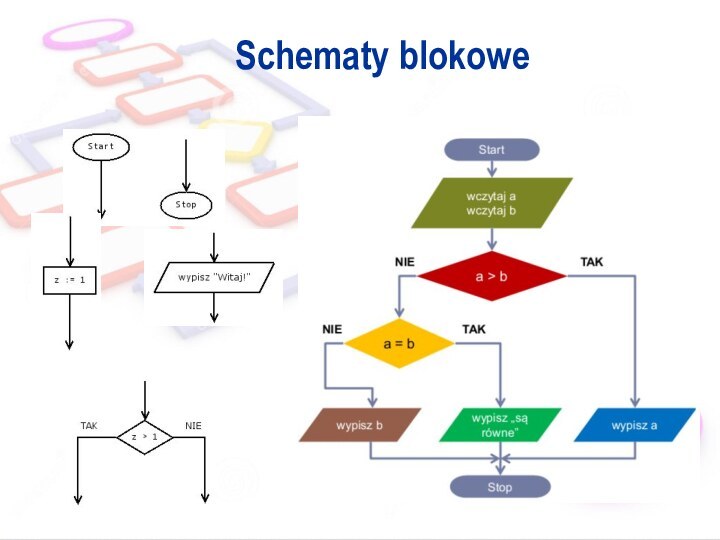
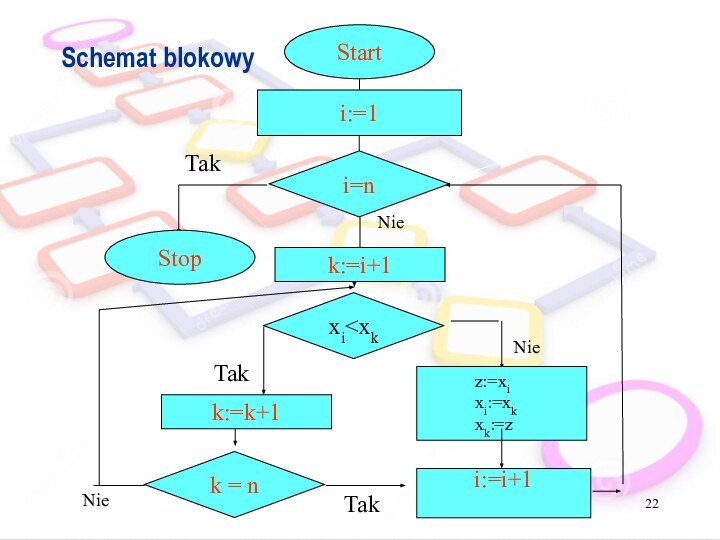
Sposoby przedstawiania algorytmów
Opis słowny
Lista kroków ( czynności następujących
w określonej kolejności)
Schemat blokowy
Drzewo algorytmu
Pseudokod - lista instrukcji napisanych
w języku programowania.
Слайд 20
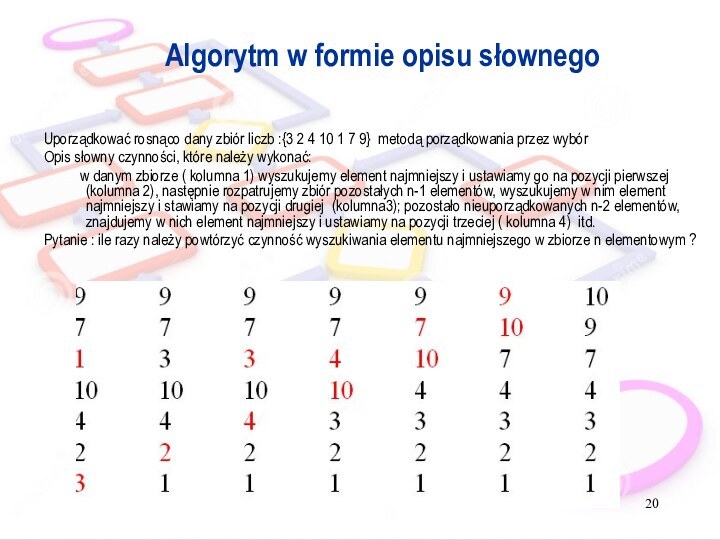
Algorytm w formie opisu słownego
Uporządkować rosnąco dany zbiór
liczb :{3 2 4 10 1 7 9} metodą
porządkowania przez wybór
Opis słowny czynności, które należy wykonać:
w danym zbiorze ( kolumna 1) wyszukujemy element najmniejszy i ustawiamy go na pozycji pierwszej (kolumna 2), następnie rozpatrujemy zbiór pozostałych n-1 elementów, wyszukujemy w nim element najmniejszy i stawiamy na pozycji drugiej (kolumna3); pozostało nieuporządkowanych n-2 elementów, znajdujemy w nich element najmniejszy i ustawiamy na pozycji trzeciej ( kolumna 4) itd.
Pytanie : ile razy należy powtórzyć czynność wyszukiwania elementu najmniejszego w zbiorze n elementowym ?
Слайд 21
Lista kroków
Dane: zbiór liczb: {x1,x2, …,xn}
Wynik : uporządkowany
ciąg liczb: x1
kroki 2,3
K2: Znajdź k, takie, że xk jest najmniejszym elementem w podciągu xi, xn
K3: Zamień miejscami xi oraz xk.
Слайд 23
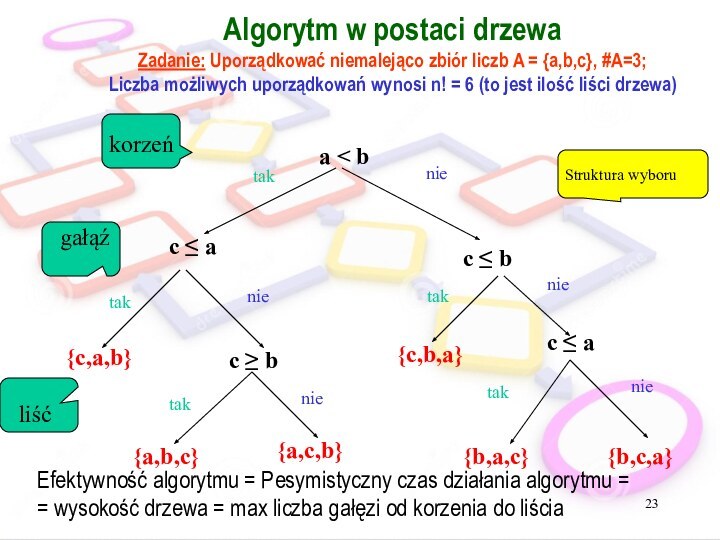
Algorytm w postaci drzewa
Zadanie: Uporządkować niemalejąco zbiór liczb
A = {a,b,c}, #A=3;
Liczba możliwych uporządkowań wynosi n!
= 6 (to jest ilość liści drzewa)
a < b
c ≤ a
c ≤ b
c ≥ b
c ≤ a
{c,a,b}
{a,b,c}
{a,c,b}
{c,b,a}
{b,a,c}
{b,c,a}
tak
tak
tak
tak
tak
nie
nie
nie
nie
nie
liść
gałąź
korzeń
Efektywność algorytmu = Pesymistyczny czas działania algorytmu =
= wysokość drzewa = max liczba gałęzi od korzenia do liścia
Struktura wyboru
Слайд 24
Pseudokod
Konwencje stosowane w pseudokodzie
Stosuje się wcięcia i zapisy
odpowiadające strukturze blokowej
warunek if-then- else
pętle ( jak w Pascalu)
while
for
repeat
komentarz jest wewnątrz nawiasów {.……..}
przypisanie zmiennej x wartości j x← j
wielokrotne przypisanie zmiennym i oraz j wartości wyrażenia e i← j←e
A[i] oznacza i-ty element tablicy A
A[1..j] podtablica tablicy A, zawierająca elementy A[1], A[2],.....A[j]
Lenght [A] dane złożone z kilku części organizowane są jako obiekty, składające się z atrybutów lub pól.
Obiekt np. tablica A ma atrybut lenght oznaczający liczbę jej elementów
Zmienna odpowiadająca tablicy lub obiektowi jest traktowana jako wskaźnik do danych reprezentujących tę tablicę lub obiekt.
Dla wszystkich pól f obiektu x, przypisanie y← x wskazuje na te same obiekty ( są tymi samymi obiektami, powoduje f[x] = f[y],
Jeśli wykonamy f[x] ← x to f [x] = 3 i f [y] = 3
Слайд 25
Projektowanie algorytmów
„Projektowanie programów poprawnych i dobrze zbudowanych"
(Alagić S.,Arbib M.A.-WNT 1982)
....polega na rozłożeniu zadania na
ściśle określone podzadania, których poprawne rozwiązanie i właściwe ich połączenie da rozwiązanie całego problemu .
"Things should be as simple
as possible but no simpler.” Albert Einstein