- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Десятая Всероссийская командная олимпиада школьников по программированию
Содержание
- 2. Задача A. Поедание сыра
- 3. Авторы задачиАвтор задачи — Сергей МельниковУсловие — Андрей СтанкевичПодготовка тестов — Антон АхиРазбор — Сергей Мельников
- 4. Общая идеяИспользуем двоичный поиск по ответуДано t,
- 5. Интересные интервалыПусть Ti – все моменты времени
- 6. Скорости всех мышей равны 1Рассмотрим сетьВ ней
- 7. Скорости всех мышей равны 1Три сыраp1=1 r1=2 d1=2p2=3 r2=1 d2=4p3=2 r3=2 d3=4Две мыши
- 8. Разные скорости мышейУпорядочим мышей по неубыванию скоростей:s1
- 9. Модификация сетиРаньше былоЗаменим, на такой фрагментKj,k – одни и те же разных i и одного Ik
- 10. Общее решениеДвоичный поискПоток в специальной сети
- 11. Спасибо за внимание! Вопросы по задаче A?
- 12. Задача B. Соревнования по программированию
- 13. Авторы задачиАвтор задачи — Владимир УльянцевУсловие — Федор ЦаревПодготовка тестов — Антон АхиРазбор — Антон Ахи
- 14. О чем задача?Дан список файлов и определения
- 15. Как решать?Востановить полностью дерево каталогов и файловИспользовать
- 16. Как посчитать количество описаний соревнований?В получившемся дереве
- 17. Сколько работает?Во входном файле задано не более 100000 файлов/каталоговКаждый каталог просматривается один раз
- 18. Спасибо за внимание! Вопросы по задаче B?
- 19. Задача C. Распил
- 20. Авторы задачиАвторы задачи — Елена Андреева, Владимир ГуровицУсловие — Андрей СтанкевичПодготовка тестов — Антон БанныхРазбор — Антон Банных
- 21. О чем задача?Придумать n-угольник, который можно распилить
- 22. Какие n, m, k допустимы?Если
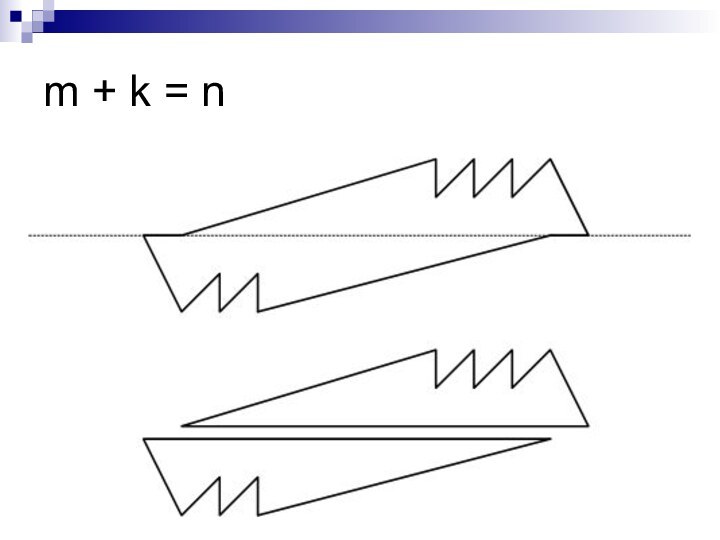
- 23. m + k = n
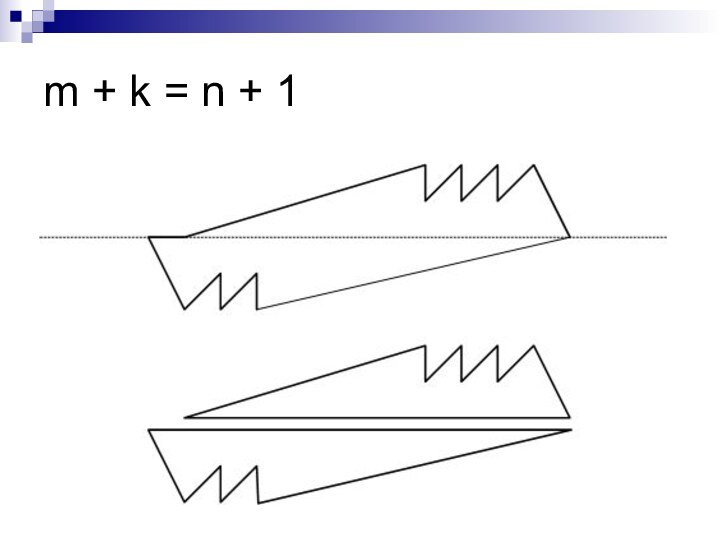
- 24. m + k = n + 1
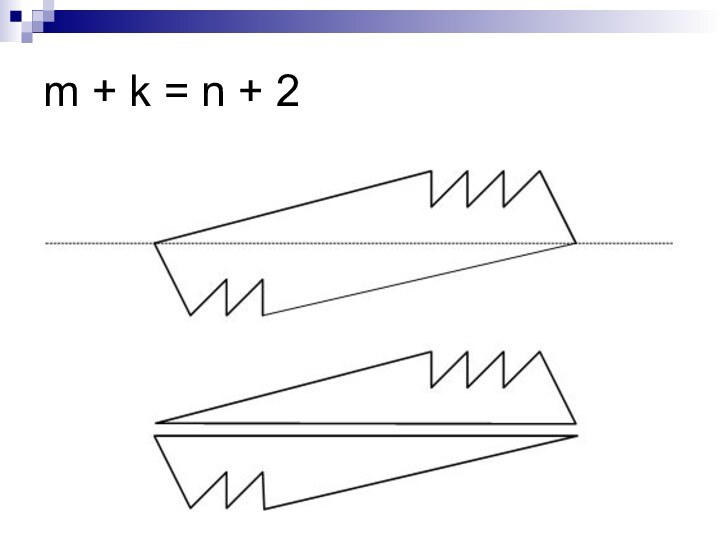
- 25. m + k = n + 2
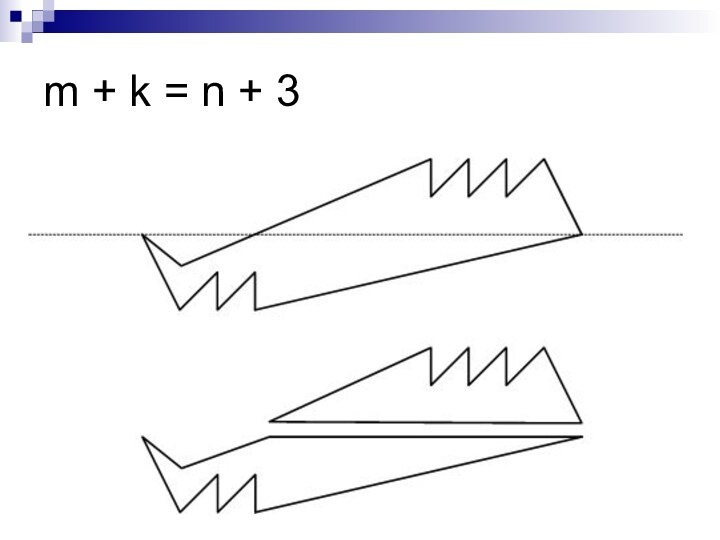
- 26. m + k = n + 3
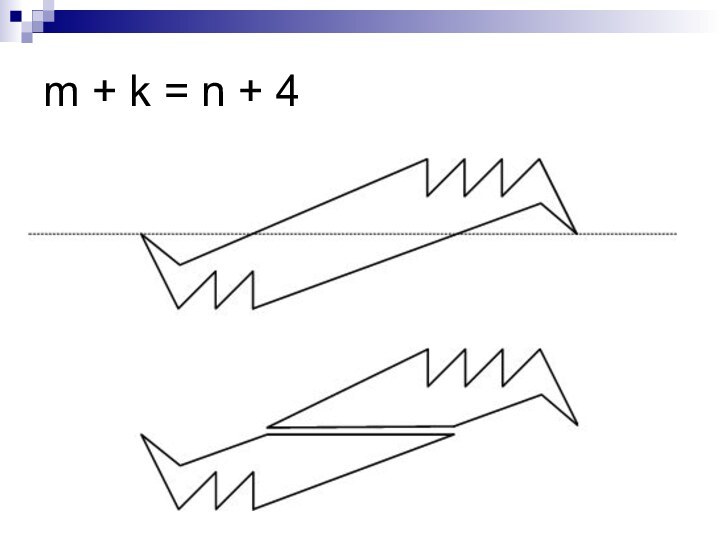
- 27. m + k = n + 4
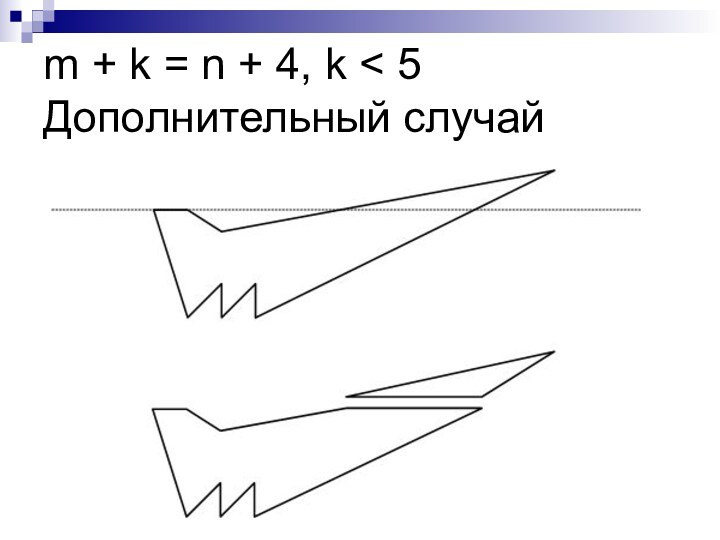
- 28. m + k = n + 4, k < 5 Дополнительный случай
- 29. Спасибо за внимание! Вопросы по задаче C?
- 30. Задача D. Электричество
- 31. Авторы задачиАвтор задачи — Владимир ГуровицУсловие — Федор ЦаревПодготовка тестов — Сергей ПоромовРазбор — Антон Банных
- 32. О чем задача?В наличии:k сетевых фильтровn элетроприборов1
- 33. Основные идеиНе имеет смысла поключать фильтр к
- 34. РешениеОтсортировать электроприборы и фильтры в порядке невозрастания мощностей.Строить ответ жадно, начиная с фильтра, подключенного к розетке.
- 35. Спасибо за внимание! Вопросы по задаче D?
- 36. Задача E. Адронные коллайдеры
- 37. Авторы задачиАвтор задачи — Михаил КеверУсловие — Федор ЦаревПодготовка тестов — Сергей ПоромовРазбор — Сергей Мельников
- 38. Две окружностиДве окружности: найдем окружность с центром на прямой, соединяющей центры исходных окружностей
- 39. Две окружностиДля любой точки С на перпендикуляре восстановленном в точке D – существует окружность являющаяся решением
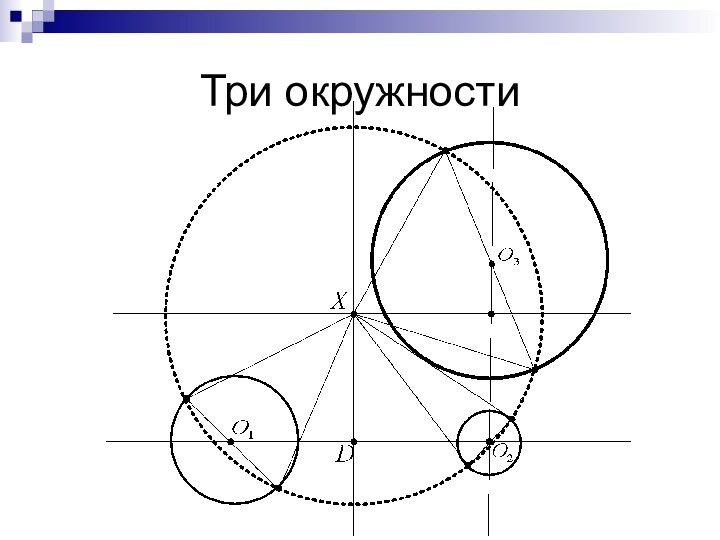
- 40. Три окружностиТри окружности:Построим прямую на которой может
- 41. Три окружности
- 42. Спасибо за внимание! Вопросы по задаче E?
- 43. Задача F. Космические захватчики
- 44. Авторы задачиАвтор задачи — Георгий КорнеевУсловие — Павел МавринПодготовка тестов — Антон БанныхРазбор — Антон Ахи
- 45. О чем задача?В столбцах находятся ai захватчиковПушка
- 46. Частный случай Если пушка стоит в крайнем
- 47. РешениеДойти до ближайшего из краев, далее действовать по предыдущему плануОтвет — Σai+(n-1)+min(p-1,n-p)
- 48. Спасибо за внимание! Вопросы по задаче F?
- 49. Задача G. Пробежки по Манхэттену
- 50. Авторы задачиАвтор задачи — Михаил ДворкинУсловие — Павел МавринПодготовка тестов — Олег ДавыдовРазбор — Михаил Дворкин
- 51. О чем задача?Объект передвигается по Манхэттену, пробегая
- 52. УтверждениеВ каждый момент времени множество точек, в
- 53. В начальный момент времениЭто точка (0, 0) — вырожденный прямоугольник.
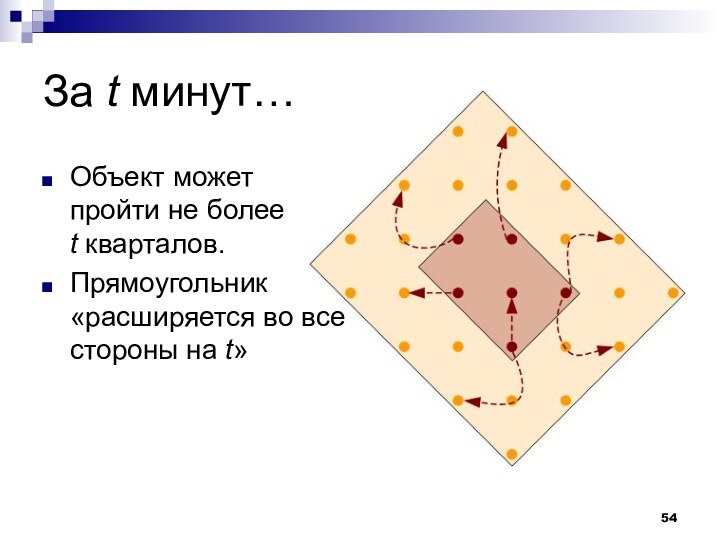
- 54. За t минут…Объект может пройти не более t кварталов. Прямоугольник «расширяется во все стороны на t»
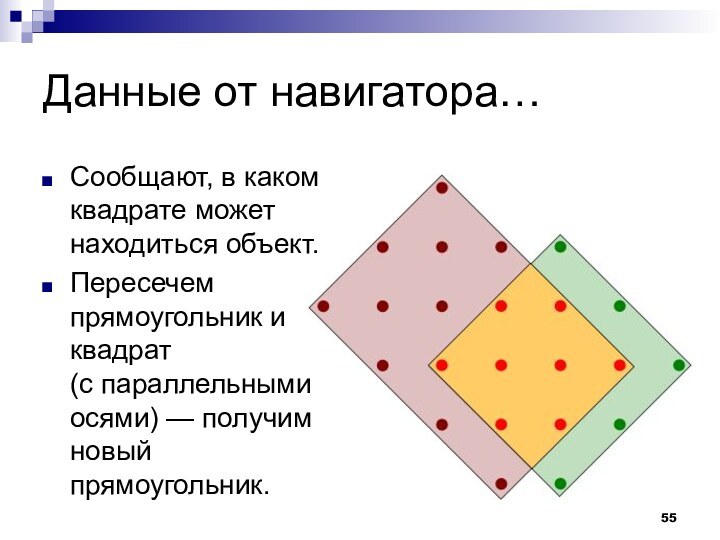
- 55. Данные от навигатора…Сообщают, в каком квадрате может
- 56. Спасибо за внимание! Вопросы по задаче G?
- 57. Задача H. Следующее разбиение на слагаемые
- 58. Авторы задачиАвтор задачи — Андрей СтанкевичУсловие — Андрей СтанкевичПодготовка тестов — Сергей МельниковРазбор — Сергей Мельников
- 59. Генерация следующего комбинаторного объектаДано разбиение5=1+1+3Идём с конца,
- 60. Когда можно увеличить слагаемое?Первое слагаемое с конца
- 61. На сколько можно увеличить слагаемое?Слагаемое можно увеличить
- 62. Минимальный «хвост»?Надо вывести хвост с суммой S,
- 63. Спасибо за внимание! Вопросы по задаче H?
- 64. Задача I. Самодвойственный документ
- 65. Авторы задачиАвтор задачи — Сергей МельниковУсловие — Андрей СтанкевичПодготовка тестов — Сергей МельниковРазбор — Сергей Мельников
- 66. Условие задачиВ задаче надо построить граф из
- 67. Когда ответ существует?В полном графе из n
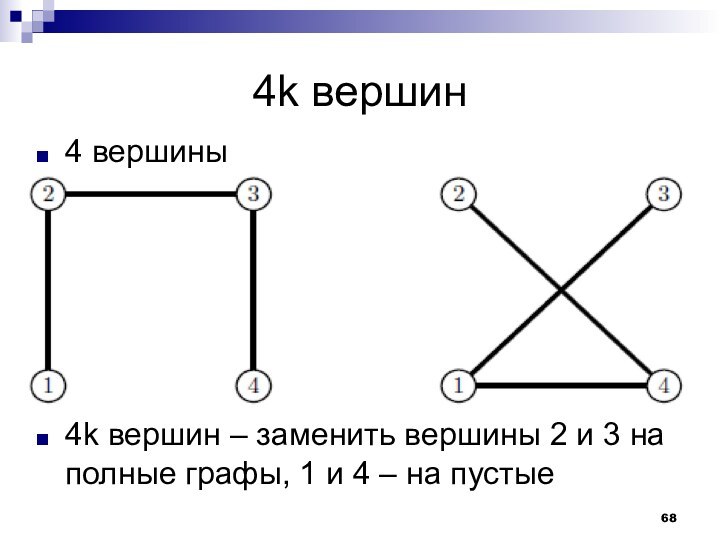
- 68. 4k вершин4 вершины4k вершин – заменить вершины
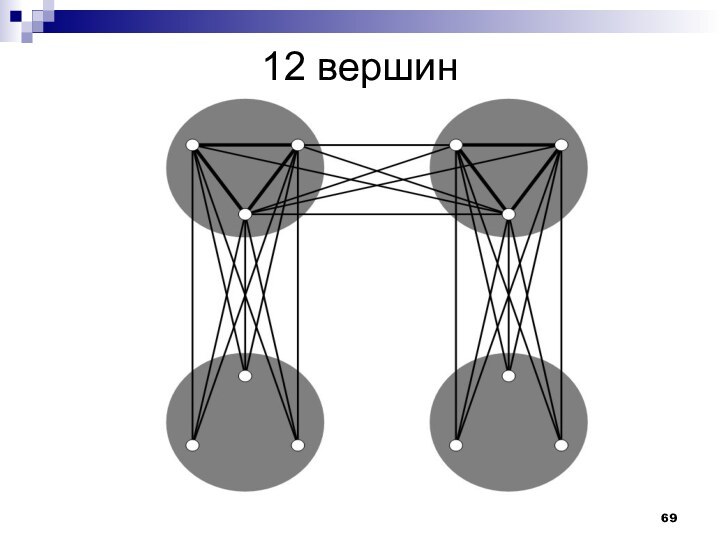
- 69. 12 вершин
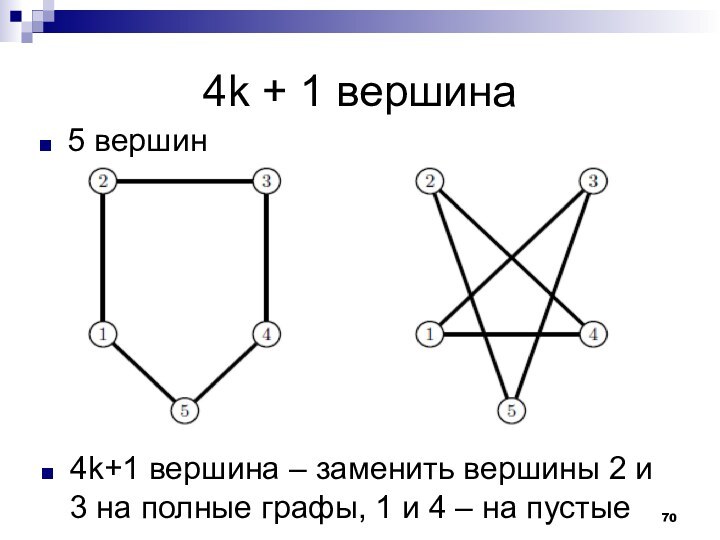
- 70. 4k + 1 вершина4k+1 вершина – заменить
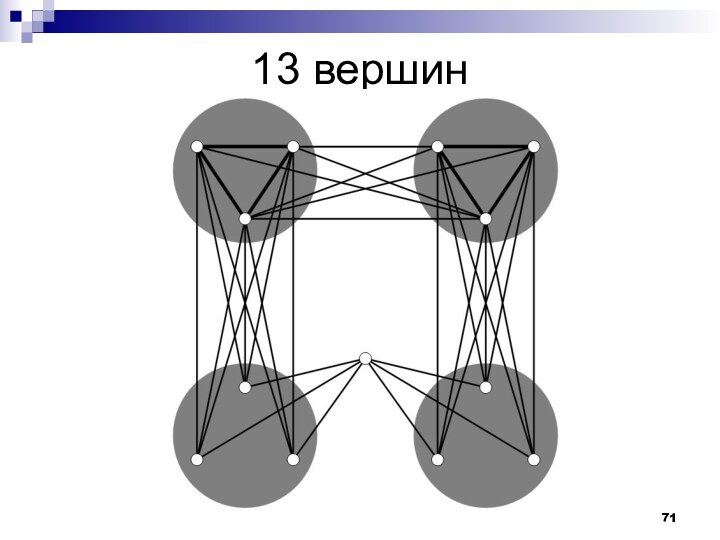
- 71. 13 вершин
- 72. Спасибо за внимание! Вопросы по задаче I?
- 73. Задача J. Цирковое шоу
- 74. Авторы задачиАвтор задачи — Юрий ПетровУсловие — Павел МавринПодготовка тестов — Юрий ПетровРазбор — Юрий Петров
- 75. ФормулировкаДан набор отрезковВыбрать два поднабора, объединения которых не пересекаютсяМаксимизировать минимум размеров
- 76. Идея решенияДинамическое программирование
- 77. Решение: вычисляемая функцияФункция f(a, n, t):a — самый
- 78. Решение: переходыПеребрать отрезок b, который будет завершать
- 79. Оценка времени работыВсего есть n×n×2 состоянийИз каждого
- 80. Спасибо за внимание! Вопросы по задаче J?
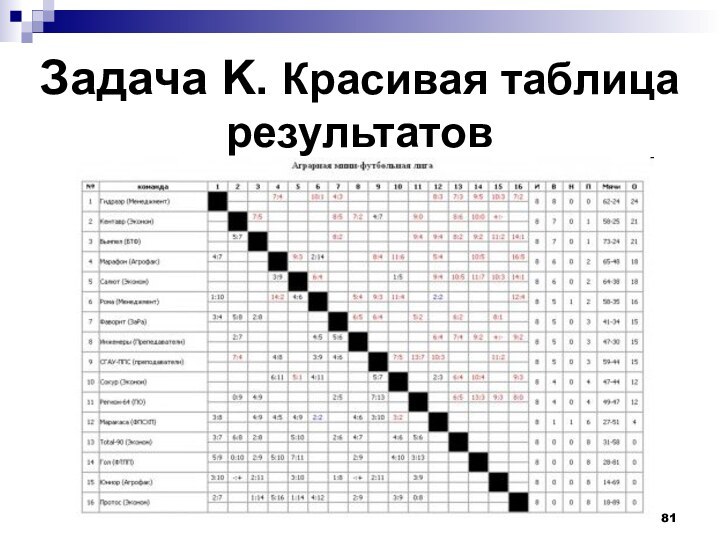
- 81. Задача K. Красивая таблица результатов
- 82. Авторы задачиАвтор задачи — Владимир УльнцевУсловие — Андрей СтанкевичПодготовка тестов — Владимир УльянцевРазбор — Антон Ахи
- 83. О чем задача?Таблица результатов считается красивой, если
- 84. Как решать?Для каждой команды увеличивать количество сданных
- 85. Скачать презентацию
- 86. Похожие презентации
Задача A. Поедание сыра


































































Слайд 3
Авторы задачи
Автор задачи — Сергей Мельников
Условие — Андрей Станкевич
Подготовка тестов —
Антон Ахи
Слайд 4
Общая идея
Используем двоичный поиск по ответу
Дано t, можно
ли организовать поедание сыра, чтобы мыши не ели сыр
более чем через t часов, после того как сыр начал портитсяОбозначим Di = di + t
Слайд 5
Интересные интервалы
Пусть Ti – все моменты времени ri
и Di
T1 < T2 < … < Tn
Время
разбивается на интервалы [Ti, Ti+1]Сыр или можно есть в течение всего интервала, или нельзя
Слайд 6
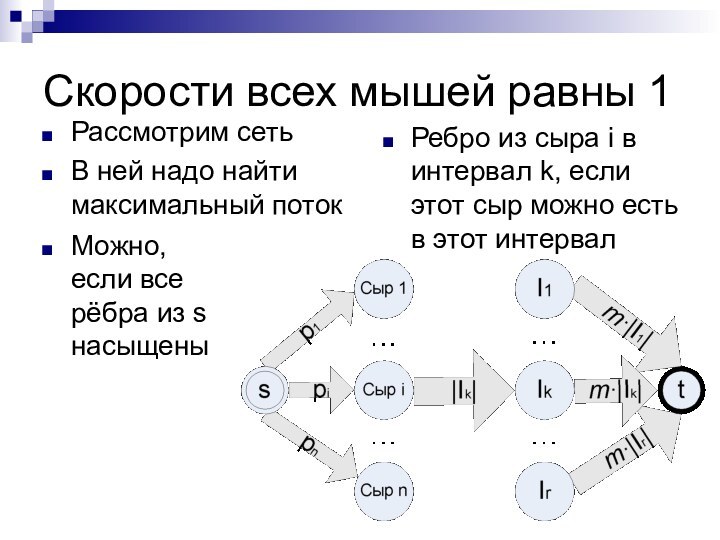
Скорости всех мышей равны 1
Рассмотрим сеть
В ней надо
найти максимальный поток
Ребро из cыра i в интервал k,
если этот сыр можно есть в этот интервалМожно, если все рёбра из s насыщены
Слайд 8
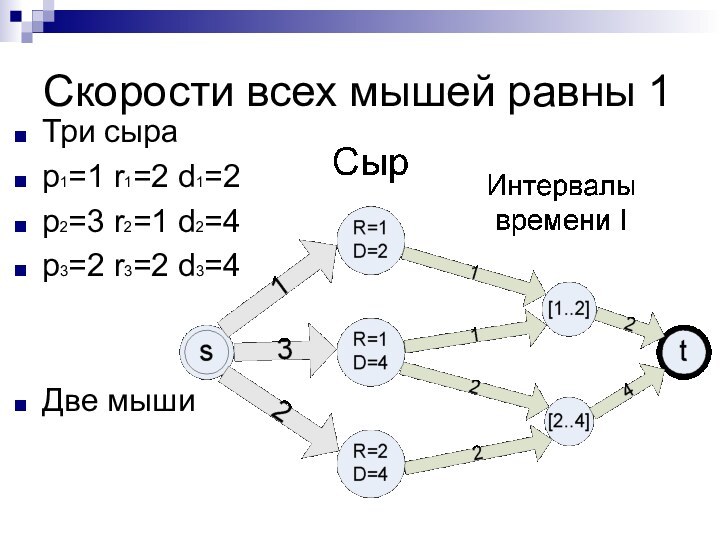
Разные скорости мышей
Упорядочим мышей по неубыванию скоростей:
s1 ≥
s2 ≥ … ≥ sm
Представим (m-1)-ю мышь, как
набор из мыши со скоростью sm, и мыши со скоростью sm-1-sm Аналогично разобьем (m-2)-ю мышь на 3 три мыши: sm, sm-1-sm и sm-2-sm-1
И так далее
Слайд 9
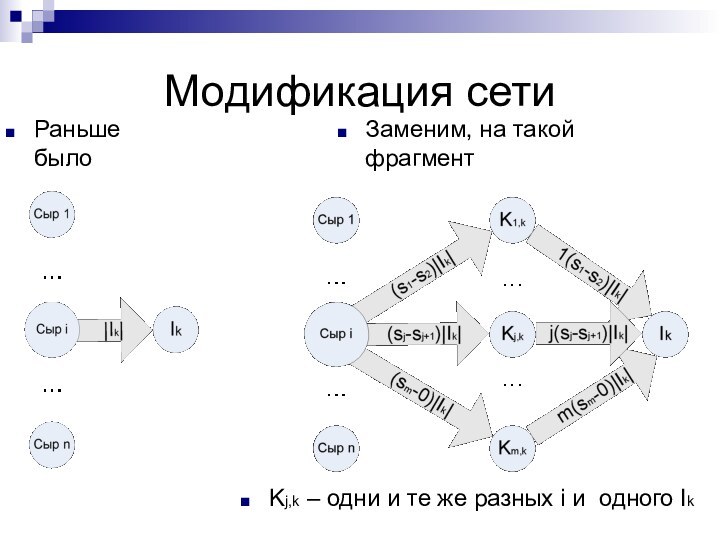
Модификация сети
Раньше было
Заменим, на такой фрагмент
Kj,k – одни
и те же разных i и одного Ik
Слайд 13
Авторы задачи
Автор задачи — Владимир Ульянцев
Условие — Федор Царев
Подготовка тестов —
Антон Ахи
Разбор — Антон Ахи
Слайд 14
О чем задача?
Дан список файлов и определения для
каталогов с тестами, задач и описаний соревнований
Необходимо посчитать количество
описаний соревнаваний
Слайд 15
Как решать?
Востановить полностью дерево каталогов и файлов
Использовать символ
«\» как разделитель имен в путях
Для каждого каталога хранить
список подкаталогов и файлов в нем, например с помощью хеш-таблицы
Слайд 16
Как посчитать количество описаний соревнований?
В получившемся дереве файлов/каталогов
проверить про каждый каталог, является ли он каталогом с
тестами, задачей или описанием соревнованийНе зыбыть, что в каталоге с тестами могут быть подкаталоги
Слайд 17
Сколько работает?
Во входном файле задано не более 100000
файлов/каталогов
Каждый каталог просматривается один раз
Слайд 20
Авторы задачи
Авторы задачи — Елена Андреева, Владимир Гуровиц
Условие — Андрей
Станкевич
Подготовка тестов — Антон Банных
Разбор — Антон Банных
Слайд 21
О чем задача?
Придумать n-угольник, который можно распилить на
k-угольник и m-угольник разрезом, проходящим через две его вершины.
Слайд 22
Какие n, m, k допустимы?
Если
,
решения нет.Иначе при достаточно больших n, m, k искомый многоугольник существует.
Слайд 31
Авторы задачи
Автор задачи — Владимир Гуровиц
Условие — Федор Царев
Подготовка тестов —
Сергей Поромов
Разбор — Антон Банных
Слайд 32
О чем задача?
В наличии:
k сетевых фильтров
n элетроприборов
1 розетка
Требуется
подсоединить все элетроприборы так, чтобы потребляемая ими мощность не
превышала допустимую для сетевого фильтра.К сетевому фильтру можно подсоединить не более одного сетевого фильтра.
Слайд 33
Основные идеи
Не имеет смысла поключать фильтр к фильтру
с меньшей максимальной нагрузкой.
Наиболее мощные приборы имеет смысл ставить
ближе к розетке.
Слайд 34
Решение
Отсортировать электроприборы и фильтры в порядке невозрастания мощностей.
Строить
ответ жадно, начиная с фильтра, подключенного к розетке.
Слайд 37
Авторы задачи
Автор задачи — Михаил Кевер
Условие — Федор Царев
Подготовка тестов —
Сергей Поромов
Разбор — Сергей Мельников
Слайд 38
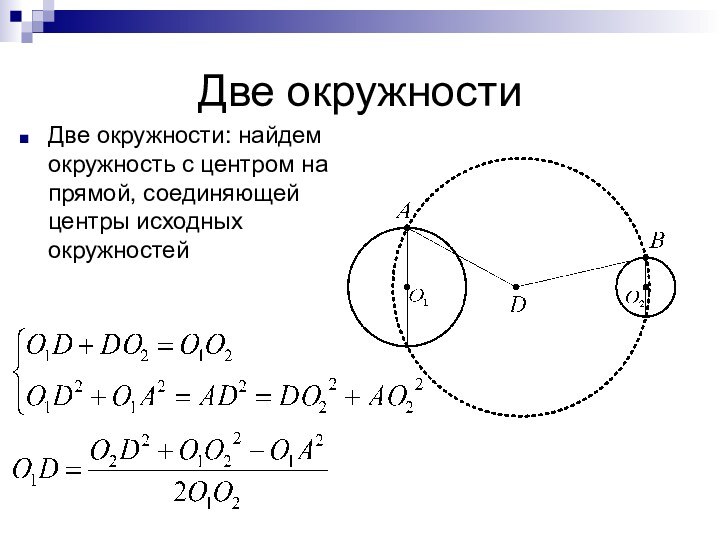
Две окружности
Две окружности: найдем окружность с центром на
прямой, соединяющей центры исходных окружностей
Слайд 39
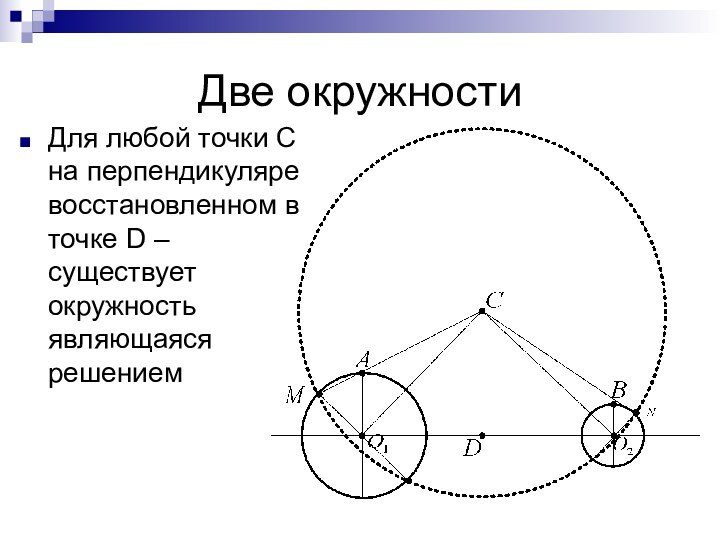
Две окружности
Для любой точки С на перпендикуляре восстановленном
в точке D – существует окружность являющаяся решением
Слайд 40
Три окружности
Три окружности:
Построим прямую на которой может быть
центр окружности делящей пополам O1 и O2
Построим прямую
на которой может быть центр окружности делящей пополам O2 и O3 Найдем их точку пересечения - X
Слайд 44
Авторы задачи
Автор задачи — Георгий Корнеев
Условие — Павел Маврин
Подготовка тестов —
Антон Банных
Разбор — Антон Ахи
Слайд 45
О чем задача?
В столбцах находятся ai захватчиков
Пушка за
одно действие либо перемещается в соседний столбец, либо производит
выстрел и убивает одного захватчикаНеобходимо уничтожить всех захватчиков за минимальное количество действий
Слайд 46
Частный случай
Если пушка стоит в крайнем столбце,
то нужно уничтожить всех захватчиков в этом столбце и
перейти к следующемуОтвет — сумма общего количества захватчиков и количества перемещений, то есть Σai+(n-1)
Слайд 47
Решение
Дойти до ближайшего из краев, далее действовать по
предыдущему плану
Ответ — Σai+(n-1)+min(p-1,n-p)
Слайд 50
Авторы задачи
Автор задачи — Михаил Дворкин
Условие — Павел Маврин
Подготовка тестов —
Олег Давыдов
Разбор — Михаил Дворкин
Слайд 51
О чем задача?
Объект передвигается по Манхэттену, пробегая за
t минут не более чем t кварталов.
Каждые t минут навигатор сообщает
точку, где находится объект, с точностью до d кварталов.Где может находиться объект в данный момент времени?
Слайд 52
Утверждение
В каждый момент времени множество точек, в которых
может находиться объект, составляют прямоугольник, стороны которого повернуты на
45° относительно осей координат.
Слайд 54
За t минут…
Объект может пройти не более t кварталов.
Прямоугольник «расширяется во все стороны на t»
Слайд 55
Данные от навигатора…
Сообщают, в каком квадрате может находиться
объект.
Пересечем прямоугольник и квадрат (с параллельными осями) — получим новый
прямоугольник.
Слайд 58
Авторы задачи
Автор задачи — Андрей Станкевич
Условие — Андрей Станкевич
Подготовка тестов —
Сергей Мельников
Разбор — Сергей Мельников
Слайд 59
Генерация следующего комбинаторного объекта
Дано разбиение
5=1+1+3
Идём с конца, пока
нельзя увеличить слагаемое
Увеличим слагаемое на минимальную величину
Допишем минимальный «хвост»
Слайд 60
Когда можно увеличить слагаемое?
Первое слагаемое с конца нельзя
увеличить
Второе слагаемое с конца можно увеличить
Например можно прибавить к
нему последнее слагаемое5=1+1+3 → 5=1+4
Слайд 61
На сколько можно увеличить слагаемое?
Слагаемое можно увеличить на
1, если оно было меньше последнего хотя бы на
25=1+1+3 → 5=1+2+2
Иначе его надо увеличить на величину последнего слагаемого
5=1+2+2 → 5=1+4
Слайд 62
Минимальный «хвост»?
Надо вывести хвост с суммой S, при
этом последнее слагаемое которое было выведено перед ним равно
KВыведем несколько(возможно ноль) слагаемых K, а затем остаток
Остаток должен быть не меньше чем K
Слайд 65
Авторы задачи
Автор задачи — Сергей Мельников
Условие — Андрей Станкевич
Подготовка тестов —
Сергей Мельников
Разбор — Сергей Мельников
Слайд 66
Условие задачи
В задаче надо построить граф из n
вершин
Первый отдел: пары чисел – это ребра графа
Второй отдел:
пары чисел – это вершины между которыми ребра нетГраф изоморфен своему дополнению
Слайд 67
Когда ответ существует?
В полном графе из n вершин
n(n - 1)/2 ребер
Если n = 4k + 2
или n = 4k + 3, то ребер нечетное число – ответ «No»Если n = 4k или n = 4k + 1, то ответ «Yes»
Слайд 70
4k + 1 вершина
4k+1 вершина – заменить вершины
2 и 3 на полные графы, 1 и 4
– на пустые5 вершин
Слайд 74
Авторы задачи
Автор задачи — Юрий Петров
Условие — Павел Маврин
Подготовка тестов —
Юрий Петров
Разбор — Юрий Петров
Слайд 75
Формулировка
Дан набор отрезков
Выбрать два поднабора, объединения которых не
пересекаются
Максимизировать минимум размеров
Слайд 77
Решение: вычисляемая функция
Функция f(a, n, t):
a — самый правый
из отрезков, взятых в один из наборов
n — текущее количество
отрезков в первом набореt — какому набору принадлежит отрезок a
Значение — максимальное количество отрезков во втором наборе
Слайд 78
Решение: переходы
Перебрать отрезок b, который будет завершать следующую
группу
Перебрать набор, в который взять эту группу
Все отрезки, лежащие
правее конца a и левее конца b, выгодно взять в тот же набор
Слайд 79
Оценка времени работы
Всего есть n×n×2 состояний
Из каждого O(n)
переходов
Переходы перебирать в порядке возрастания конца отрезка
Суммарное время обработки
переходов из одного состояния O(n)Итоговое время O(n3)
Слайд 82
Авторы задачи
Автор задачи — Владимир Ульнцев
Условие — Андрей Станкевич
Подготовка тестов —
Владимир Ульянцев
Разбор — Антон Ахи
Слайд 83
О чем задача?
Таблица результатов считается красивой, если количество
задач, решенных каждой из команд, либо 0, либо делитель
числа задач на соревнованииСколько еще можно сдать задач, чтобы таблица не переставала быть красивой