при котором функция в процессе выполнения входящих в ее
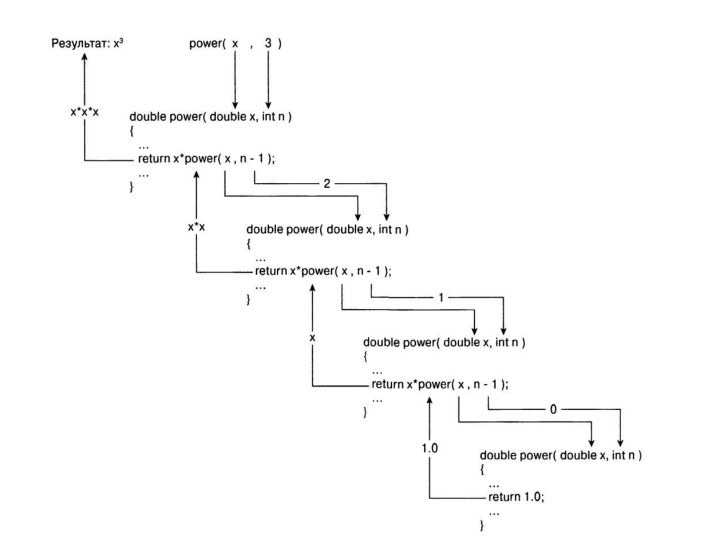
состав операторов обращается сама к себе непосредственно либо через другие функции.Рекурсивные функции (лат. recursio – возвращение) – в вычислительной математике – функции, определенные на множестве натуральных чисел и принимающие значения того же множества.
Рекурсивный алгоритм – это алгоритм, решающий задачу путем решения одного или нескольких более узких вариантов той же задачи.
Рекурсивные функции - такие функции, которые могут вызывать сами себя. При этом каждый раз под каждый вызов создается совершенно новый набор локальных переменных, отличный от набора вызывающей функции.