Слайд 2
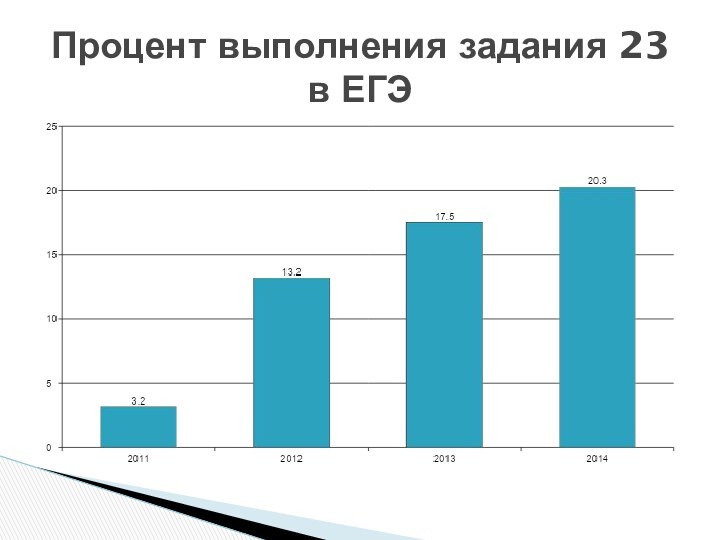
Процент выполнения задания 23 в ЕГЭ
Слайд 3
№1
Сколько различных решений имеет система уравнений
((X1
X2) (X3 X4)) (¬(X1 X2)
¬(X3 X4)) = 0
((X3 X4) (X5 X6)) (¬(X3 X4) ¬(X5 X6)) = 0
((X5 X6) (X7 X8)) (¬(X5 X6) ¬(X7 X8)) = 0
((X7 X8) (X9 X10)) (¬(X7 X8) ¬(X9 X10)) = 0
где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Слайд 4
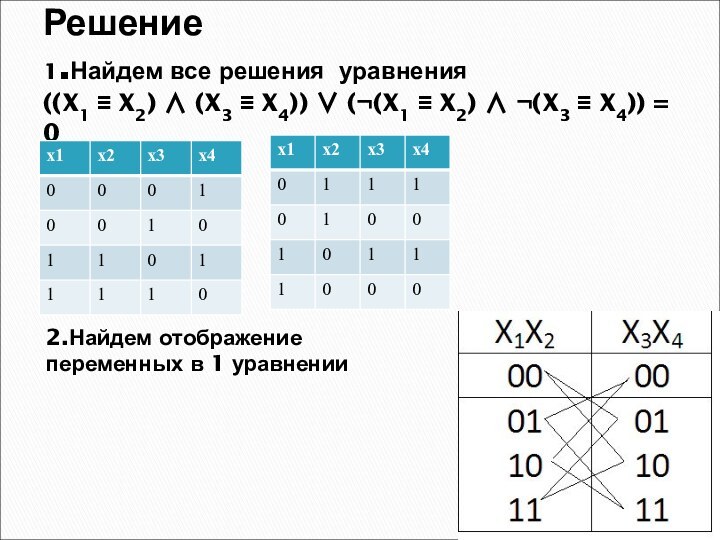
Решение
1.Найдем все решения уравнения
((X1 X2) (X3
X4)) (¬(X1 X2) ¬(X3
X4)) = 0
2.Найдем отображение переменных в 1 уравнении
Слайд 5
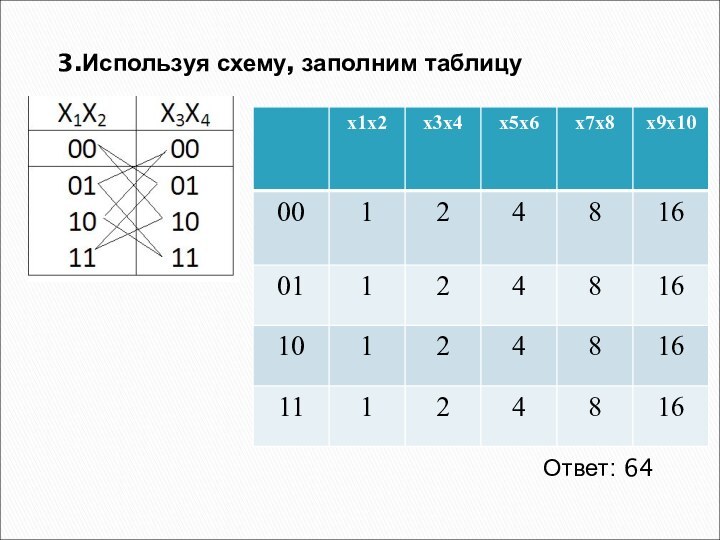
3.Используя схему, заполним таблицу
Ответ: 64
Слайд 6
№ 2
Сколько различных решений имеет система уравнений
(X1
X2) (¬X1 ¬X2) (X1
X3) = 1
(X2 X3) (¬X2 ¬X3) (X2 X4) = 1
...
(X7 X8) (¬X7 ¬X8) (X7 X9) = 1
(X8 X9) (¬X8 ¬X9) (X8 X10) = 0
где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Слайд 7
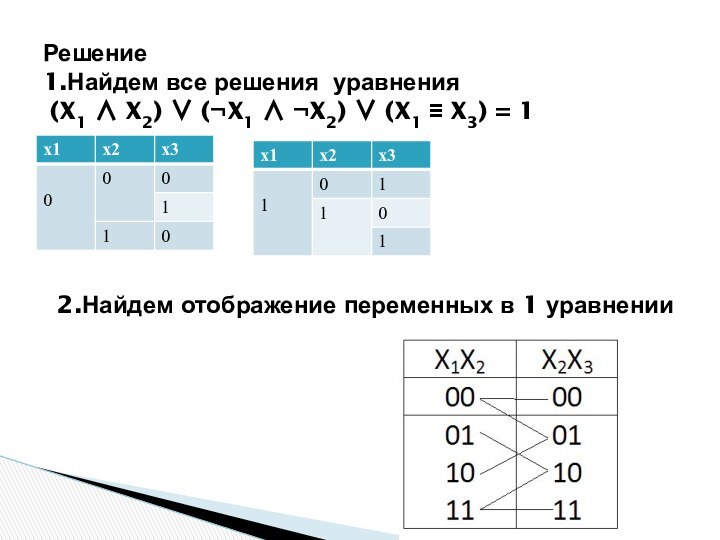
Решение
1.Найдем все решения уравнения
(X1 X2)
(¬X1 ¬X2) (X1 X3) = 1
2.Найдем
отображение переменных в 1 уравнении
Слайд 8
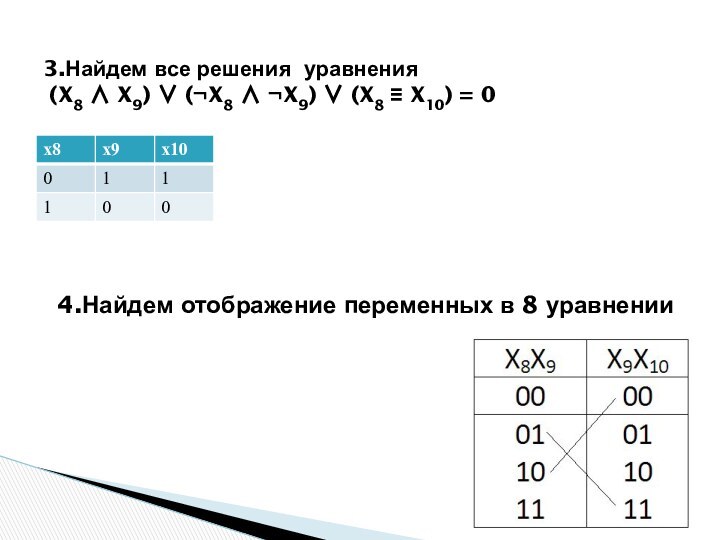
3.Найдем все решения уравнения
(X8 X9)
(¬X8 ¬X9) (X8 X10) = 0
4.Найдем
отображение переменных в 8 уравнении
Слайд 9
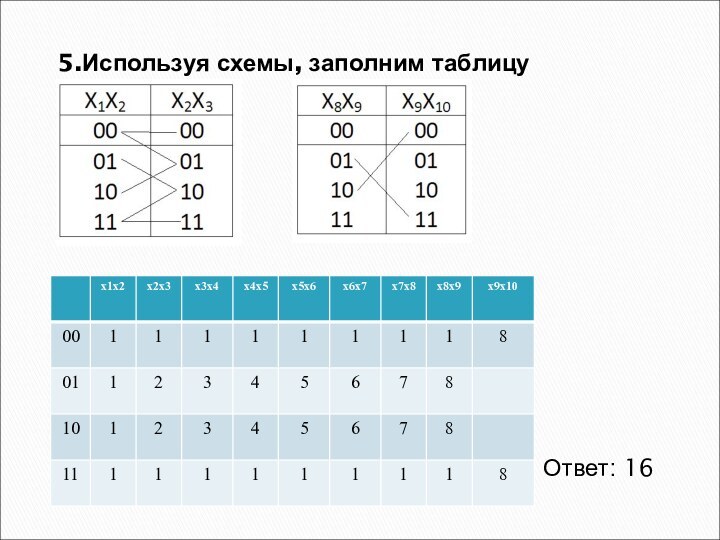
5.Используя схемы, заполним таблицу
Ответ: 16
Слайд 10
№ 3
Сколько различных решений имеет система уравнений?
(x1
x2)(x2 x3)(x3 x4)(x4 x5) =
1
(у1 у2)(у2 у3)(у3 у4)(у4 у5)= 1
x1 у1 = 0
где x1,x2,…,x5, у1,у2,…,у5 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Слайд 11
Решение
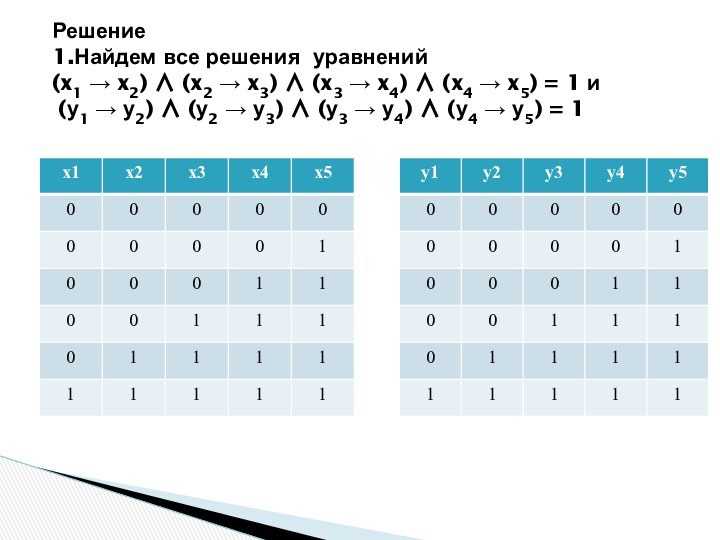
1.Найдем все решения уравнения
(x1 x2)(x2 x3)(x3
x4)(x4x5)=1,
учитывая x1 у1 = 0 (x1
= 0 , у1 = 0 )
Слайд 12
2.Найдем все решения уравнения
(у1 у2)(у2 у3)(у3
у4)(у4 у5)= 1
учитывая x1 у1 =
0 (x1 = 0 , у1 = 0 )
Слайд 13
3. Уравнения
(x1 x2)(x2 x3)(x3 x4)(x4
x5) = 1,
(у1 у2)(у2 у3)(у3
у4)(у4 у5)= 1
независимые.
Условие x1 у1 = 0 выполняется для всех найденных решений
Поэтому, система имеет
5∙5=25 различных решений.
Ответ: 25
Слайд 14
№ 4
Сколько различных решений имеет система уравнений?
(x1
x2) (x2 x3) (x3
x4) (x4 x5) = 1
(у1 у2) (у2 у3) (у3 у4) (у4 у5) = 1
(x1 y1) (x2 y2) (x3 y3) = 1
где x1,x2,…,x5, у1,у2,…,у5 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Слайд 15
Решение
1.Найдем все решения уравнений
(x1 x2) (x2
x3) (x3 x4) (x4
x5) = 1 и
(у1 у2) (у2 у3) (у3 у4) (у4 у5) = 1
Слайд 16
Уравнения
(x1 x2) (x2 x3)
(x3 x4) (x4 x5) = 1
(у1
у2) (у2 у3) (у3 у4) (у4 у5) = 1
независимые.
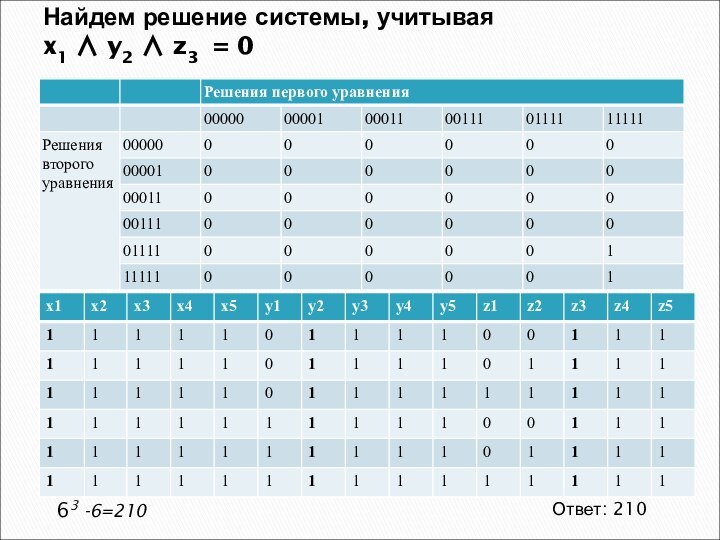
Найдем решение системы, учитывая
(x1 y1) (x2 y2) (x3 y3) = 1
Ответ: 24
Слайд 17
№ 5
Сколько различных решений имеет система уравнений?
x1
x2 x3 x4 x5 =
1
y1 y2 y3 y4 y5 = 0
где x1,x2,…,x5, у1,у2,…,у5 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Слайд 18
количество решений уравнения с нулём в правой части,
обозначим через ZN, где N – количество переменных; количество
решений уравнения с единицей в правой части, обозначим через KN.
Очевидно, что ZN +KN =2N ZN =KN-1
ZN = KN-1 = 2N-1 –ZN-1
y1 y2= 0 , Z2 =1
y1 y2 y3 = 0 , Z3 = 23-1 –Z3-1 =4-1=3
y1 y2 y3 y4 = 0, Z4 = 24-1 –Z4-1 =8-3=5
y1 y2 y3 y4 y5 = 0, Z5 = 25-1 –Z5-1 =16-5=11
Уравнение имеет 11 решений
Решение
1.Найдем количество решений уравнения
y1 y2 y3 y4 y5 = 0
Слайд 19
2.Найдем количество решений уравнения
x1 x2 x3
x4 x5 = 1
ZN +KN =2N
KN
=2N -ZN = 25 –Z5 = 32-11=21
3. Уравнения
x1 x2 x3 x4 x5 = 1
y1 y2 y3 y4 y5 = 0
независимые.
Поэтому, система имеет
21∙11=231 различных решений.
Ответ: 231
Слайд 20
№ 6
Сколько различных решений имеет система логических
уравнений
(x1 x2) (x2 x3)
(x3 x4) (x4 x5) = 1
(y1 y2) (y2 y3) (y3 y4) (y4 y5) = 1
(z1 z2) (z2 z3) (z3 z4) (z4 z5) = 1
x1 y2 z3 = 0
где x1, …, x5, y1, …, y5, z1, …, z5, – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов
Слайд 21
Решение
Уравнения
(x1 x2) (x2 x3)
(x3 x4) (x4 x5) = 1
(y1
y2) (y2 y3) (y3 y4) (y4 y5) = 1
(z1 z2) (z2 z3) (z3 z4) (z4 z5) = 1
независимые.
Каждое из уравнений имеет 6 различных решений:
00000, 00001, 00011, 00111, 01111, 11111.
Слайд 22
Найдем решение системы, учитывая
x1 y2
z3 = 0
Ответ: 210
63 -6=210
Слайд 23
№ 7
Сколько различных решений имеет система логических уравнений
(x1 V x2) ((x1 x2) x3)
¬(x1 y1 )= 1
(x2 V x3) ((x2 x3) x4) ¬(x2 y2 )= 1
…
(x5 V x6) ((x5 x6) x7) ¬(x5 y5 )= 1
(x6 V x7) ¬(x6 y6 )= 1
x7 y7=0
где x1, …, x5, y1, …, y5, z1, …, z5, – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов
Слайд 24
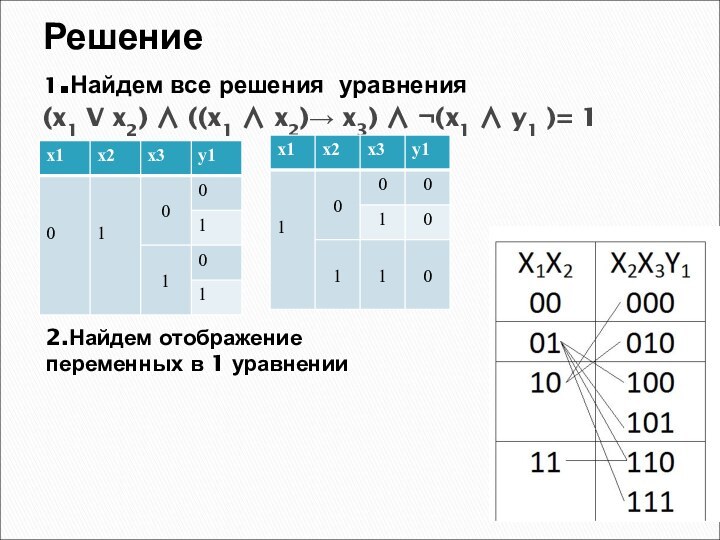
Решение
1.Найдем все решения уравнения
(x1 V x2) ((x1
x2) x3) ¬(x1 y1 )= 1
2.Найдем
отображение переменных в 1 уравнении
Слайд 25
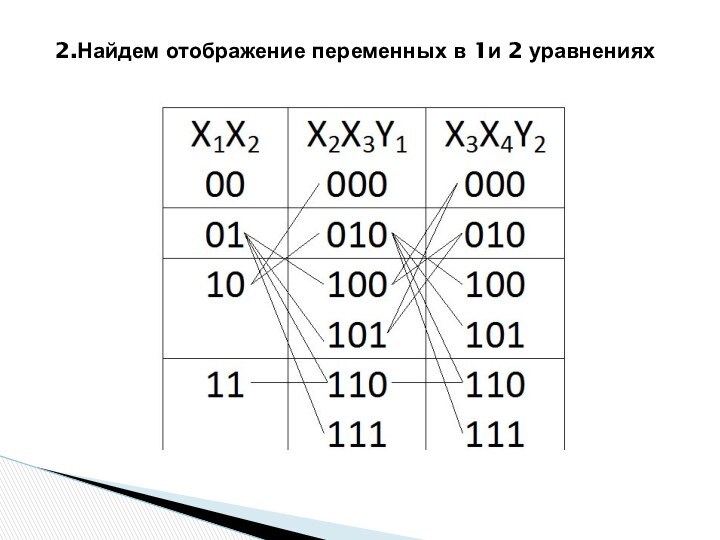
2.Найдем отображение переменных в 1и 2 уравнениях
Слайд 26
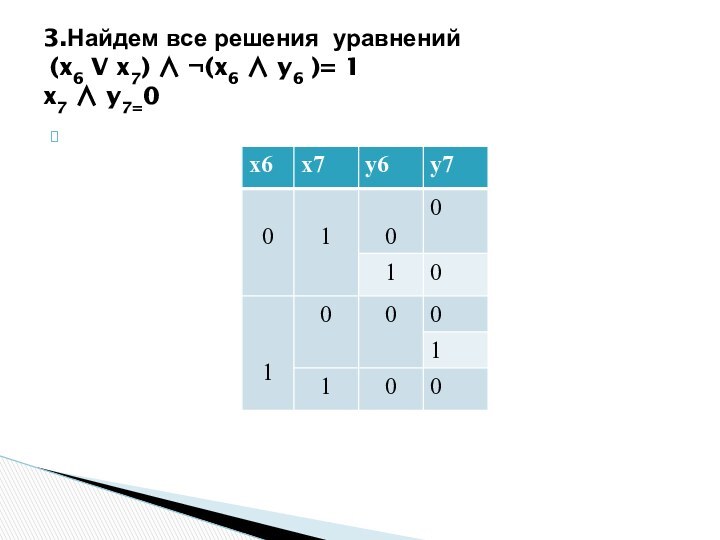
3.Найдем все решения уравнений
(x6 V x7)
¬(x6 y6 )= 1
x7 y7=0
Слайд 27
4.Найдем отображение переменных в уравнениях
Слайд 28
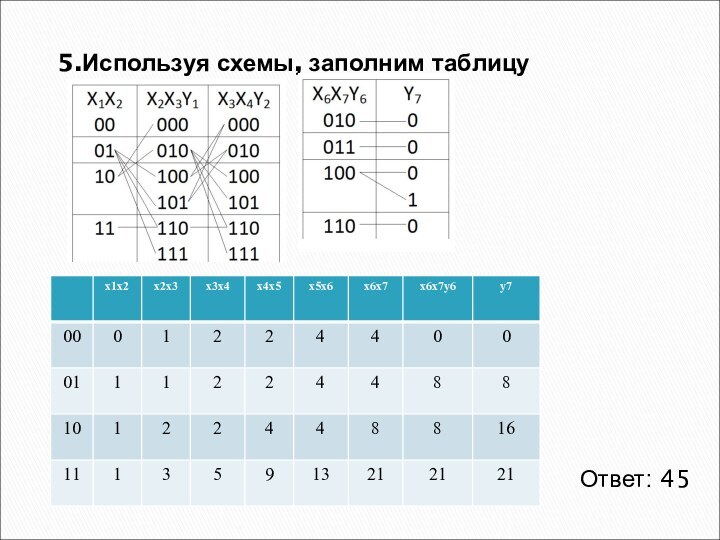
5.Используя схемы, заполним таблицу
Ответ: 45