числовой информации
Перевод чисел из одной систем счисления в
другую Содержание:
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть















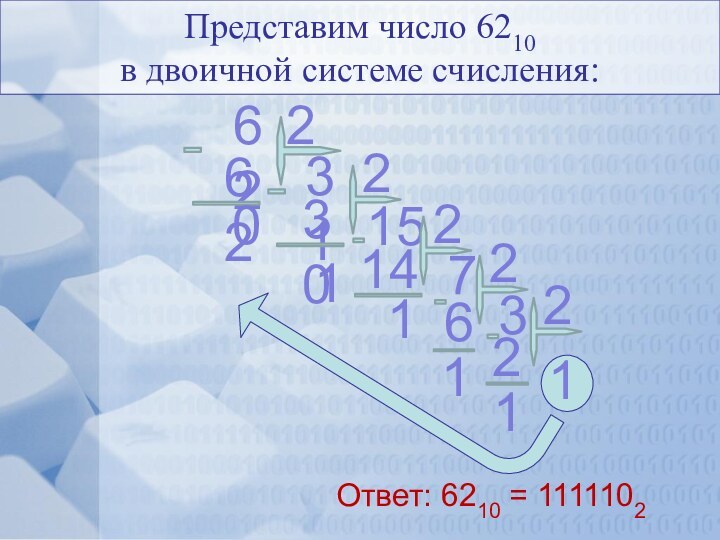
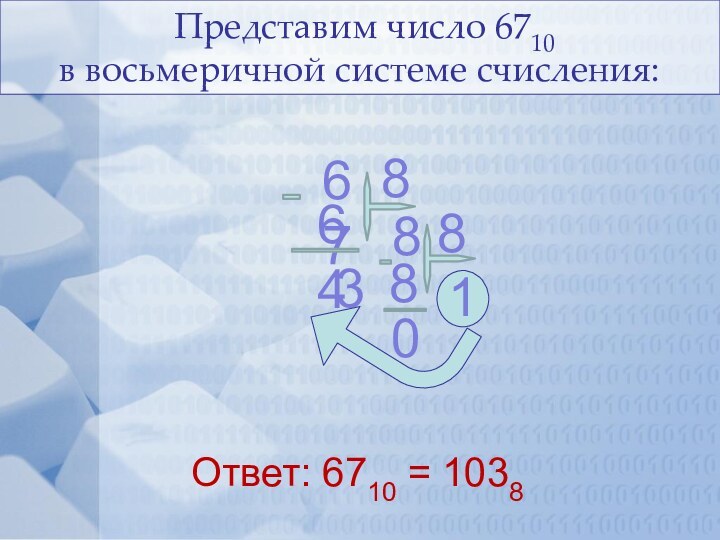


Содержание:
А что такое система счисления?
Система счисления
непозиционная
позиционная
Унарная – одна цифра обозначает единицу (1 день,
1 камень, 1 баран, …)
Более совершенные непозиционные с/с.
К их числу относились славянская, греческая, финикийская и др. В них числа от 1 до 9, целые количества десятков (от 10 до 90) и целые количества сотен (от 10 до 900) обозначались буквами алфавита.
В России славянская нумерация сохранилась до конца 17 века. При Петре I возобладала арабская нумерация, которой пользуемся до сих пор.
Греки над буквами, обозначающими числа, ставили специальный знак – титло.
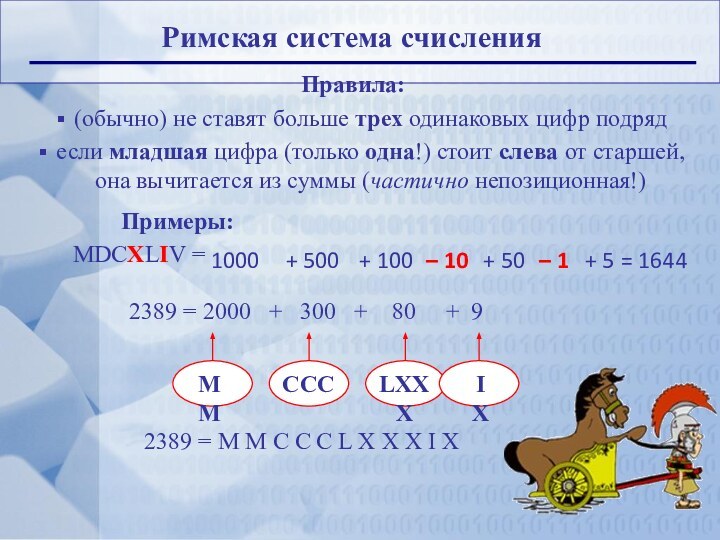
1000
+ 500
+ 100
– 10
+ 50
– 1
+ 5
2389 = 2000 + 300 + 80 + 9
2389 = M M C C C L X X X I X
M M
CCC
LXXX
IX
= 1644
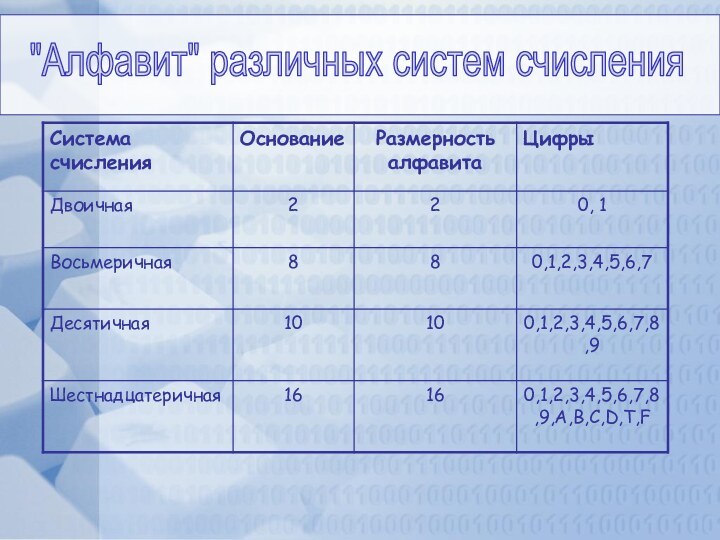
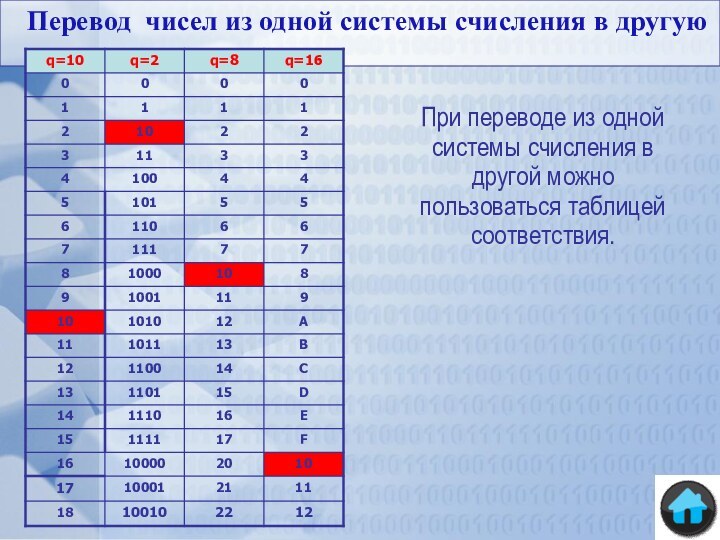
Основание позиционной системы счисления - это количество различных символов, используемых для изображения чисел в данной системе счисления.
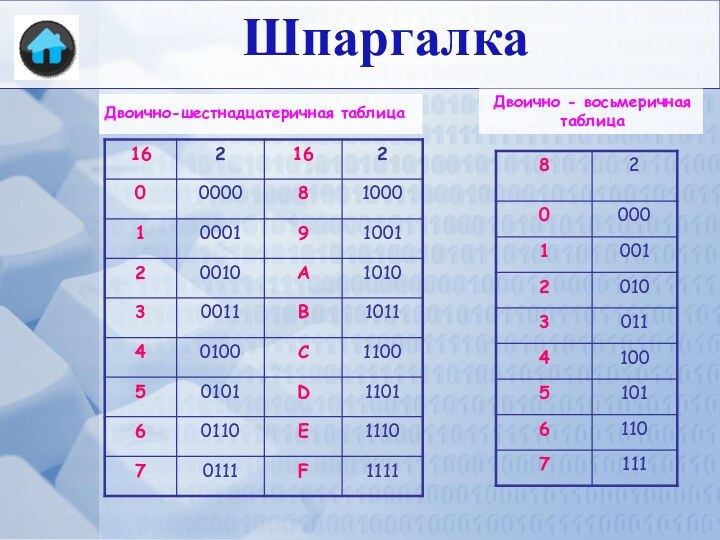
В настоящее время, кроме хорошо известной нам десятичной системы счисления, в вычислительной технике используются двоичная, восьмеричная, и шестнадцатеричная системы счисления. Все применяемые в настоящее время системы счисления позиционные.
234
Две сотни
Три десятка
Четыре единицы
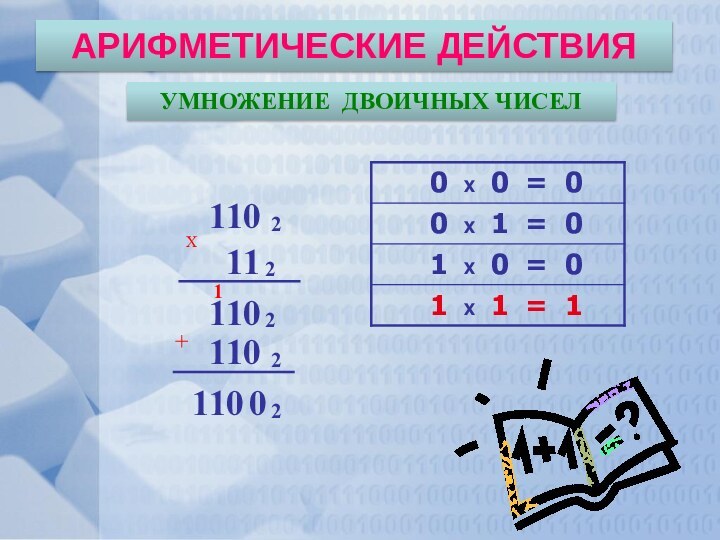
АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ
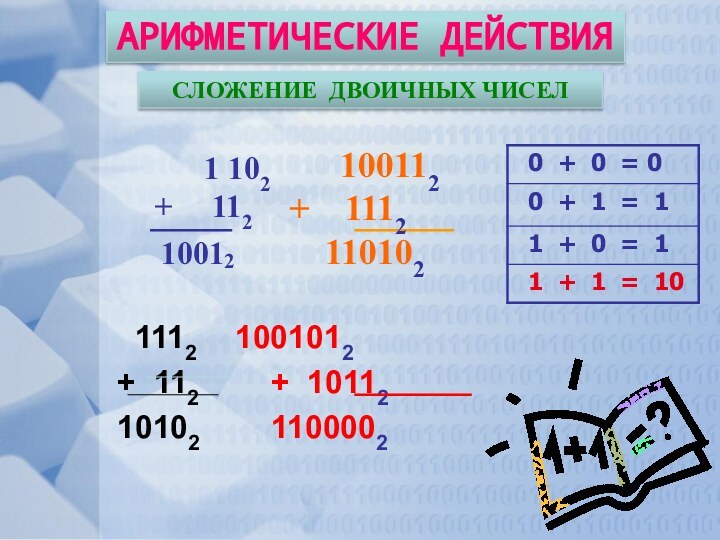
СЛОЖЕНИЕ ДВОИЧНЫХ ЧИСЕЛ
АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ
100112
+ 1112
110102
1 102
+ 112
2
1001
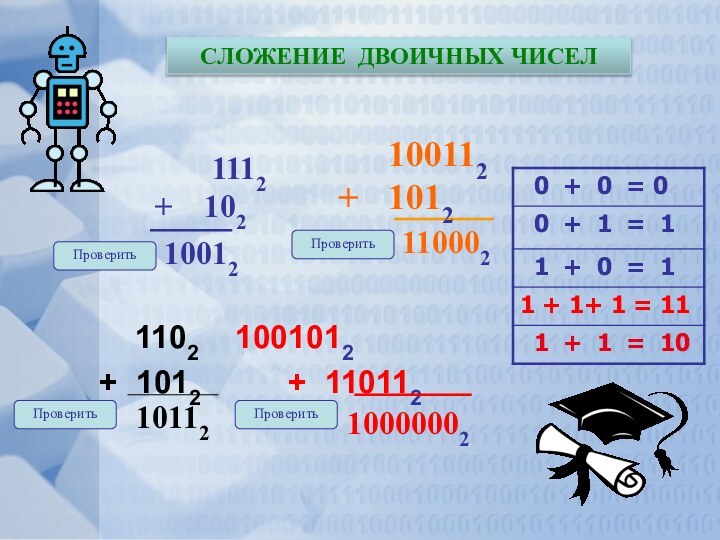
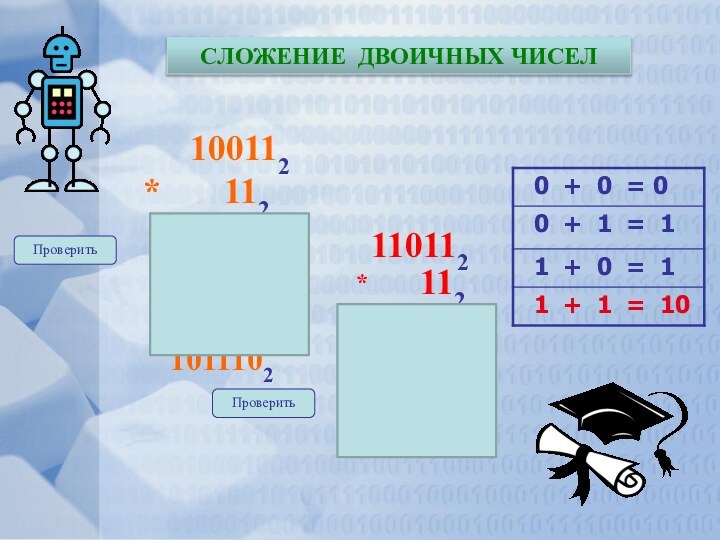
СЛОЖЕНИЕ ДВОИЧНЫХ ЧИСЕЛ
100112
+ 1012
1112
+ 102
10012
Проверить
Проверить
Проверить
Проверить
110002
10112
10000002
Проверить
Проверить
100112
1011102
100112
+
110112
110112
110112
112
101102
*
+
10112 =
1*23+
0*22+
1*21+
1*20=
1*8+
0*4+
1*2+
1*1=
1110
3 2 1 0
Разложение чисел
по степеням основания
6758=
?
Проверить
6*82+7*81+5*80= 6*64+7*8+5*1=44510
1А16=
?
Проверить
1*161+10*160=16+10=2610