of array – a sequence of one or more
consecutive elements in array.D-good segment – segment, in which sum of elements not greater than D.
Count the pairs (L, R) such that segment [L, R] of array A is D-good.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть



![Two pointers method 2. Primitive solutionNotice that sum(L, R) = sum(L, R-1)+A[R]If sum(L, R1)>D then](/img/tmb/15/1459735/5dc10f0c11bc12b0a3522670226c281c-720x.jpg)

![Two pointers method 3. Good solutionprefixSum[0] = a[0];for (int i = 1; i < n;](/img/tmb/15/1459735/033580dbc1e6f8f43d1910ebd7672db7-720x.jpg)

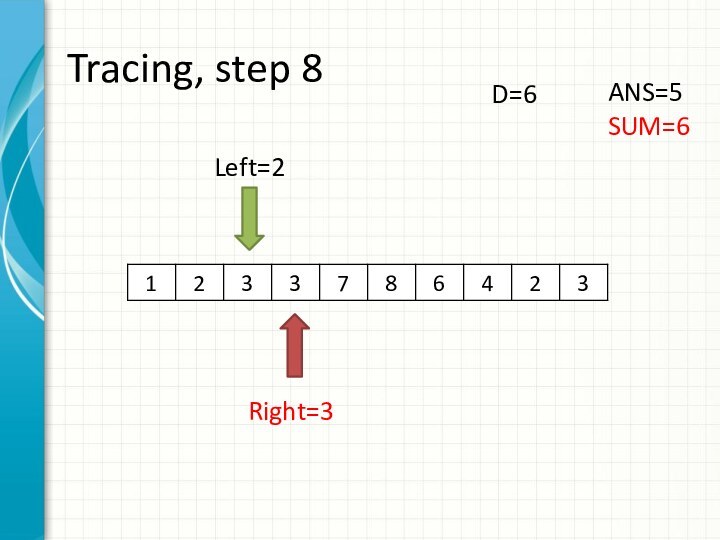
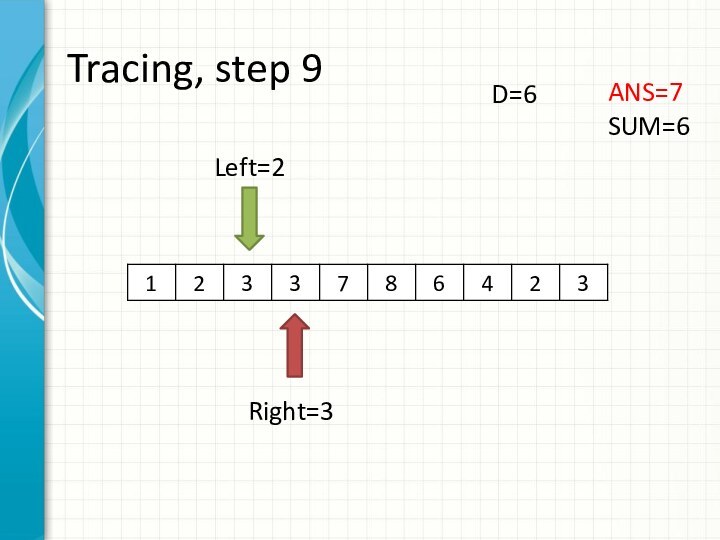
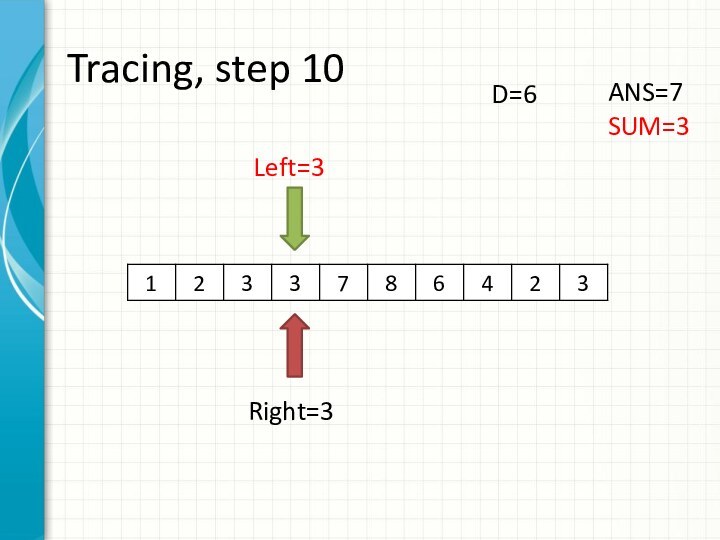
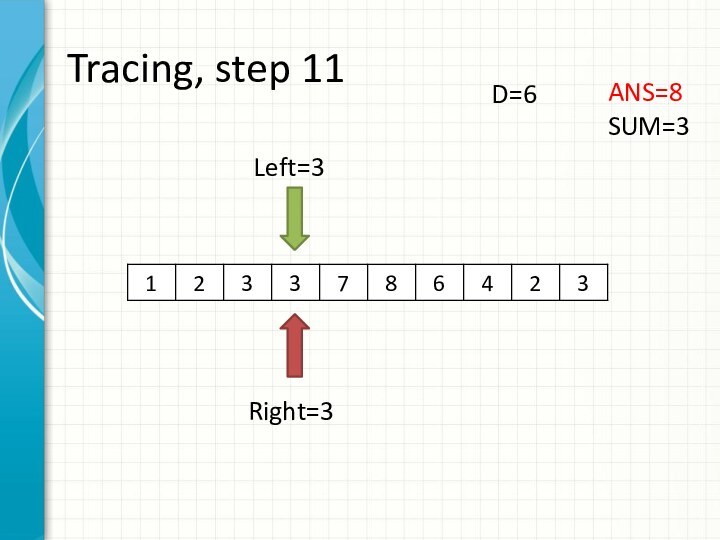


O(N3)
O(N2)
O(NlogN)
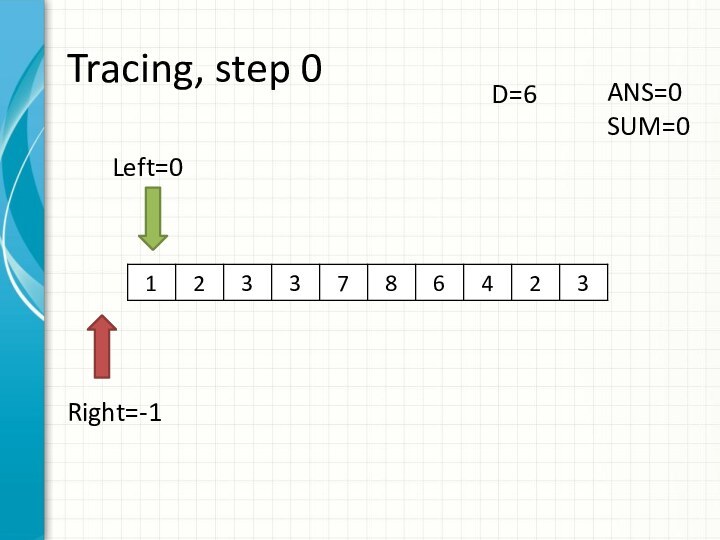
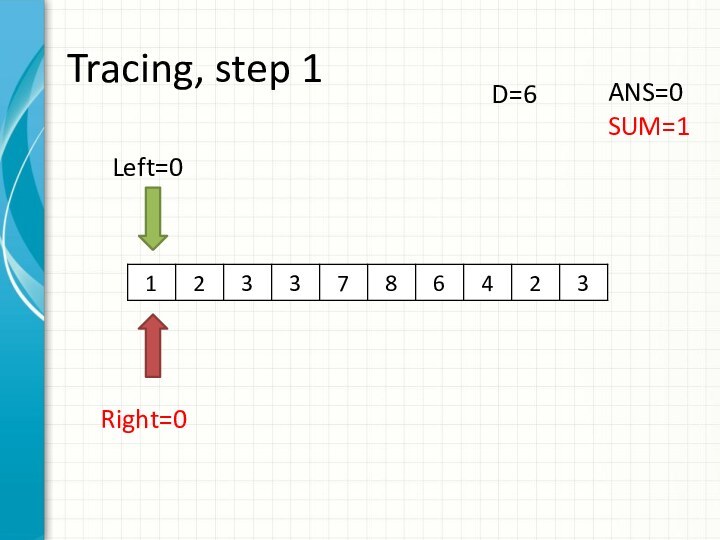
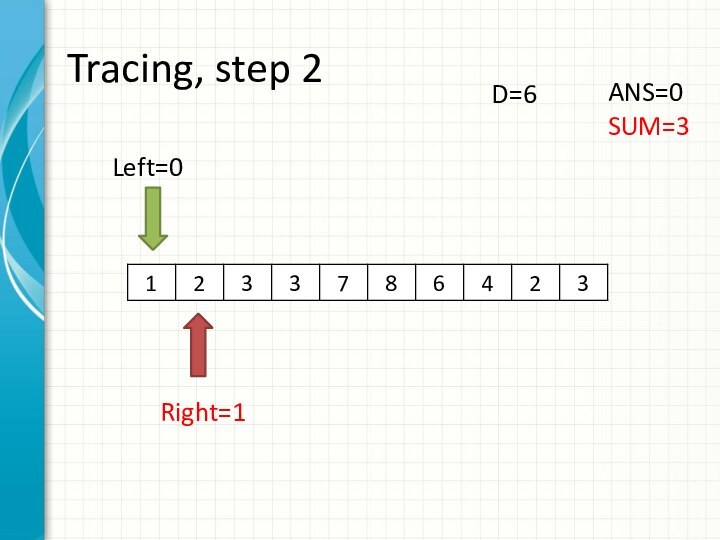
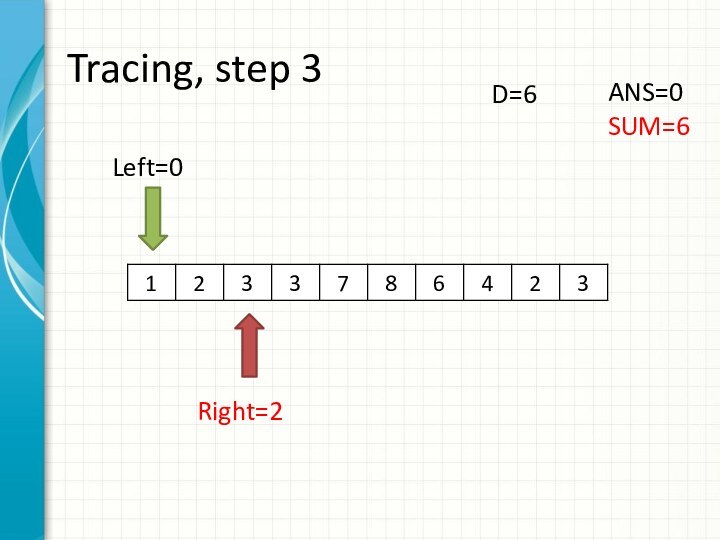
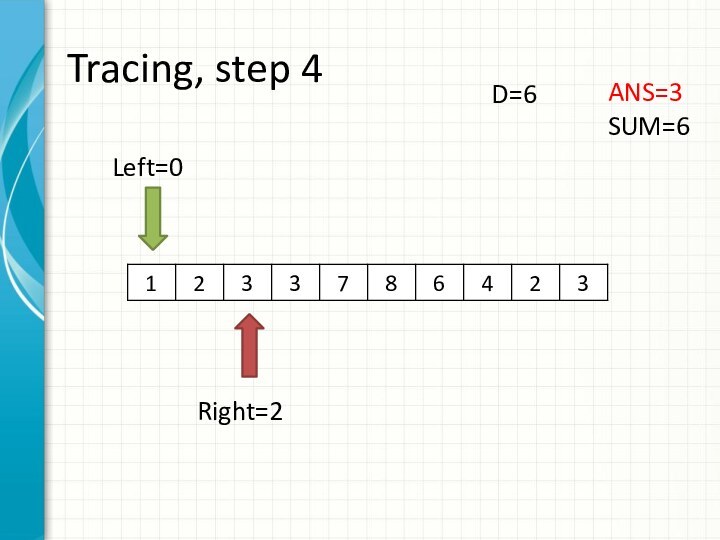
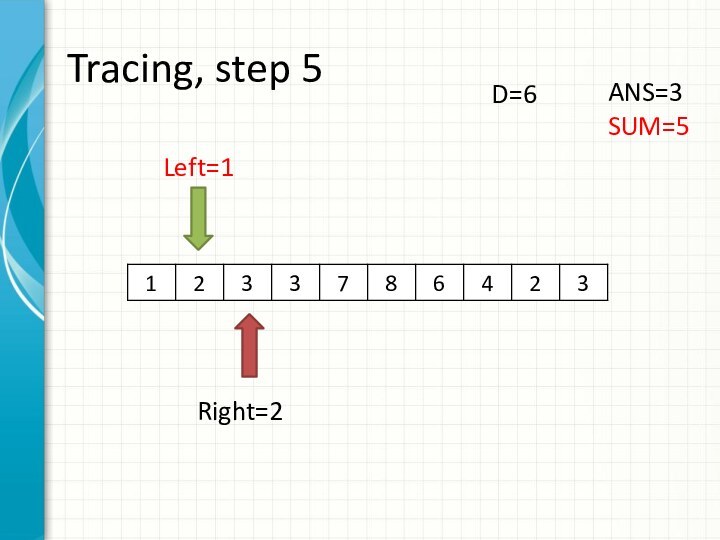
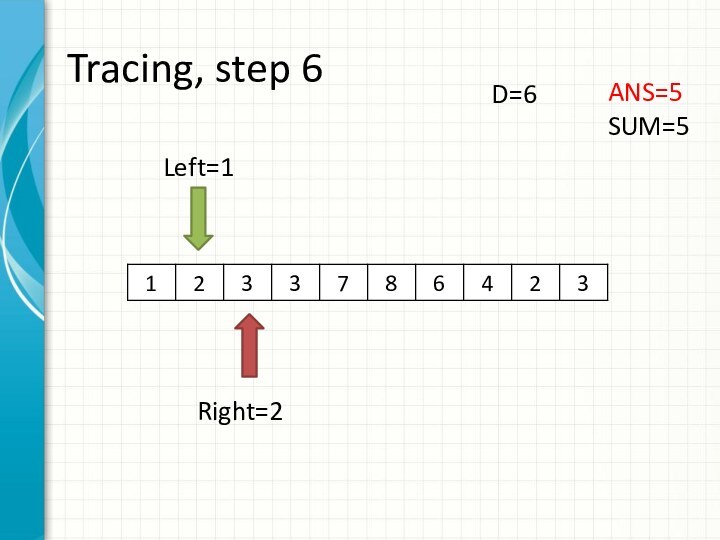
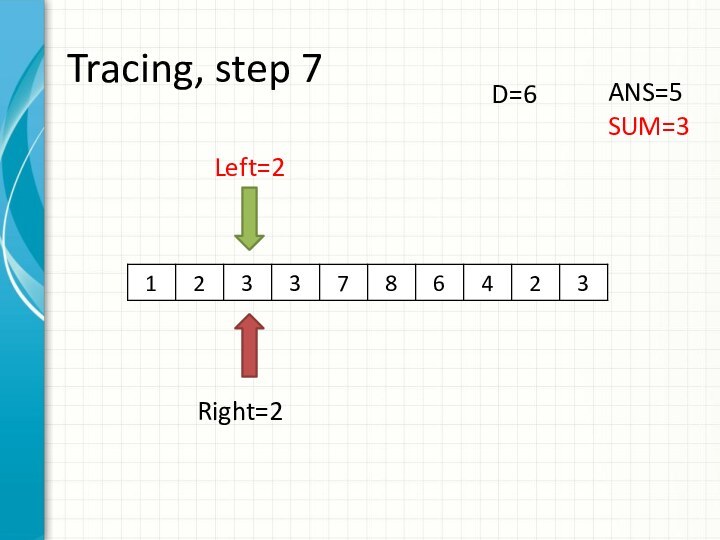
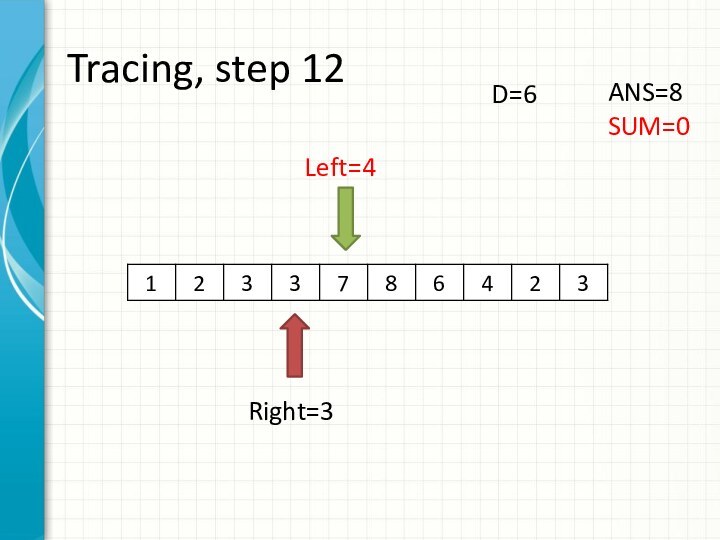
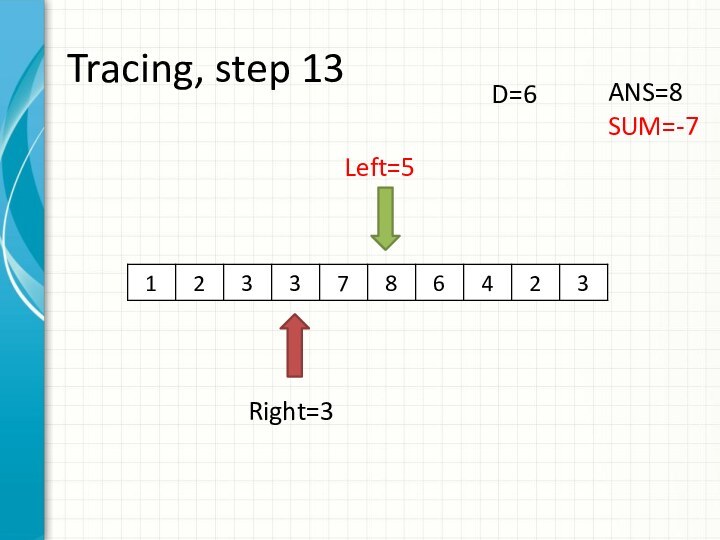
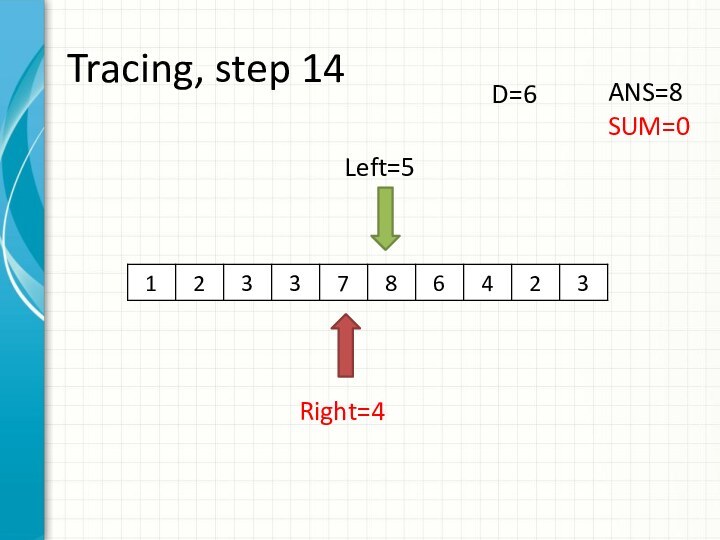
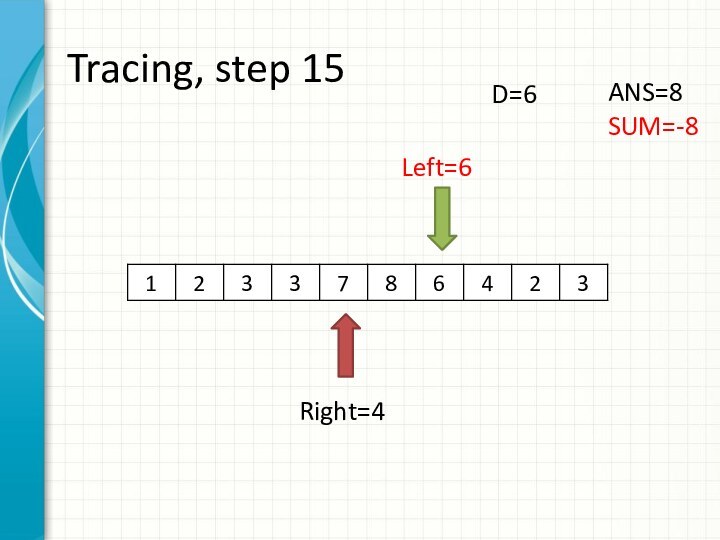
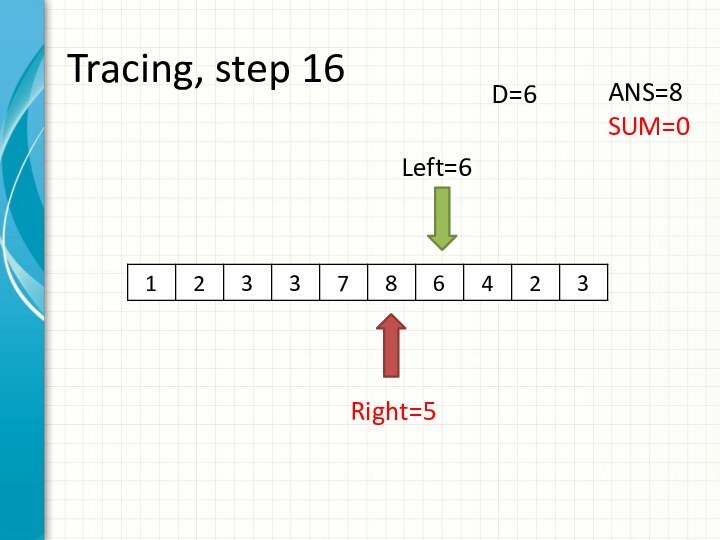
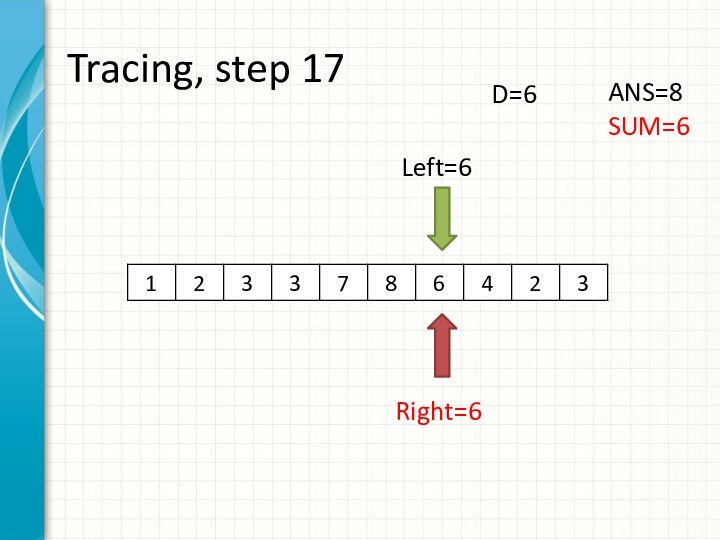
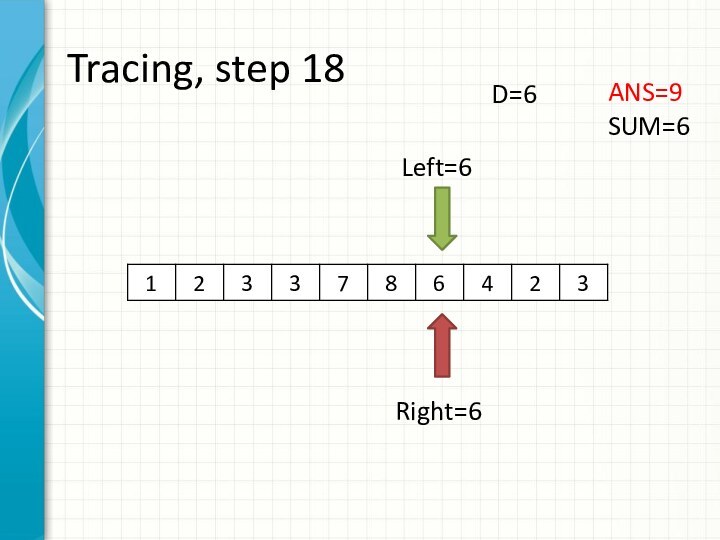
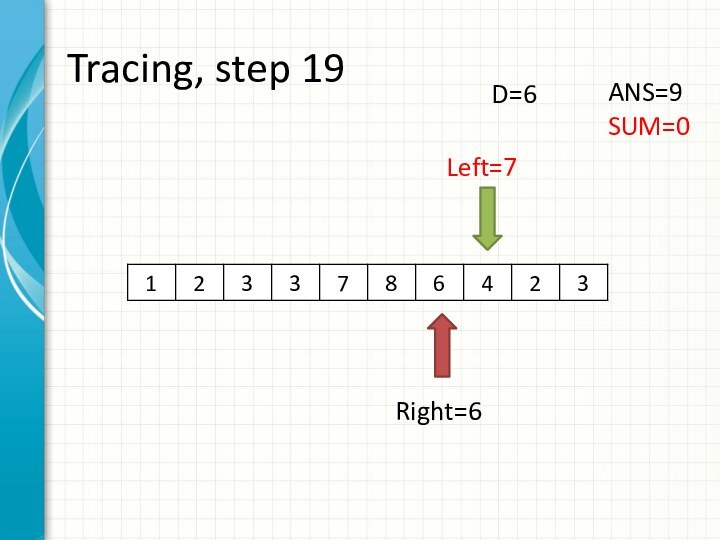
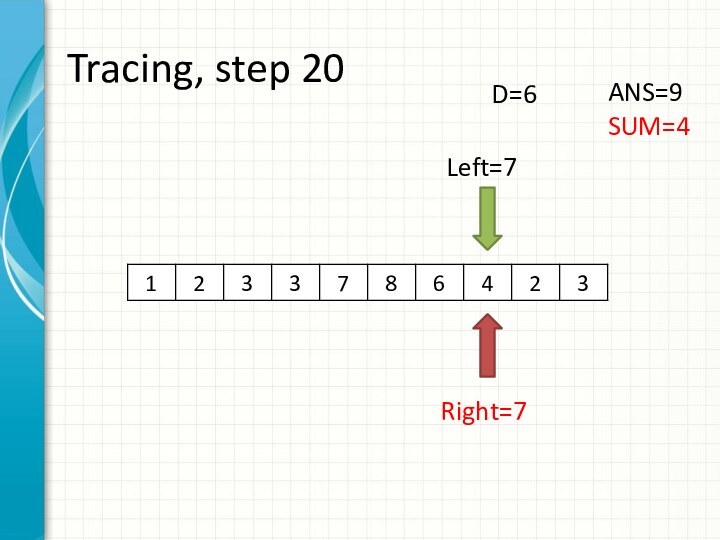
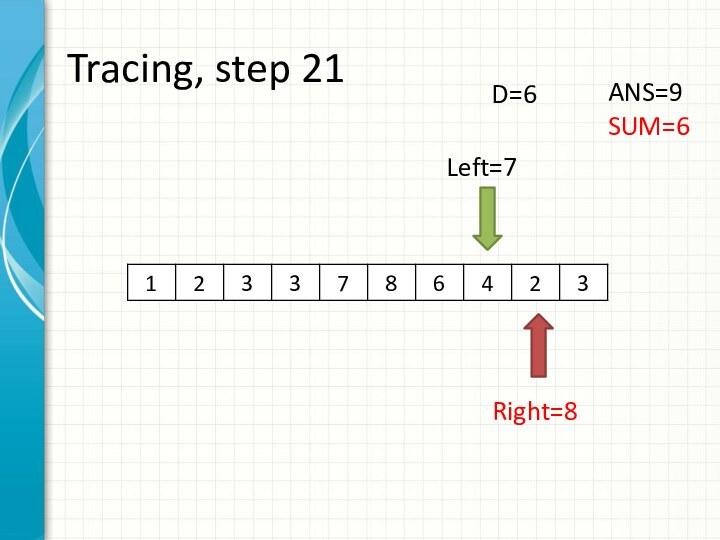
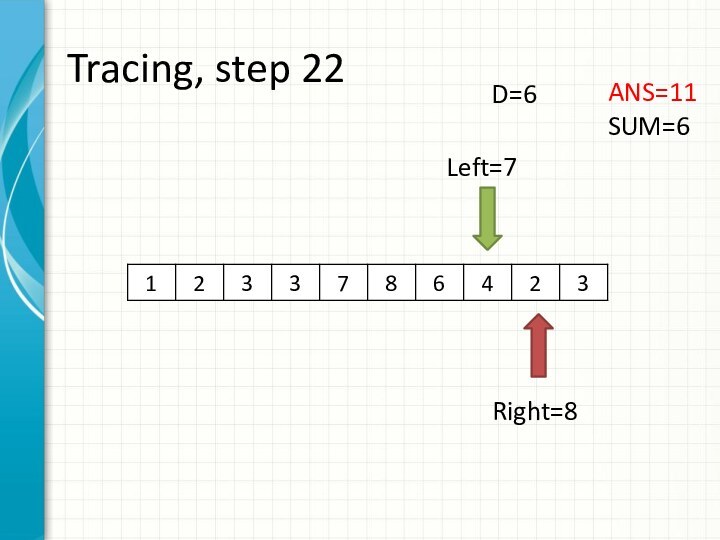
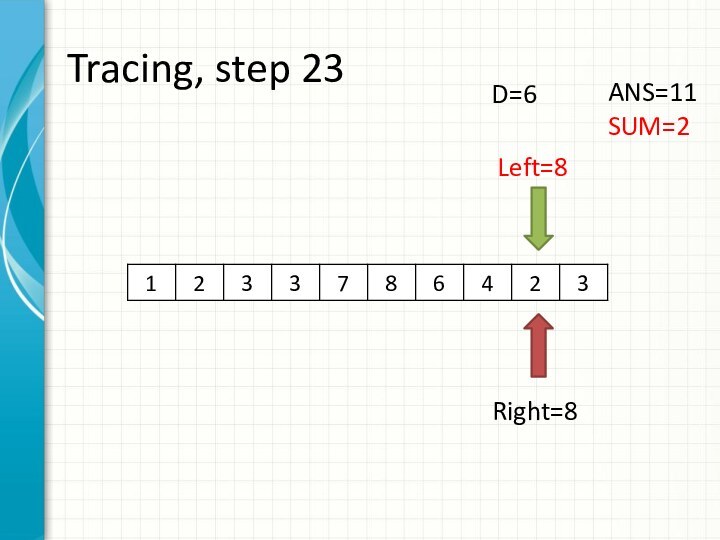
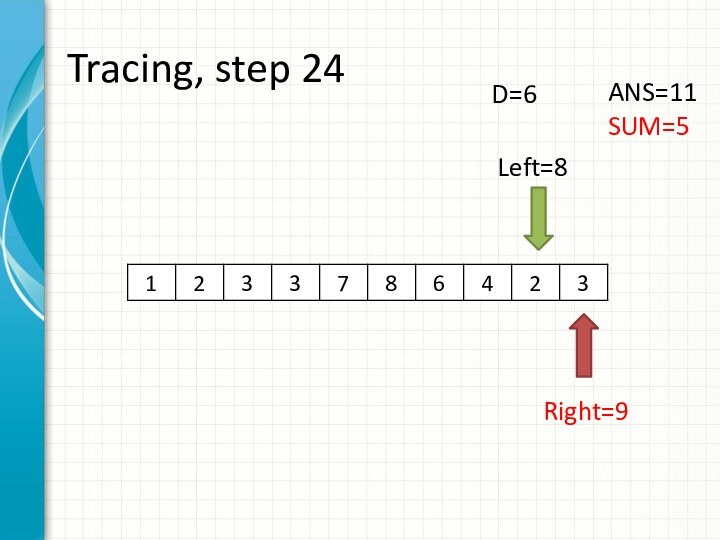
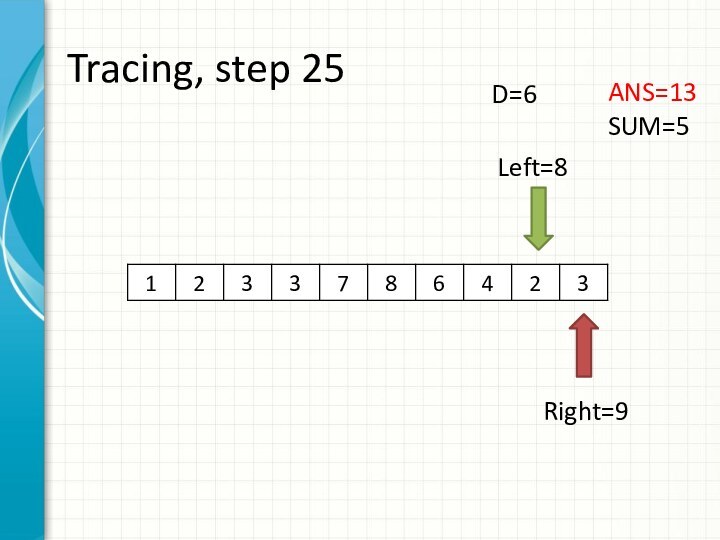
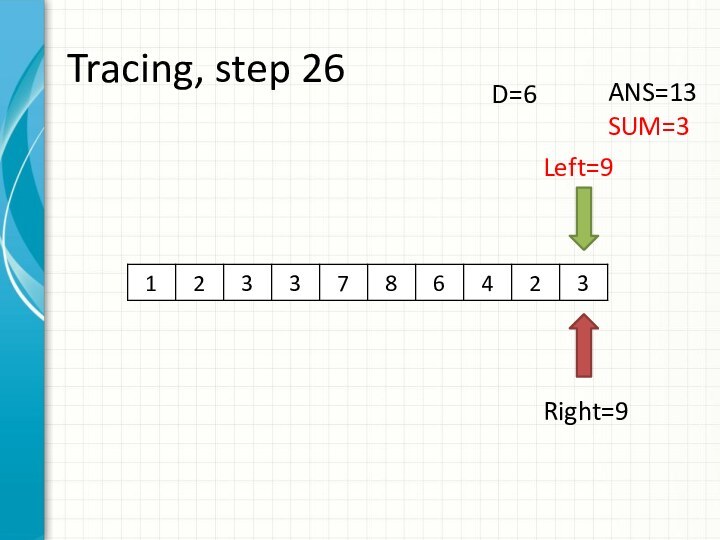
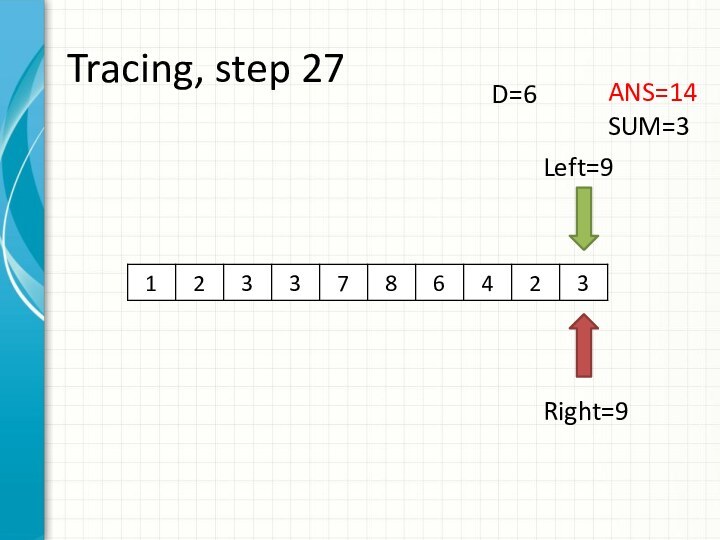
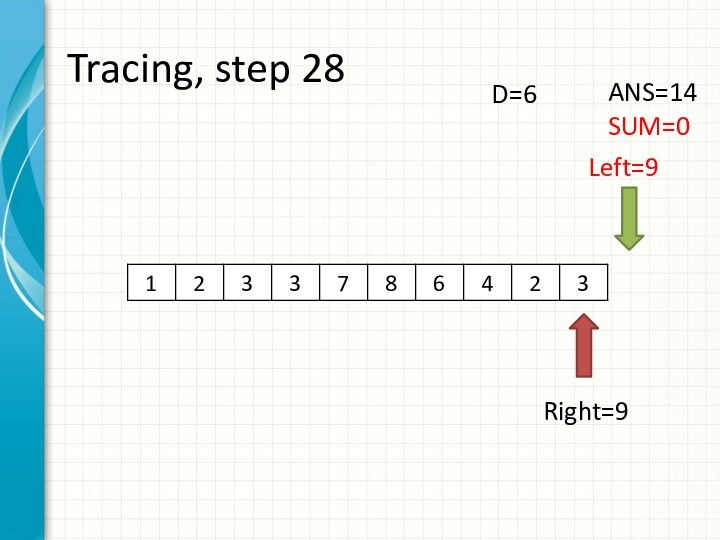
int right = -1;
int sum = 0;
for (int i = 0; i < n; ++i)
{
while (right + 1 < n && sum + a[right + 1] <= d)
sum += a[++right];
ans += right - i + 1;
sum -= a[i];
}
O(N)