предназначенная для эффективного обслуживания случайного потока заявок (требований на
обслуживание) при ограничениях на ресурсы системы. "Моделирование", 2013,
вопрос 17
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть











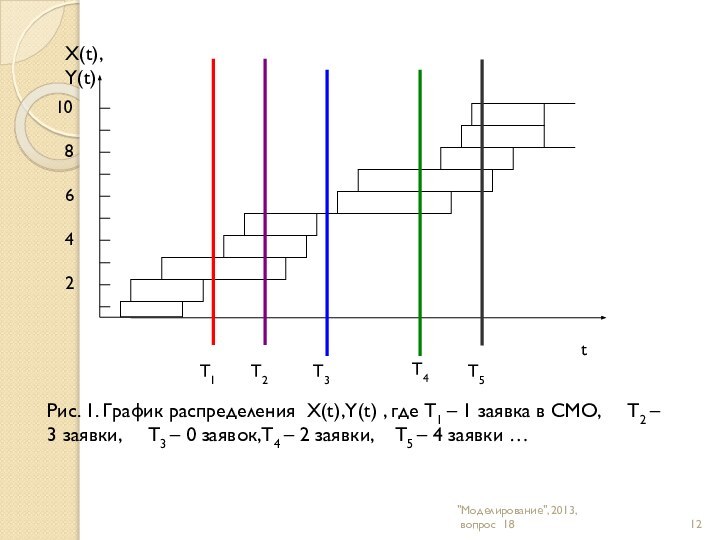





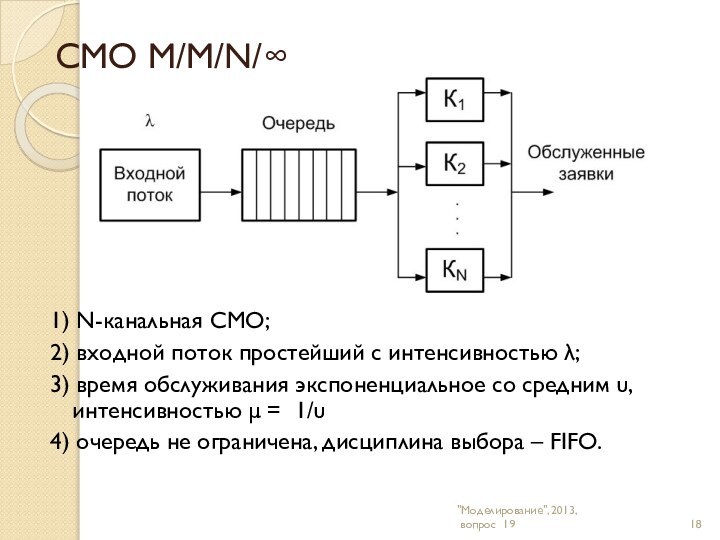

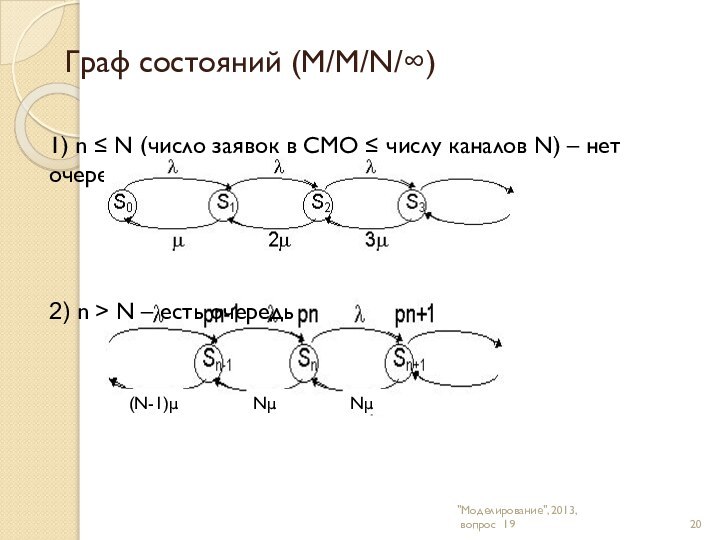







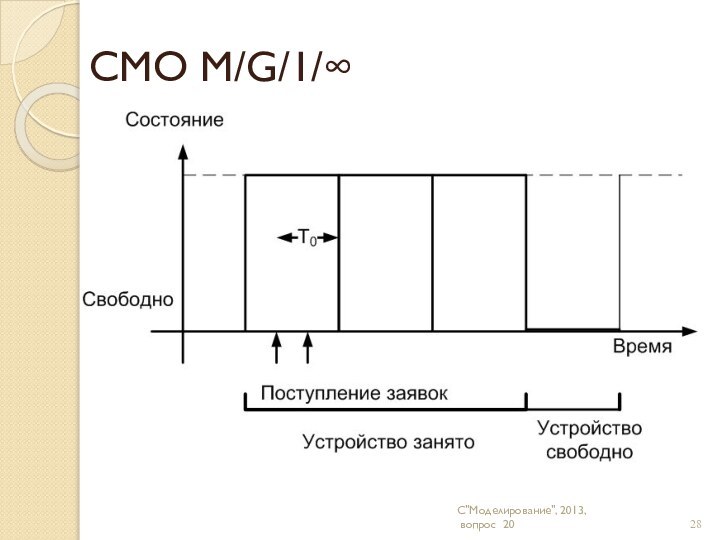








































"Моделирование", 2013,
вопрос 17
w - время ожидания заявки в очереди на обслуживание
среднее время обслуживания
"Моделирование", 2013,
вопрос 17
"Моделирование", 2013,
вопрос 17
"Моделирование", 2013,
вопрос 18
"Моделирование", 2013,
вопрос 18
"Моделирование", 2013,
вопрос 18
"Моделирование", 2013,
вопрос 18
"Моделирование", 2013,
вопрос 18
"Моделирование", 2013,
вопрос 19
"Моделирование", 2013,
вопрос 19
С"Моделирование", 2013,
вопрос 20
С"Моделирование", 2013,
вопрос 20
С"Моделирование", 2013,
вопрос 20
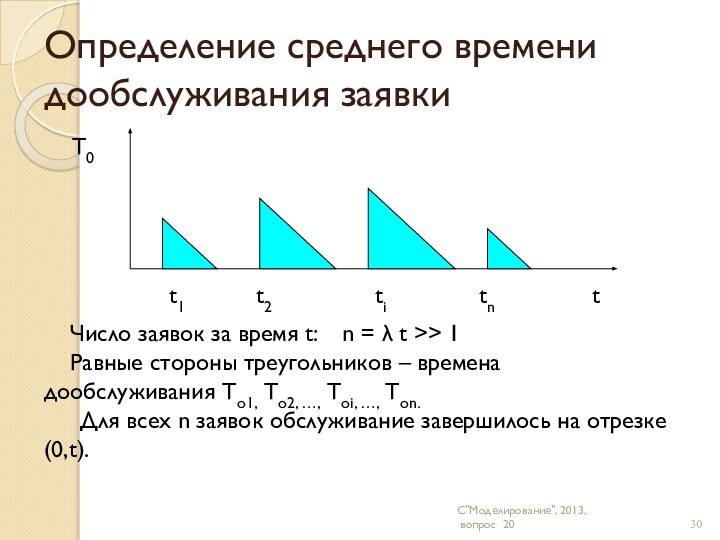
где u – ср. время пребывания заявки в системе
Для экспоненциального распределения (2) = 2 2
подставим в формулу (3) и получим:
С"Моделирование", 2013,
вопрос 21
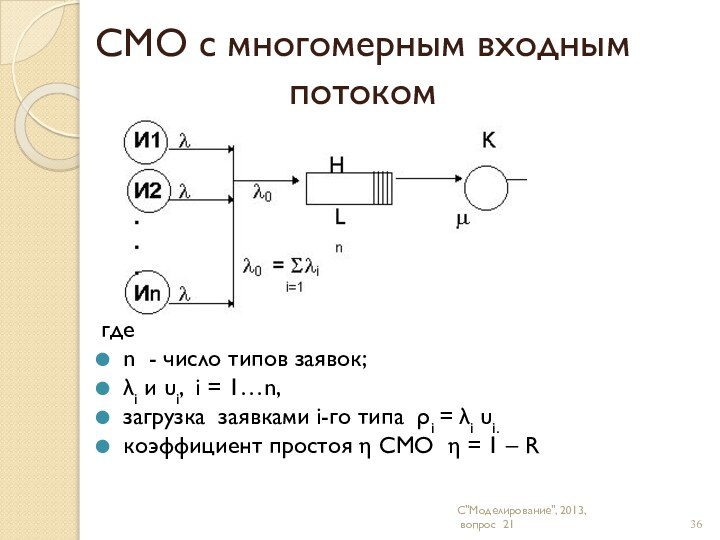
Ср. число заявок i-го типа в системе:
"Моделирование", 2013,
вопрос 21
"Моделирование", 2013,
вопрос 21
"Моделирование", 2013,
вопрос 21
"Моделирование", 2013,
вопрос 21
СевНТУ, кафедра КиВТ, курс "Моделирование", 2013, Лекция 5
"Моделирование", 2013,
вопрос 21
"Моделирование", 2013,
вопрос 22
"Моделирование", 2013,
вопрос 22
"Моделирование", 2013,
вопрос 22
"Моделирование", 2013,
вопрос 22
"Моделирование", 2013,
вопрос 22
"Моделирование", 2013,
вопрос 22
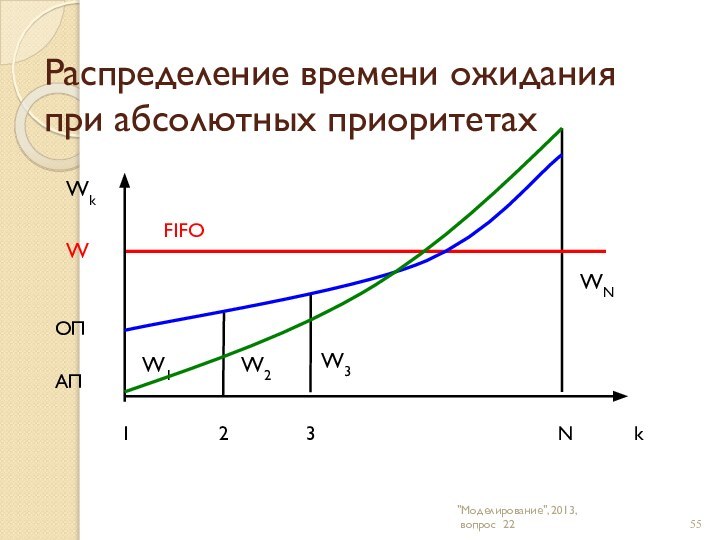
Закон сохранения времени ожидания
"Моделирование", 2013,
вопрос 22
Закон сохранения времени ожидания
"Моделирование", 2013,
вопрос 22
"Моделирование", 2013,
вопрос 23
"Моделирование", 2013,
вопрос 23
СевНТУ, кафедра КиВТ, курс "Моделирование", 2013, Лекция 6
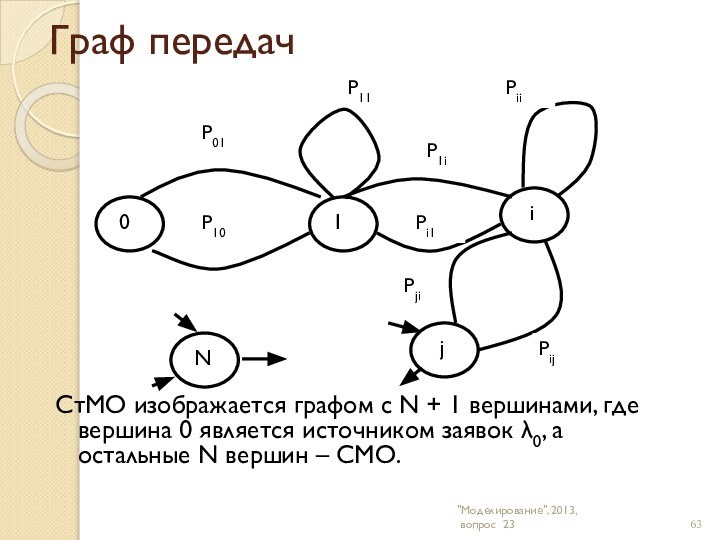
"Моделирование", 2013,
вопрос 23
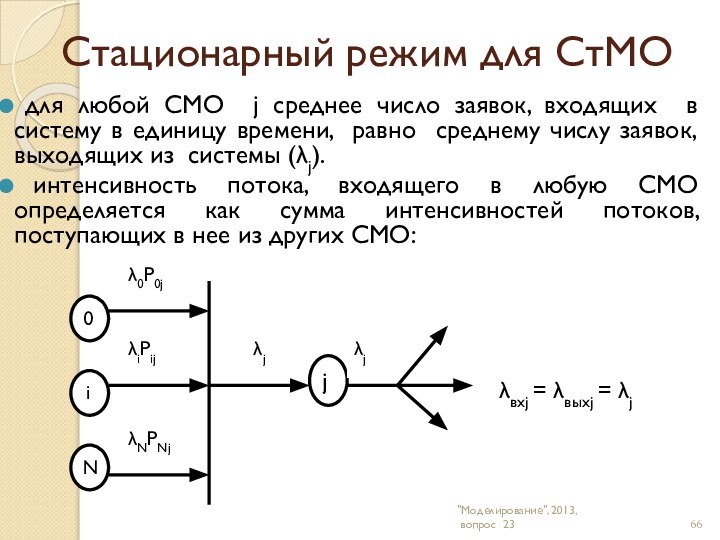
вхj = выхj = j
"Моделирование", 2013,
вопрос 23
"Моделирование", 2013,
вопрос 23
"Моделирование", 2013,
вопрос 23
"Моделирование", 2013,
вопрос 23
В стационарном режиме
7) Среднее время пребывания заявки в узле