данных и базовые конструкции языка Haskell
Элементарные типы данных
Integer,
Int – целые значения (25, -17, 111222333444555666777888) Float, Double – вещественные значения (3.14, -2.718281828459045)
Char – символьные значения ('A', '*', '3')
Bool – логические значения (True, False)
Идентификаторы: fact, fAcToRiAl, fact_1, fact''
Знаки операций: +, -, *, <, ==
Идентификаторы применяются для обозначения констант – значений разных типов (простых, составных, функций) и типов. Любому идентификатору можно сопоставить тип и значение:
school :: Integer
school = 366
piHalf :: Double
piHalf = 3.1415926536 / 2




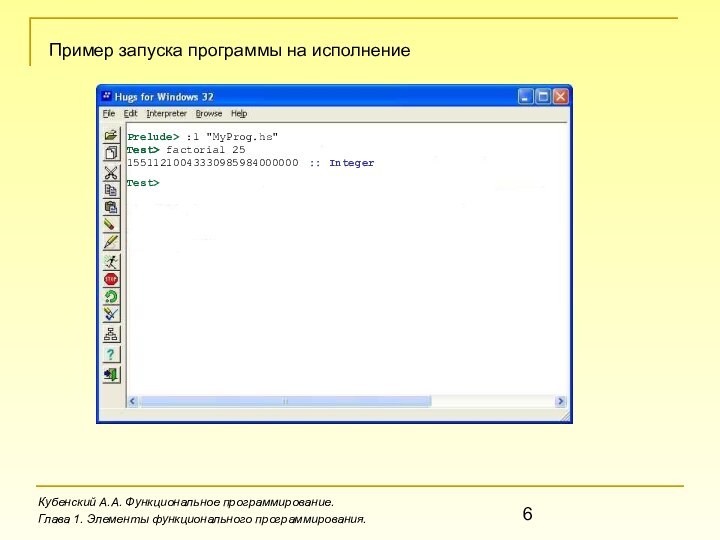 factorial 2515511210043330985984000000 :: IntegerTest> Test>Пример запуска программы на исполнениеКубенский">
factorial 2515511210043330985984000000 :: IntegerTest> Test>Пример запуска программы на исполнениеКубенский">