Презентация на тему Знакомство с системами счисления

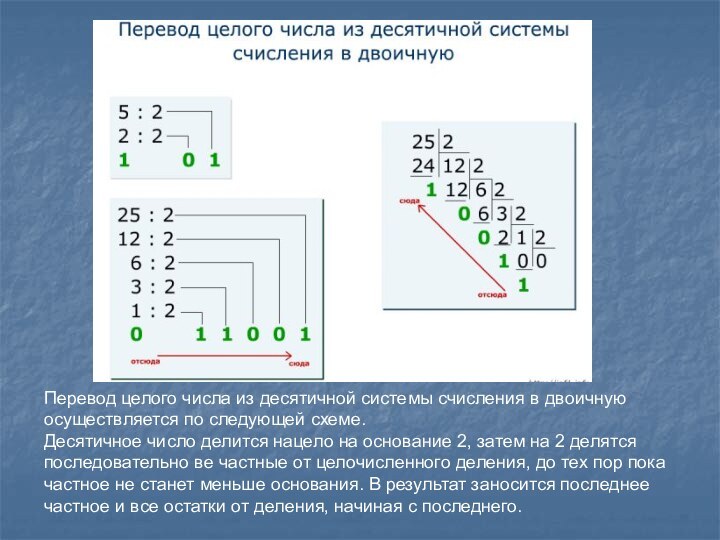
в себя ряд базисных чисел и правила записи всех

остальных.

В позиционных системах счисления значение каждой цифры (ее вес) изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Если это условие не выполняется, то система счисления является непозиционной. Например, в римской системе счисления любое число получается путем сложения или вычитания базисных чисел.

более старшего разряда, называется основанием позиционной системы, а сама

система счисления называется K-ичной. Например, основанием десятичной системы счисления является число 10; двоичной - число 2 и т.п.
Числа можно записать как суммы степеней не только числа 10, но и любого другого натурального числа, большего единицы.
Запись произвольного числа X в K-ичной позиционной системе счисления основывается на представлении этого числа в виде полинома.

осуществлять для целой и дробной частей числа по одному

алгоритму путем вычисления суммы произведений цифры двоичного числа на вес ее знакоместа.

двоичную осуществляется по следующей схеме.
Десятичное число делится нацело на

основание 2, затем на 2 делятся последовательно ве частные от целочисленного деления, до тех пор пока частное не станет меньше основания. В результат заносится последнее частное и все остатки от деления, начиная с последнего.

десять единиц каждого разряда объединяются в одну единицу соседнего

старшего разряда. Таким образом, каждый разряд имеет вес, равный степени 10. Например, в числе 262.27 цифра 2 повторена три раза, при этом самая левая цифра 2 означает количество сотен (ее вес равен 102); цифра 2, стоящая перед точкой, означает количество единиц (ее вес равен 100), а самая правая цифра 2 (после точки) - количество десятичных долей единицы (ее вес равен 10-1), так что последовательность цифр 262.27 представляет собой сокращенную запись выражения:
2*102 + 6*101 + 2*100 + 2*10-1 + 7*10-2.
В полиноме десятичного числа каждый коэффициент ai может быть одним из чисел, для обозначения которых введены специальные знаки.