Презентация на тему ეკონომიკისა და ბიზნესის სტატისტიკა. ცენტრალური ტენდენციის მახასიათებლები. თემა 2

ფერი

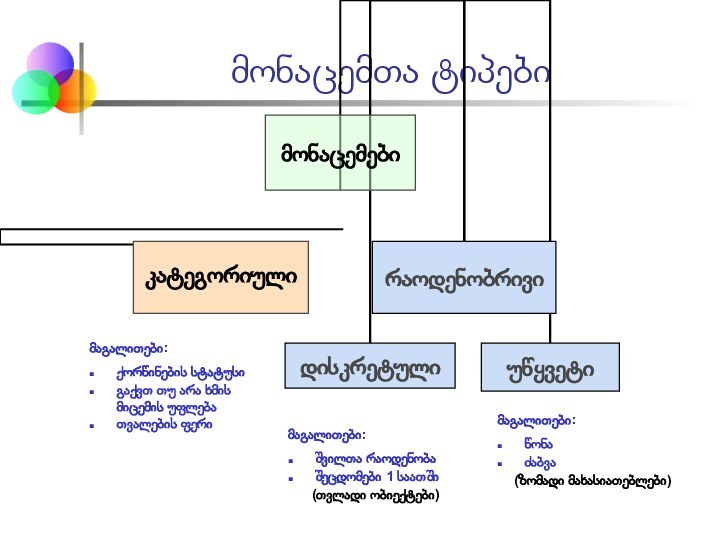
მაგალითები:
შვილთა რაოდენობა
შეცდომები 1 საათში

მაგალითები:
წონა
ძაბვა
(ზომადი მახასიათებლები)

ტენდენცია
გაფანტულობა

დაკვირვება
არითმეტიკული საშუალო

მნიშვნელობათა პოპულაციისათვის:




n ზომის შერჩევისათვის:

შერჩევის ზომა
დაკვირვების ობიექტები
პოპულაციის ზომა
პოპულაციის მნიშვნელობები

ექსტრემალური (ამოვარდნილი) მნიშვნელობების (outliers) გამო

(გაგრძ.)

0 1 2

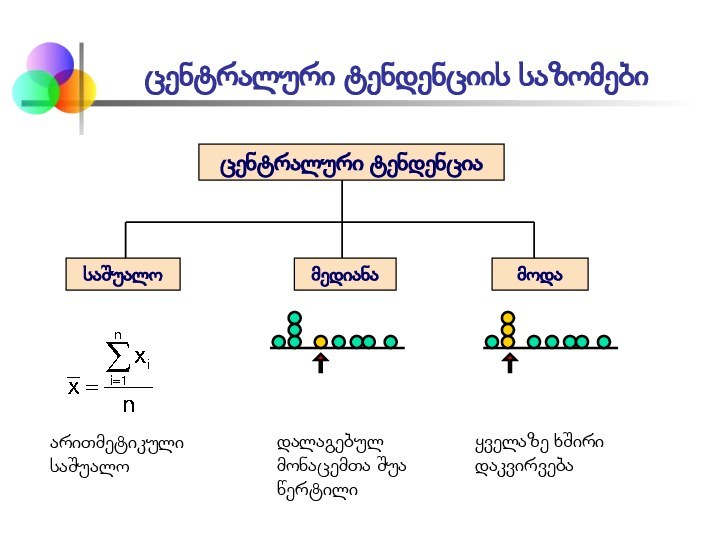
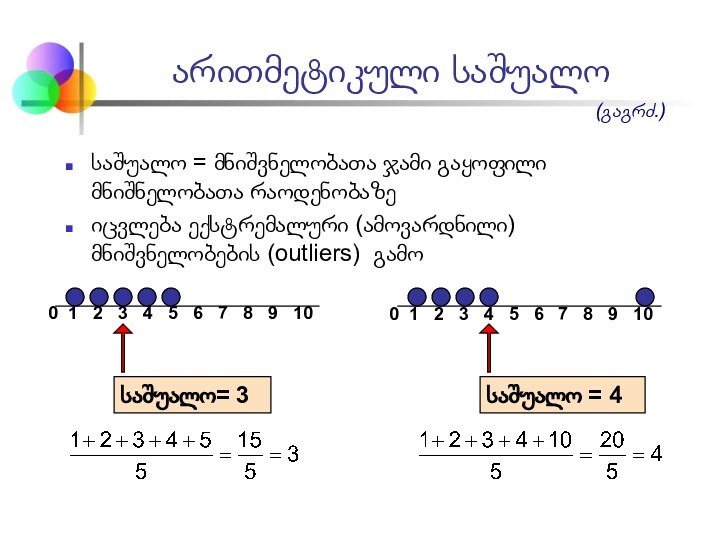
საშუალო= 3

0 1 2 3 4 5 6 7 8 9 10

საშუალო = 4

რიცხვი (50% მის ზემოთ და 50% ქვემოთ)





ხდება

0 1 2 3 4 5 6 7 8 9 10

Median = 3

0 1 2 3 4 5 6 7 8 9 10

Median = 3

რიცხვთა ოდენობა ლუწია, მედიანა არის ორი შუა წერტილის საშუალო


მედიანის

არ აქვს
გამოიყენება რაოდენობრივი და კატეგორიული მონაცემებისათვის
შესაძლებელია გვქონდეს რამდენიმე ან

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14

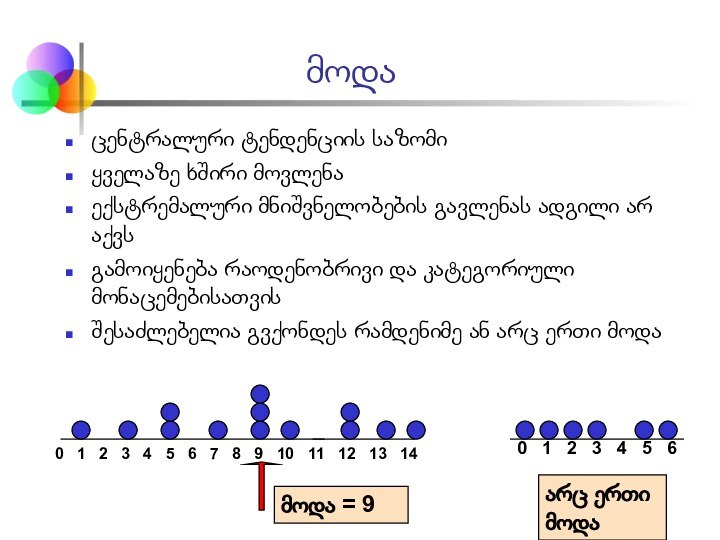
მოდა = 9

0 1 2 3 4 5 6

არც ერთი მოდა

500,000 300,000

მონაცემთა შუა წერტილი

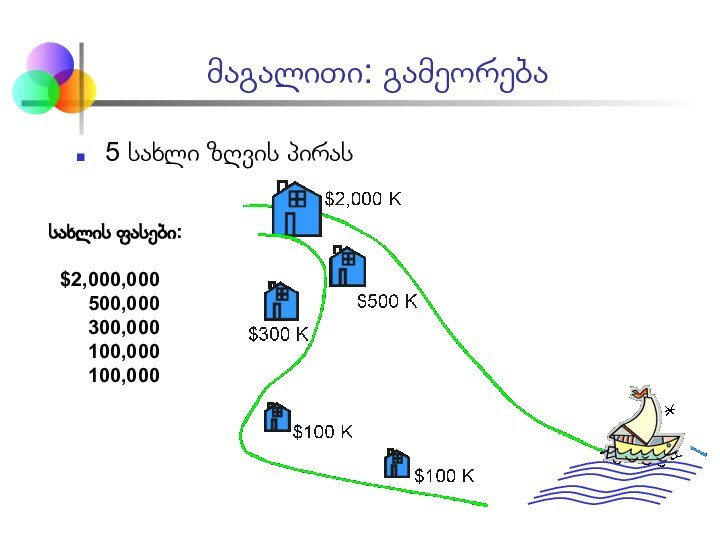
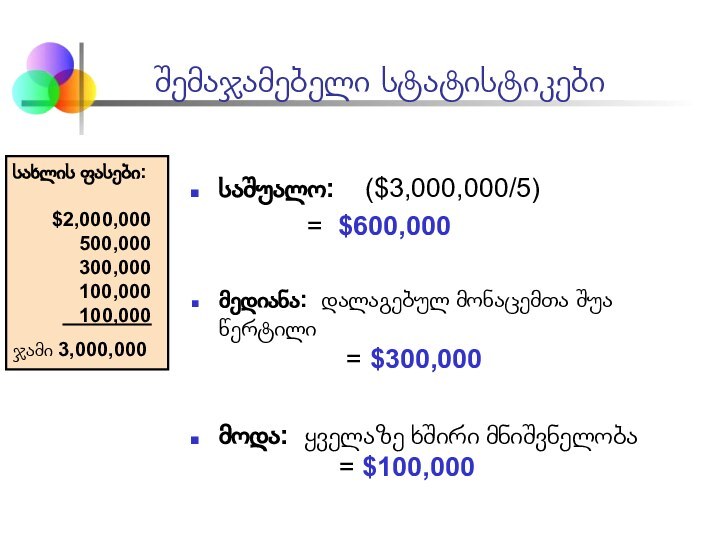
სახლის ფასები: $2,000,000
500,000 300,000 100,000 100,000
ჯამი 3,000,000

შემთხვევაში გამოიყენება მედიანა, რადგან ის არ არის მგრძნობიარე ამოვარდნილი

მდებარეობის რომელი საზომია “საუკეთესო”?

რომლებიც შეიცავს მნიშნელობათა თანაბარ რაოდენობებს.

25%

პირველი კვარტილი, Q1, არის

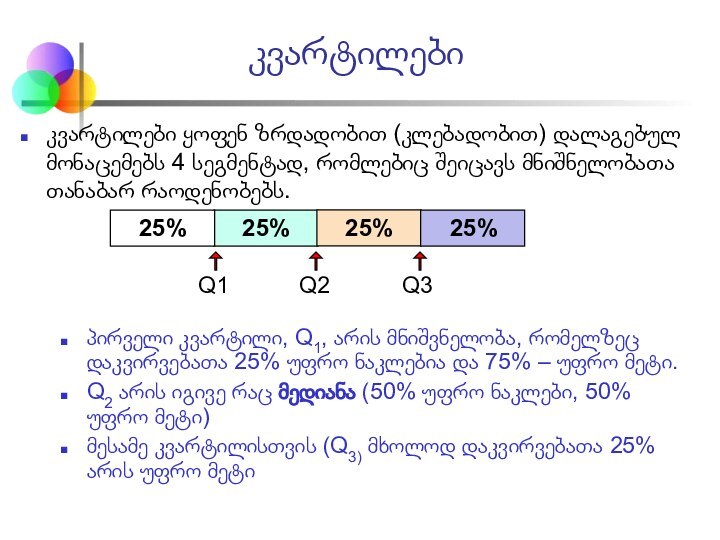
Q1

Q2

Q3

25%

25%

25%