Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему по математике на отработку заданий ЕГЭ №1-4

Содержание

2. Наиболее часто встречаются задания
3. №1. Теплоход рассчитан на 750 пассажиров и
4. №2. Флакон шампуня стоит 160 рублей. Какое
5. №3. В пачке 500 листов бумаги формата
6. №4. Аня купила проездной билет на месяц
7. Решение.Сумма кредита: 12 000 руб. – 100%Процентная
8. №6. Больному прописано лекарство, которое нужно пить
9. 7. На рисунке показано изменение температуры воздуха
11. 5. На графике, изображенном на рисунке, представлено
12. Решаем самостоятельно. 10. На рисунке жирными точками
13. Аннотация.На клетчатой бумаге с клетками размером 1
14. Площадь произвольного треугольникаПусть а − сторона треугольника,
15. Площадь параллелограммаПусть а − сторона параллелограмма, hа
16. Площадь трапецииПусть а и b − основания
17. Задание №311. Найдите площадь треугольника, изображенного на
18. Задание №312. Найдите площадь треугольника, изображенного на
19. Задание №313. Найдите площадь треугольника, изображенного на
20. Задание №314. Найдите площадь треугольника, изображенного на
21. Задание №315. Найдите площадь ромба, изображенного на
22. Задание №316. Найдите площадь четырехугольника, изображенного на
23. Задание №3Ответ: 36. Решение: 72816. Найдите площадь
24. Задание №317. Найдите площадь параллелограмма, изображенного на
25. Задание №318. Найдите площадь четырехугольника, изображенного на
26. На клетчатой бумаге с клетками размером 1
27. На клетчатой бумаге с клетками размером 1
28. Определение вероятностиВероятностью события A называют отношение числа
29. Свойства вероятностиСвойство 1. Вероятность достоверного события
30. В чемпионате по гимнастике участвуют 20 спортсменок:
31. В среднем из 1000 садовых насосов, поступивших
32. Решение: 100 + 8 = 108 –
33. В соревнованиях по толканию ядра участвуют 4
34. Научная конференция проводится в 5 дней. Всего
35. На семинар приехали 3 ученых из Норвегии,
36. Перед началом первого тура чемпионата по бадминтону
37. В сборнике билетов по математике всего 25
38. На клавиатуре телефона 10 цифр, от 0
39. Решение: Машин желтого цвета с черными надписями
40. ЗаданиРешение: 10, 11, 12, 13, 14, 15,
41. В случайном эксперименте симметричную монету бросают дважды.
42. В случайном эксперименте симметричную монету бросают дважды.
43. Решение: На циферблате между десятью часами и
44. Используемые материалыЕГЭ 2012. Математика. Задача В10. Теория
45. Скачать презентацию
46. Похожие презентации

Наиболее часто встречаются задания двух типов:В заданиях типа «Сколько карандашей по цене 2 рубля можно купить на 5 рублей?» ответ 2 карандаша – округляем до ближайшего меньшего целого, т.к. половину карандаша купить нельзя.В

Главная
Математика
Презентация по математике на отработку заданий ЕГЭ №1-4

Решение заданий по материалам открытого банка задач ЕГЭ по

Наиболее часто встречаются задания двух типов:В заданиях типа «Сколько

№1. Теплоход рассчитан на 750 пассажиров и 25 членов команды. Каждая спасательная

№2. Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить

№3. В пачке 500 листов бумаги формата А4. За неделю в офисе

№4. Аня купила проездной билет на месяц и сделала за месяц 41 поездку.

Решение.Сумма кредита: 12 000 руб. – 100%Процентная ставка: – 16%

№6. Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза

7. На рисунке показано изменение температуры воздуха на протяжении трех суток. По

Презентация по математике на отработку заданий ЕГЭ №1-4

5. На графике, изображенном на рисунке, представлено изменение биржевой стоимости акций нефтедобывающей

Решаем самостоятельно. 10. На рисунке жирными точками показано суточное количество осадков, выпадавших

Аннотация.На клетчатой бумаге с клетками размером 1 см 1 см изображены различные фигуры.

Площадь произвольного треугольникаПусть а − сторона треугольника, hа – высота, проведенная к

Площадь параллелограммаПусть а − сторона параллелограмма, hа – высота, проведенная к этой

Площадь трапецииПусть а и b − основания трапеции, h – высота, S

Задание №311. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки

Задание №312. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки

Задание №313. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки

Задание №314. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки

Задание №315. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки

Задание №316. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Задание №3Ответ: 36. Решение: 72816. Найдите площадь трапеции, изображенной на клетчатой бумаге

Задание №317. Найдите площадь параллелограмма, изображенного на клетчатой бумаге с размером клетки

Задание №318. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

На клетчатой бумаге с клетками размером 1 см 1 см изображена фигура (см.

Определение вероятностиВероятностью события A называют отношение числа m благоприятствующих этому событию исходов

Свойства вероятностиСвойство 1. Вероятность достоверного события

В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из

В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите

Решение: 100 + 8 = 108 – сумок всего (качественных и со

В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов

Научная конференция проводится в 5 дней. Всего запланировано 75 докладов − первые три

На семинар приехали 3 ученых из Норвегии, 3 из России и 4

Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары

В сборнике билетов по математике всего 25 билетов, в 10 из них

На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того,

Решение: Машин желтого цвета с черными надписями 23, всего машин 50. Поэтому

ЗаданиРешение: 10, 11, 12, 13, 14, 15, 16, 17, 18, 19Р =

В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что наступит

В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел

Решение: На циферблате между десятью часами и одним часом три часовых деления.

Используемые материалыЕГЭ 2012. Математика. Задача В10. Теория вероятностей. Рабочая тетрадь / Под

Интернет-ресурсы:Открытый банк заданий ЕГЭ по математикеОбразовательный портал для подготовки к экзаменам «РЕШУ

Слайды презентации

Слайд 2 Наиболее часто встречаются задания двух

типов:
В заданиях типа «Сколько карандашей по цене 2 рубля

можно купить на 5 рублей?» ответ 2 карандаша – округляем до ближайшего меньшего целого, т.к. половину карандаша купить нельзя.
В заданиях типа «Сколько двухлитровых банок потребуется, чтобы в них поместилось 5 литров воды» ответ 3 – округляем до ближайшего большего целого, т.к. вся вода должна поместиться.
Важно не путать эти два случая, округляя в ту или иную сторону.

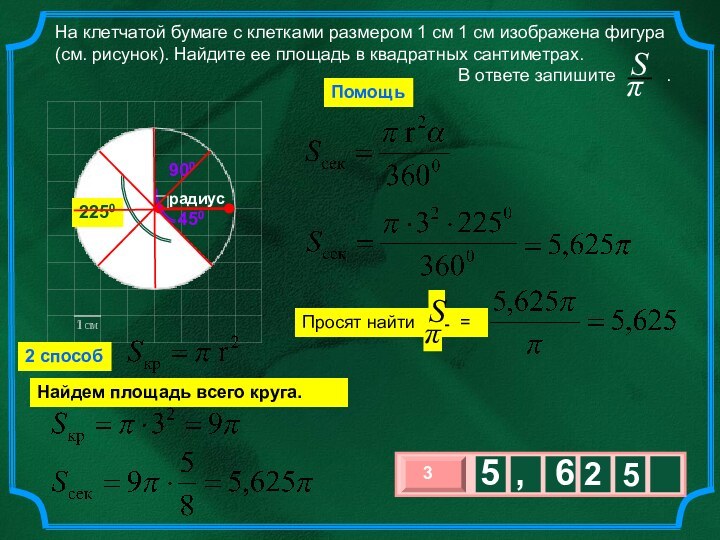
Особенности экзаменационных заданий: Округление

Слайд 3 №1. Теплоход рассчитан на 750 пассажиров и 25

№1. Теплоход рассчитан на 750 пассажиров и 25 членов команды. Каждая

членов команды. Каждая спасательная шлюпка может вместить 70 человек.

Какое наименьшее число шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и всех членов команды?

Решение.
Всего на теплоходе 750 + 25 = 775 человек.
Разделим 775 на 70:

Ни один человек не должен погибнуть. 11 шлюпок будут заполнены полностью и еще останется 5 человек, для которых, нам потребуется еще одна шлюпка. Значит, на судне должно быть не менее 12 шлюпок.

Ответ: 12.

Слайд 4 №2. Флакон шампуня стоит 160 рублей. Какое наибольшее

№2. Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно

число флаконов можно купить на 1000 рублей во время

распродажи, когда скидка составляет 25%?

Решение.
Флакон шампуня: 160 руб. – 100%
Скидка: ? руб. – 25%
Новая цена шампуня: х руб. – 75%

Узнаем новую цену шампуня:

Разделим 1000 на 120:

Значит, на 1000 рублей можно будет купить не более 8 флаконов шампуня.

Ответ: 8.

−

Слайд 5 №3. В пачке 500 листов бумаги формата А4.

№3. В пачке 500 листов бумаги формата А4. За неделю в

За неделю в офисе расходуется 1200 листов. Какое наименьшее

количество пачек бумаги нужно купить в офис на 4 недели?

Решение.
Всего за 4 недели в офисе расходуется 1200 ∙ 4 = 4800 листов бумаги. Разделим 4800 на 500:

Значит, для того, чтобы обеспечить офис бумагой на 4 недели нужно купить не менее 10 пачек.

Ответ: 10.

Слайд 6 №4. Аня купила проездной билет на месяц и

№4. Аня купила проездной билет на месяц и сделала за месяц 41

сделала за месяц 41 поездку. Сколько рублей она сэкономила, если

проездной билет на месяц стоит 580 рублей, а разовая поездка − 20 рублей?

Решение.

Если бы Аня оплачивала каждую свою поездку по тарифу 20 рублей, то она бы потратила
41 ∙ 20 = 820 рублей,
но поскольку Аня купила проездной, то ее экономия составила:
820 – 580 = 240 рублей.

Ответ: 240.

Слайд 7 Решение.
Сумма кредита: 12 000 руб. – 100%
Процентная ставка: –

16%
Общая сумма возврата: х

руб. – 116%

Узнаем, какую сумму нужно вернуть клиенту в банк:

Разделим эту сумму на 12 месяцев:
13920 : 12 = 1160 рублей составляет ежемесячный взнос в банк.

№5. Клиент взял в банке кредит 12 000 рублей на год под 16%. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, с тем чтобы через год выплатить всю сумму, взятую в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно?

Ответ: 1160.

Слайд 8 №6. Больному прописано лекарство, которое нужно пить по

№6. Больному прописано лекарство, которое нужно пить по 0,5 г 3

0,5 г 3 раза в день в течение 21

дня. В одной упаковке 10 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения?

Решение.
За весь курс лечения больному необходимо выпить
0,5 · 3 · 21 = 31,5 г лекарства.
В одной упаковке содержится:
0,5 · 10 = 5 г лекарства.
Разделим 31,5 на 5:

Значит, на курс лечения больному необходимо не менее 7 упаковок лекарства.

Ответ: 7.

Слайд 9 7. На рисунке показано изменение температуры воздуха на

7. На рисунке показано изменение температуры воздуха на протяжении трех суток.

протяжении трех суток. По горизонтали указывается дата и время

суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей температурами воздуха 22 января.

(- 10)

(- 23)

= 13

Ответ: 13

Слайд 10 8. Первый посев семян петрушки рекомендуется проводить в

апреле при дневной температуре воздуха не менее +6° С.

На рисунке показан прогноз дневной температуры воздуха в первых трех неделях апреля. Определите, в течение скольких дней за этот период можно производить посев петрушки.

Ответ: 11

Слайд 11 5. На графике, изображенном на рисунке, представлено изменение

5. На графике, изображенном на рисунке, представлено изменение биржевой стоимости акций

биржевой стоимости акций нефтедобывающей компании в первые две недели

сентября. 3 сентября бизнесмен приобрел 10 акций этой компании. Шесть из них он продал 10 сентября, а 12 сентября продал остальные 4. Сколько рублей потерял бизнесмен в результате этих операций?

4 5 6 7 8 9 10 11 12 13

10 * 800=8000 р.

6 * 400=2400 р.

4 * 600=2400 р.

8000 – 4800=3200 р.

Ответ: 3200

800

600

400

Слайд 12 Решаем самостоятельно.
10. На рисунке жирными точками показано

Решаем самостоятельно. 10. На рисунке жирными точками показано суточное количество осадков,

суточное количество осадков, выпадавших в Казани с 3 по

15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода не выпадало осадков.

Слайд 13 Аннотация.

На клетчатой бумаге с клетками размером 1 см

Аннотация.На клетчатой бумаге с клетками размером 1 см 1 см изображены различные

1 см изображены различные фигуры. Необходимо найти площадь. Ответ записать

в квадратных сантиметрах.

Для того, чтобы быстро решать такие задания, надо знать формулы для вычисления площадей треугольника, прямоугольника, трапеции, параллелограмма, квадрата.

Часто при решении таких задач используются свойства площадей. Фигуру надо разбить на части, площади которых можно найти по знакомым формулам. Или наоборот, фигуру надо достроить. Получится большая фигура, площадь которой мы сможем найти.

Слайд 14 Площадь произвольного треугольника

Пусть а − сторона треугольника, hа

Площадь произвольного треугольникаПусть а − сторона треугольника, hа – высота, проведенная

– высота, проведенная к этой стороне, S − его

площадь.
Тогда справедлива формула:

Слайд 15

Площадь параллелограмма

Пусть а − сторона параллелограмма, hа –

Площадь параллелограммаПусть а − сторона параллелограмма, hа – высота, проведенная к

высота, проведенная к этой стороне, S − его площадь.

Тогда справедлива формула:

S = aha

Слайд 16
Площадь трапеции

Пусть а и b − основания трапеции,

Площадь трапецииПусть а и b − основания трапеции, h – высота,

h – высота,
S − площадь трапеции.
Тогда справедлива

формула:

Слайд 17 Задание №3

11. Найдите площадь треугольника, изображенного на клетчатой

Задание №311. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером

бумаге с размером клетки 1см×1см. Ответ дайте в квадратных

сантиметрах.

Ответ: 16.

Решение:

Слайд 18 Задание №3

12. Найдите площадь треугольника, изображенного на клетчатой

Задание №312. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером

бумаге с размером клетки 1см×1см. Ответ дайте в квадратных

сантиметрах.

Ответ: 12.

Решение:

Слайд 19 Задание №3

13. Найдите площадь треугольника, изображенного на клетчатой

Задание №313. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером

бумаге с размером клетки 1см×1см. Ответ дайте в квадратных

сантиметрах.

Ответ: 12.

Решение:

Слайд 20 Задание №3

14. Найдите площадь треугольника, изображенного на клетчатой

Задание №314. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером

бумаге с размером клетки 1см×1см. Ответ дайте в квадратных

сантиметрах.

Ответ: 33.

Решение:

Слайд 21 Задание №3

15. Найдите площадь ромба, изображенного на клетчатой

Задание №315. Найдите площадь ромба, изображенного на клетчатой бумаге с размером

бумаге с размером клетки 1см×1см. Ответ дайте в квадратных

сантиметрах.

Ответ: 16.

Решение:

Слайд 22 Задание №3

16. Найдите площадь четырехугольника, изображенного на клетчатой

Задание №316. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером

бумаге с размером клетки 1см×1см. Ответ дайте в квадратных

сантиметрах.

Ответ: 8.

Решение:

Слайд 23
Задание №3

Ответ: 36.
Решение:

7
2

8

16. Найдите площадь трапеции,

изображенной на клетчатой бумаге с размером клетки 1см×1см. Ответ

дайте в квадратных сантиметрах.

Слайд 24 Задание №3

17. Найдите площадь параллелограмма, изображенного на клетчатой

Задание №317. Найдите площадь параллелограмма, изображенного на клетчатой бумаге с размером

бумаге с размером клетки 1см×1см. Ответ дайте в квадратных

сантиметрах.

Ответ: 28.

Решение:

Слайд 25

Задание №3

18. Найдите площадь четырехугольника, изображенного на клетчатой

Задание №318. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером

бумаге с размером клетки 1см×1см. Ответ дайте в квадратных

сантиметрах.

Ответ: 14,5.

Решение:

Слайд 26 На клетчатой бумаге с клетками размером 1 см

На клетчатой бумаге с клетками размером 1 см 1 см изображена фигура

1 см изображена фигура (см. рисунок). Найдите ее площадь в

квадратных сантиметрах.
В ответе запишите .

радиус

Слайд 27 На клетчатой бумаге с клетками размером 1 см

1 см изображена фигура (см. рисунок). Найдите ее площадь в

квадратных сантиметрах.
В ответе запишите .

радиус

900

450

Слайд 28 Определение вероятности
Вероятностью события A называют отношение числа m

Определение вероятностиВероятностью события A называют отношение числа m благоприятствующих этому событию

благоприятствующих этому событию исходов к общему числу n всех

равновозможных несовместимых событий, которые могут произойти в результате одного испытания или наблюдения:

Пусть k – количество бросков монеты, тогда количество всевозможных исходов: n = 2k.

Пусть k – количество бросков кубика, тогда количество всевозможных исходов: n = 6k.

Слайд 29 Свойства вероятности
Свойство 1. Вероятность достоверного события

равна единице: Р(А) = 1.

Свойство 2. Вероятность невозможного события равна нулю: Р(А) = 0.

Свойство 3. Вероятность случайного события есть
положительное число, заключенное между
нулем и единицей: 0 ≤ Р(А) ≤ 1.

Слайд 30 В чемпионате по гимнастике участвуют 20 спортсменок: 8

В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7

из России, 7 из США, остальные − из Китая.

Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.

Решение.
Всего участвует 20 спортсменок,
из которых 20 – 8 – 7 = 5 спортсменок из Китая.
Вероятность того, что спортсменка, выступающая первой, окажется из Китая, равна 5/20 = 1/4 = 0,25.

Ответ: 0,25.

Задани

Слайд 31 В среднем из 1000 садовых насосов, поступивших в

В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают.

продажу, 5 подтекают. Найдите вероятность того, что один случайно

выбранный для контроля насос не подтекает.

Решение:
1000 – 5 = 995 – насосов не подтекают.
Вероятность того, что один случайно выбранный для контроля насос не подтекает, равна
995/1000 = 0,995.

Ответ: 0,995.

Задани

Слайд 32 Решение:
100 + 8 = 108 – сумок

Решение: 100 + 8 = 108 – сумок всего (качественных и

всего (качественных и со скрытыми дефектами).
Вероятность того, что купленная

сумка окажется качественной, равна 100/108 = 0,(925) ≈ 0,93.

Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.

Ответ: 0,93.

Задани

Слайд 33 В соревнованиях по толканию ядра участвуют 4 спортсмена

В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7

из Финляндии, 7 спортсменов из Дании, 9 спортсменов из

Швеции и 5 − из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.

Ответ: 0,36.

Задани

Решение:
Всего участвует 4 + 7 + 9 + 5 = 25 спортсменов. Вероятность того, что спортсмен, который выступает последним, окажется из Швеции, равна
9/25 = 36/100 = 0,36.

Слайд 34 Научная конференция проводится в 5 дней. Всего запланировано

Научная конференция проводится в 5 дней. Всего запланировано 75 докладов − первые

75 докладов − первые три дня по 17 докладов, остальные распределены

поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?

Ответ: 0,16.

Задани

Решение:
В последний день конференции запланировано
(75 – 17 × 3) : 2 = 12 докладов.
Вероятность того, что доклад профессора М. окажется запланированным на последний день конференции, равна 12/75 = 4/25 = 0,16.

Слайд 35 На семинар приехали 3 ученых из Норвегии, 3

На семинар приехали 3 ученых из Норвегии, 3 из России и

из России и 4 из Испании. Порядок докладов определяется

жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад ученого из России.

Ответ: 0,3.

Задани

Решение:
Всего участвует 3 + 3 + 4 = 10 ученых.
Вероятность того, что восьмым окажется доклад ученого из России, равна 3/10 = 0,3.

Слайд 36 Перед началом первого тура чемпионата по бадминтону участников

Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые

разбивают на игровые пары случайным образом с помощью жребия.

Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?

Ответ: 0,36.

Задани

Решение:
Нужно учесть, что Руслан Орлов должен играть с каким-либо бадминтонистом из России. И сам Руслан Орлов тоже из России.
Вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России, равна 9/25 = 36/100 = 0,36.

Слайд 37 В сборнике билетов по математике всего 25 билетов,

В сборнике билетов по математике всего 25 билетов, в 10 из

в 10 из них встречается вопрос по неравенствам. Найдите

вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам.

Ответ: 0,6.

Задани

Решение:
25 – 10 = 15 – билетов не содержат вопрос по неравенствам.
Вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам, равна
15/25 = 3/5 = 0,6.

Слайд 38 На клавиатуре телефона 10 цифр, от 0 до

На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность

9. Какова вероятность того, что случайно нажатая цифра будет

чётной?

Ответ: 0,5.

Задани

Решение:
Количество четных цифр на клавиатуре равно 5:
0, 2, 4, 6, 8
всего же цифр на клавиатуре 10, тогда вероятность что случайно нажатая цифра будет чётной равна
5/10 = 0,5.

Слайд 39 Решение:
Машин желтого цвета с черными надписями 23,

Решение: Машин желтого цвета с черными надписями 23, всего машин 50.

всего машин 50. Поэтому вероятность того, что на случайный

вызов приедет машина желтого цвета с черными надписями, равна:
P = 23 : 50 = 0,46.

В фирме такси в наличии 50 легковых автомобилей; 27 из них чёрные с жёлтыми надписями на бортах, остальные – жёлтые с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.

Ответ: 0,46.

Задани

Слайд 40 Задани
Решение:
10, 11, 12, 13, 14, 15, 16,

17, 18, 19

Р = = 0,3

Ответ: 0,3.
Какова

вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на три?

Слайд 41 В случайном эксперименте симметричную монету бросают дважды. Найдите

В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что

вероятность того, что наступит исход ОР (в первый раз

выпадает орёл, во второй – решка).

Решение.
Всего 4 варианта: о; о о; р р; р р; о.
Благоприятных 1: о; р.
Вероятность равна 1/4 = 0,25.

Задани

Ответ: 0,25.

Слайд 42 В случайном эксперименте симметричную монету бросают дважды. Найдите

вероятность того, что орел выпадет ровно один раз.
Решение.
Всего 4

варианта: о; о о; р р; р р; о.
Благоприятных 2: о; р и р; о.
Вероятность равна 2/4 = 1/2 = 0,5.

Задани

Ответ: 0,5.

Слайд 43 Решение:
На циферблате между десятью часами и одним

Решение: На циферблате между десятью часами и одним часом три часовых

часом три часовых деления. Всего на циферблате 12 часовых

делений.
Поэтому искомая вероятность равна:

Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 10, но не дойдя до отметки 1 час.

Ответ: 0,25.

Задани

Слайд 44 Используемые материалы
ЕГЭ 2012. Математика. Задача В10. Теория вероятностей.

Используемые материалыЕГЭ 2012. Математика. Задача В10. Теория вероятностей. Рабочая тетрадь /

Рабочая тетрадь / Под ред. А.Л. Семенова и И.В.

Ященко.− М.: МЦНМО, 2012. − 48 с.

ЕГЭ: 3000 задач с ответами по математике. Все задания группы В / под ред. А.Л. Семенова, И.В. Ященко. – 3-е изд., перераб. и доп. – М.: Издательство «Экзамен», 2012. – 543 с.

http://mathege.ru/or/ege/Main.html − Материалы открытого банка заданий по математике 2013 года

http://reshuege.ru/ − Сайт Дмитрия Гущина