Слайд 2
2017 год
«Дроби вокруг нас»
Общая характеристика проекта
Цель работы: повысить
интерес учащихся к теме «Дроби»
Задачи:
собрать дополнительный теоретический материал по
теме «Дроби»
сделать подборку нестандартных задач с дробями
найти незримую связь окружающего нас мира с миром дробных чисел
создать электронную презентацию по нашему проекту
продемонстрировать другим учащимся, что мир дробей может быть очень увлекательным
Тип проекта: практико-ориентированный.
Виды деятельности: творческий, информационный.
Применяемые умения:
– проектные (организационные, информационные, поисковые, коммуникативные, презентационные, )
– предметные (математические).
База выполнения: школьная.
Формы обучения: групповая и индивидуальная.
Продолжительность выполнения: средняя продолжительность – один месяц.
Средства обучения: печатные, наглядные, компьютерные презентации.
Формы продуктов деятельности: электронная презентация
Как возникли дроби.
Дроби возникли в глубокой древности, так как натуральные числа не могли с необходимой точностью давать ответ при измерениях и вычислениях. Сначала появились дроби с числителем 1. Все остальные выражали через них.
Человек, который умел выполнять действия с дробями был как правило жрецом, т.е. считался почти магом. Современное обозначение дробей пришло из Древней Индии. Только в начале запись обыкновенной дроби не содержала дробной черты. Черта дроби получила свое распространение только около 400 лет назад. Названия числитель и знаменатель ввел в 18 веке греческий монах -Максим Плануд .
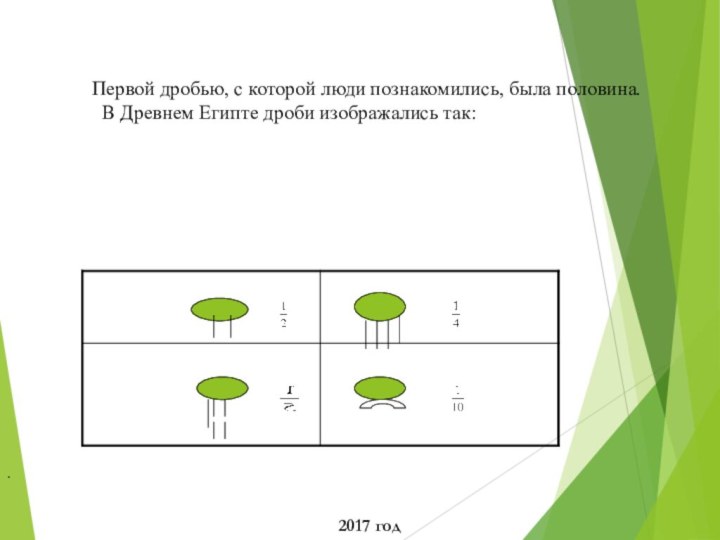
Первой дробью, с которой люди познакомились, была половина.
В Древнем Египте дроби изображались так:
Слайд 7
2017 год
.
Как раньше записывали дроби.
Диофант (3 век
н.э.) дроби записывал почти также как и мы, только
над чертой писал знаменатель, а под чертой - числитель или записывал числитель, частица и затем знаменатель. Все народы называли дробь "ломаным числом".
Что такое обыкновенная дробь.
Обыкновенной дробью называют число, которое обозначает часть от целого или несколько частей от единого целого. Оно состоит из числителя и знаменателя. Записывается при помощи черты. Сверху пишется числитель, снизу – знаменатель.
Виды дробей.
1) Если числитель дроби меньше ее знаменателя , то дробь называется правильной.
2) Если числитель дроби больше ее знаменателя или равен ему, то дробь называется неправильной.
Перевод неправильной дроби в смешанную дробь — это выделение
натурального числа из дроби.
3) Если дробь состоит из натурального числа и правильной дроби , то такая дробь называется смешанной .
Основные свойства
дробей.
1) Числитель и знаменатель дроби можно умножать (делить) на одно и то же натуральное число, от этого величина дроби не изменяется.
Основное свойство дроби используется при сокращении дробей и при приведении двух и более дробей к одинаковому знаменателю.
2) Любое натуральное число можно записать в виде обыкновенной дроби со знаменателем 1 (единица). Такая дробь будет неправильной.
Применение дробей в
повседневной жизни.
Дроби и музыка.
Ноты отличаются по длительности их звучания. Знаком обозначаю целую ноту, нота вдвое короче – половинную - , четвертную - ,восьмую - , шестнадцатую - .
2) Золотое сечение
Математики древности и средневековья золотым сечением называли деление отрезка, при котором длина всего отрезка так относится к длине его большей части, как длина большей части к меньшей. Это отношение приближённо равно 0,618. Золотое сечение чаще всего применяется в произведениях искусства, архитектуре,также встречается в природе.
Окружающие нас предметы также часто дают примеры золотого сечения Например, переплёты многих книг имеют отношение ширины и длины, близкое к значению 0,618.
Красивейшее произведение древнегреческой архитектуры – Парфенон, построено в V в. до н.э., отношение высоты здания к его длине равно 0,618.
Слайд 13
2017 год
.
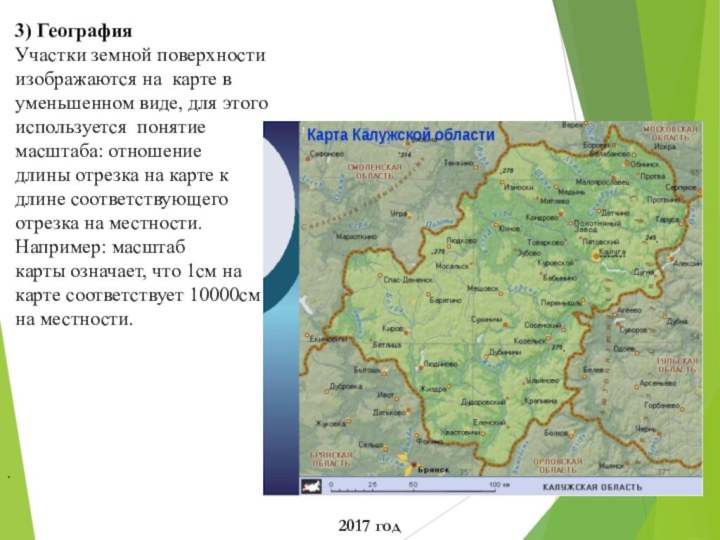
3) География
Участки земной поверхности изображаются
на карте в уменьшенном виде, для этого
используется понятие
масштаба:
отношение
длины отрезка на карте к
длине соответствующего
отрезка на местности.
Например: масштаб
карты означает, что 1см на
карте соответствует 10000см на местности.
Слайд 14
2017год
.
4) В строительстве.
Фасад здания Первой клинической больницы
им. Н.И. Пирогова (Москва) построен так, что если разделить
высоту здания по золотому сечению, то получим те или иные выступы, карнизы и т.д. Например, равны
отношения .
Применение.
На машиностроительных заводах есть очень такая увлекательная профессия, называется она - разметчик. Разметчик намечает на заготовке линии, по которым эту заготовку следует обрабатывать для того, чтобы придать ей необходимую форму.
Разметчику приходится решать интересные и нелегкие геометрические задачи, производить арифметические расчеты и т. д.
"Понадобилось как-то распределить 7 одинаковых прямоугольных пластинок равными долями между 12 деталями. Принесли эти 7 пластинок разметчику и попросили его, если можно, разметить пластинки так, чтобы не пришлось дробить ни одной из них на очень мелкие части. Значит, простейшее решение - резать каждую пластинку на 12 равных частей - не годилось, так как при этом получалось много мелких долей. Как же быть?
Возможно ли деление данных пластинок на более крупные доли? Разметчик подумал, произвел какие-то арифметические расчеты с дробями и нашел самый экономный способ деления данных пластинок.
Слайд 16
2017 год
.
Впоследствии он легко дробил 5
пластинок для распределения их равными долями между шестью деталями,
13 пластинок для 12 деталей, 13 пластинок для 36 деталей, 26 для 21 и т.п.
Оказывается, разметчик представил дробь 7\12 в виде суммы единичных дробей 1\3 + 1\4. Значит, если из 7 данных пластинок 4 разрезать на три равные части каждую, то получим 12 третей, то есть по одной трети для каждой детали. Остальные 3 пластинки разрежем 4 равные части каждую, получим 12 четвертей, то есть по одной четверти для каждой детали. Аналогично, используя представления дробей в виде суммы единичных дробей 5\6=1\2+1\3;
13\121\3+3\4;
13\36=1\4+1\9.
Слайд 18
Кто и как изобрел
десятичные дроби?
Из истории обыкновенных и
десятичных дробей.
В Древнем Китае уже пользовались десятичной системой мер, обозначали дробь словами, используя меры длины чи: цуни, доли, порядковые, шерстинки, тончайшие, паутинки. Дробь вида 2,135436 выглядела так: 2 чи, 1 цунь, 3 доли, 5 порядковых, 4 шерстинки, 3 тончайших, 6 паутинок. Так записывались дроби на протяжении двух веков, а в V веке китайский ученый Цзю-Чун-Чжи принял за единицу не чи, а чжан = 10 чи, тогда эта дробь выглядела так: 2 чжана, 1 чи, 3 цуня, 5 долей, 4 порядковых, 3 шерстинки, 6 тончайших, 0 паутинок.
Предшественниками десятичных дробей являлись шестидесятеричные дроби древних вавилонян. Некоторые элементы десятичной дроби встречаются в трудах многих ученых Европы в 12, 13, 14 веках.
Слайд 19
Десятичную дробь с помощью определенных знаков и цифр
попытался записать арабский математик ал-Уклисиди в X веке. Свои
мысли он выразил в "Книге разделов об индийской арифметике".
В XV веке, в Узбекистане, вблизи города Самарканда жил математик и астроном Джемшид Гиясэддин ал-Каши. Он наблюдал за движением звезд, планет и Солнца, в этой работе ему необходимы были десятичные дроби. Ал-Каши написал книгу "Ключ к арифметике" (была издана в 1424 году), в которой он показал запись дроби в одну строку числами в десятичной системе и дал правила действия с ними. Ученый пользовался несколькими способами написания дроби: то он применял вертикальную черту, то чернила черного и красного цветов. Но этот труд до европейских ученых своевременно не дошел.
Слайд 20
Примерно в это время математики Европы тоже пытались
найти удобную запись десятичной дроби. В книге "Математический канон"
французского математика Ф. Виета (1540-1603) десятичная дробь записана так 2 135436 - дробная часть и подчеркивалась и записывалась выше строки целой части числа.
В 1585 г., независимо от ал-Каши, фламандский ученый Симон Стевин (1548-1620) сделал важное открытие, о чем написал в своей книге "Десятая". Эта маленькая работа (всего 7 страниц) содержала объяснение записи и правил действий с десятичными дробями. Он писал цифры дробного числа в одну строку с цифрами целого числа, при этом нумеруя их. Например, число 12,761 записывалось так: 12076112 или число 0,3752 записывалось так: 3752.
Слайд 21
Именно Стевина считают изобретателем десятичных дробей.
Запятая в
записи дробей впервые встречается в 1592г., а в 1617г.
шотландский математик Джон Непер предложил отделять десятичные знаки от целого числа либо запятой, либо точкой.
Современную запись, т.е. отделение целой части запятой, предложил Кеплер (1571) - (1630 гг.).
В странах, где говорят по-английски (Англия, США, Канада и др.), и сейчас вместо запятой пишут точку, например: 2.3 и читают: два точка три.
Слайд 23
2017 год
.
Равные части арбуза – называют ДОЛЯМИ.
Так
как арбуз разделили на 6 долей, то одна доля
«одна шестая арбуза»
Слайд 24
2017 год
.
Записи вида называют
обыкновенными дробями.
Числитель дроби
Знаменатель дроби
Знаменатель дроби показывает
на сколько долей делят, а
числитель дроби
показывает – сколько таких долей взято.
Слайд 25
2017год
.
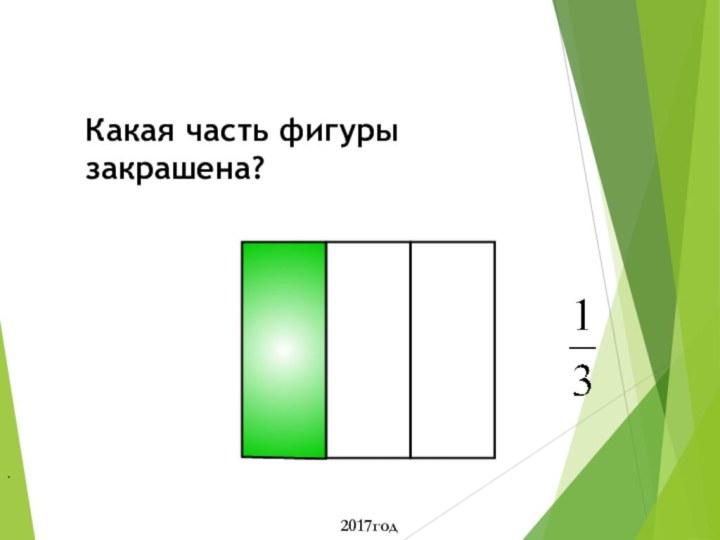
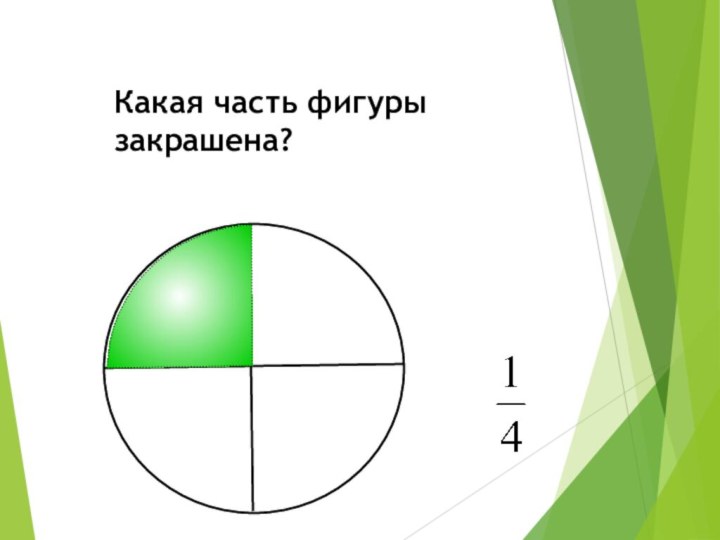
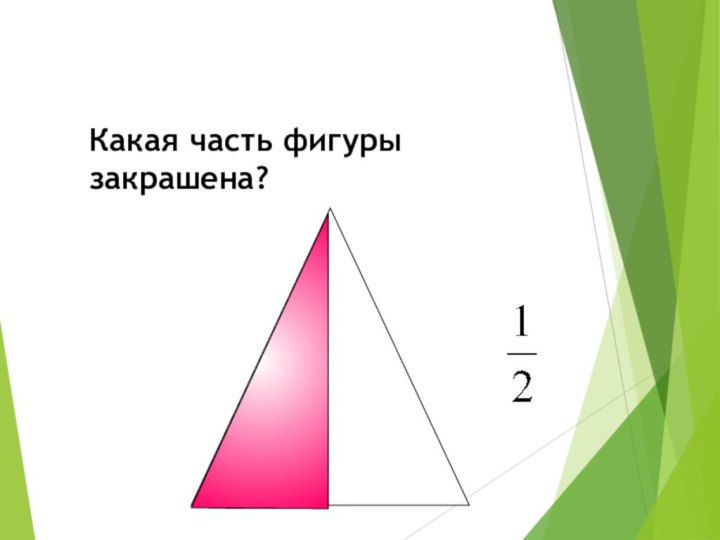
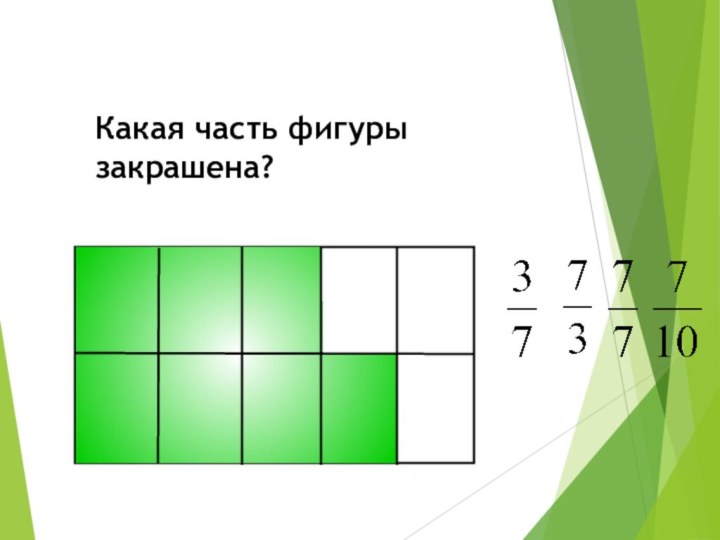
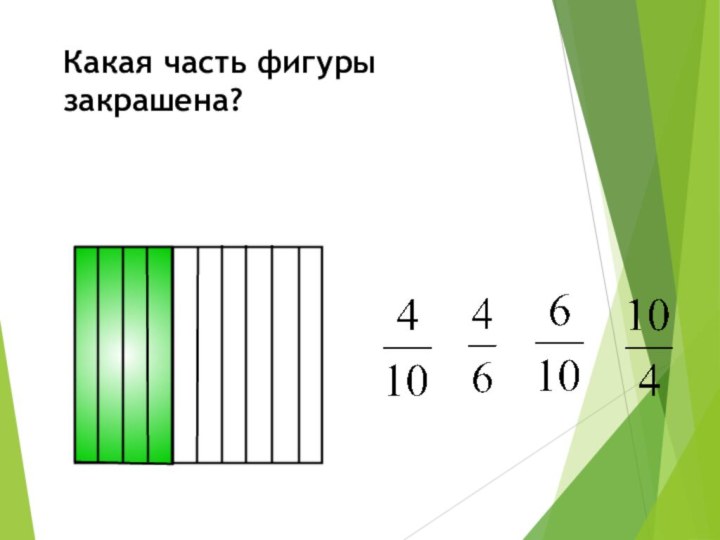
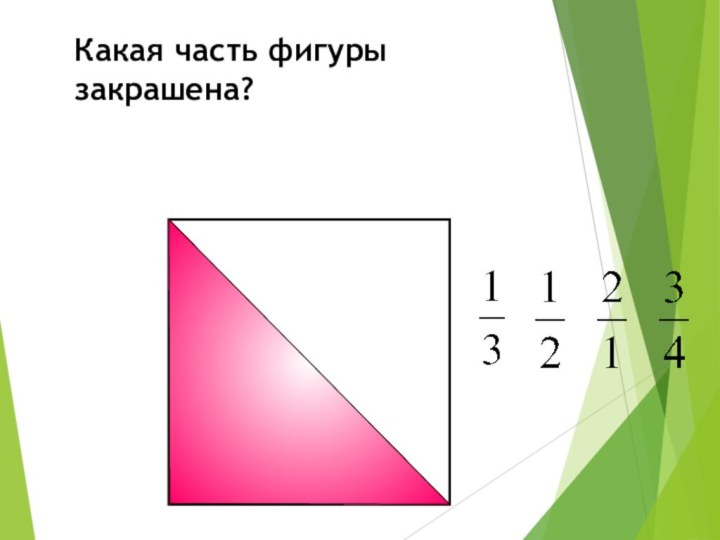
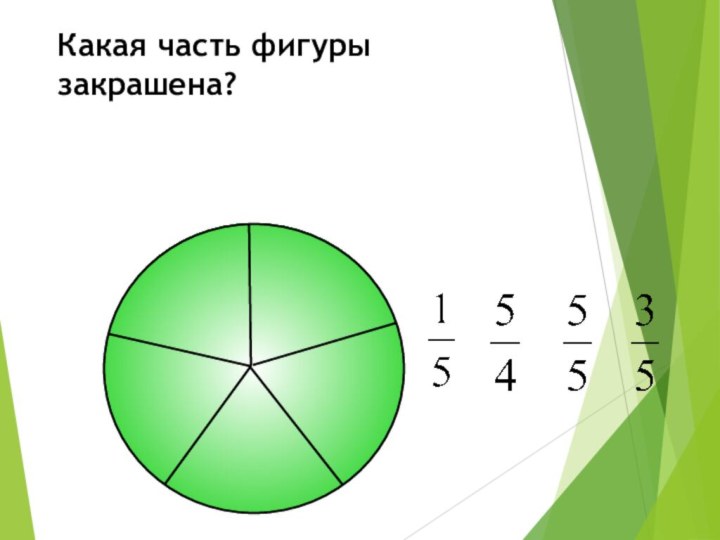
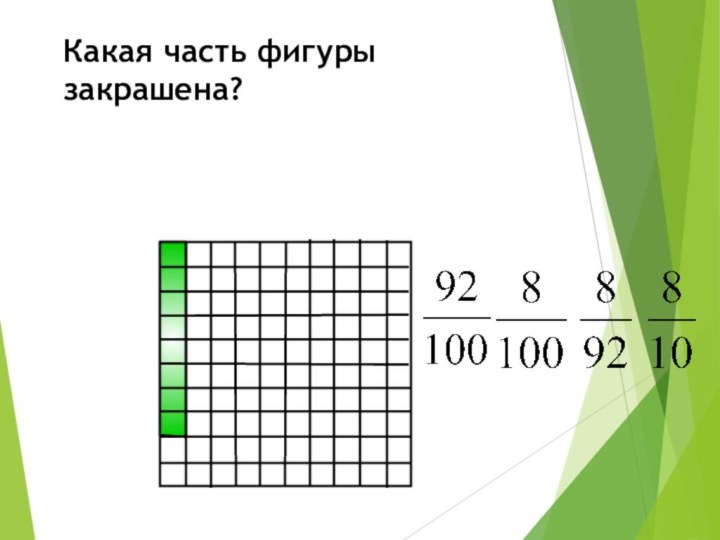
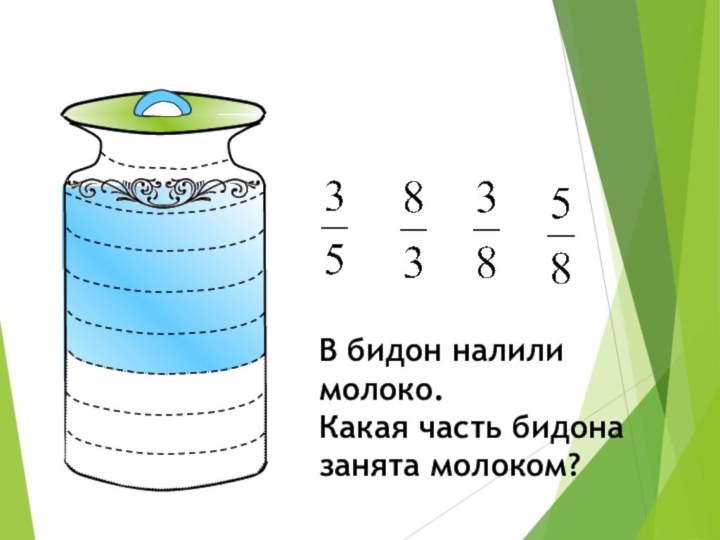
Какая часть фигуры закрашена?
Слайд 33
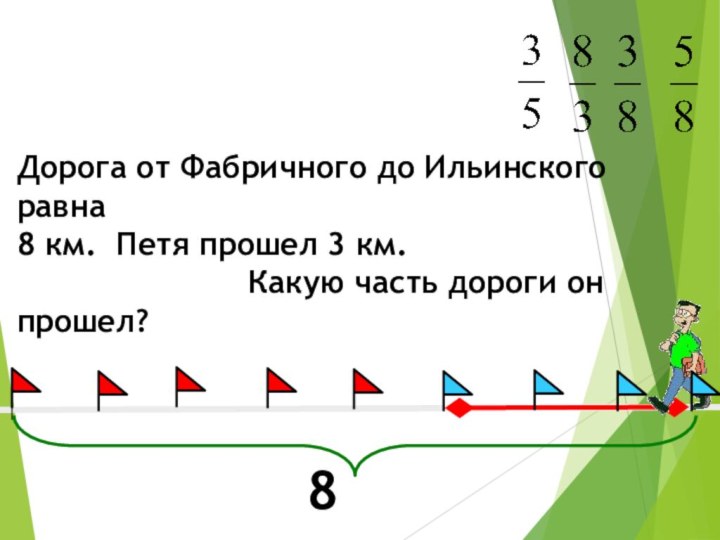
Дорога от Фабричного до Ильинского равна
8 км.
Петя прошел 3 км.
Какую часть дороги он прошел?
8 км