- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему проекта по математике Способы получения простых чисел
Содержание
- 2. Цель работыСоставить таблицу простых чисел от 1
- 3. Задачи работыИзучить тему «Простые числа»;Найти в научной
- 4. Определение простых чиселНатуральное число p называется простым,
- 5. Где применяются простые числа?В математике простые числа
- 6. Множество простых чисел бесконечноЭто доказал Евклид ещё три тысячи лет назад
- 7. Как получить простые числа?Решето Эратосфена Скатерть УламаФормула Мерсена Формула ФермаФормула ВудаллаФормула Куллена
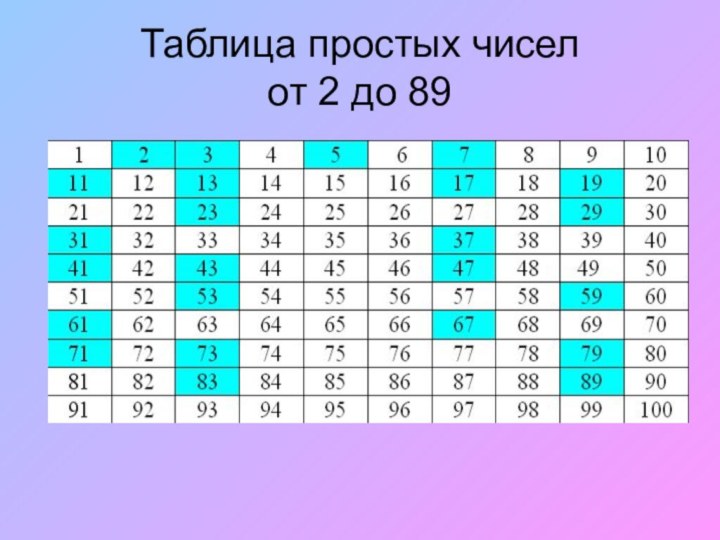
- 8. Таблица простых чисел от 2 до
- 9. Таблица простых чисел от 2 до 89
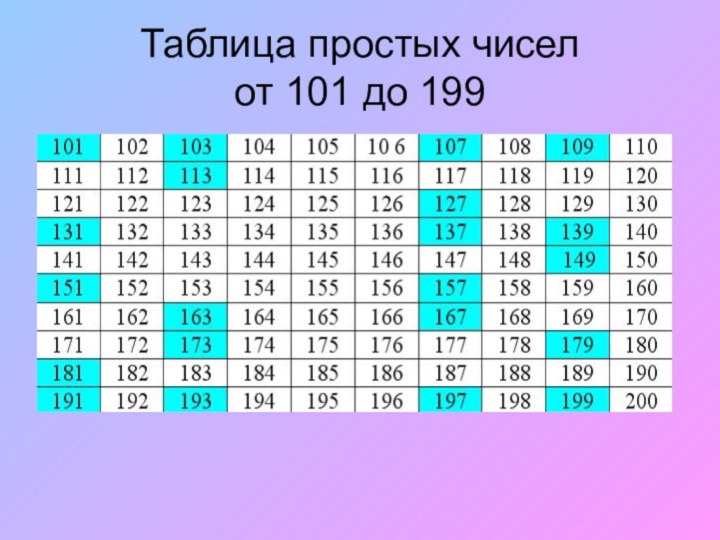
- 10. Таблица простых чисел от 101 до 199
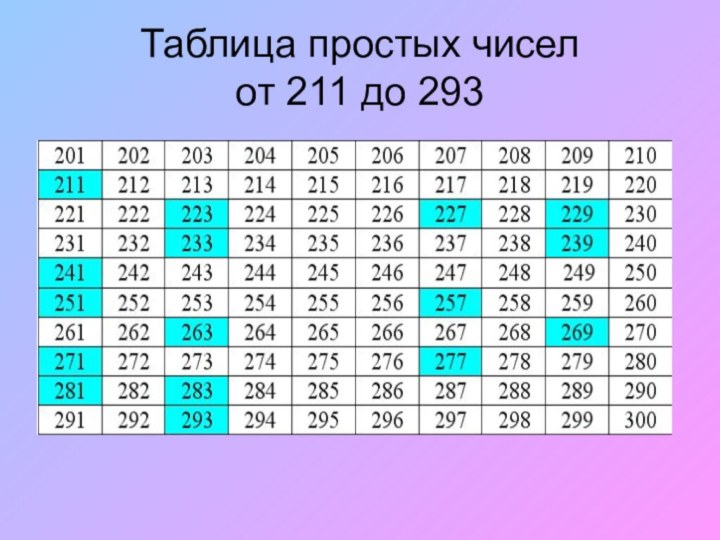
- 11. Таблица простых чисел от 211 до 293
- 12. Скатерть УламаВ зависимости от расположения натуральных чисел
- 13. Скатерть Улама
- 14. Скатерть Улама
- 16. Формула МерсеннаМ = 2р – 1, р
- 17. Формула ФермаF = 22n + 1, n
- 18. Формула ВудаллаW = n2n – 1, n
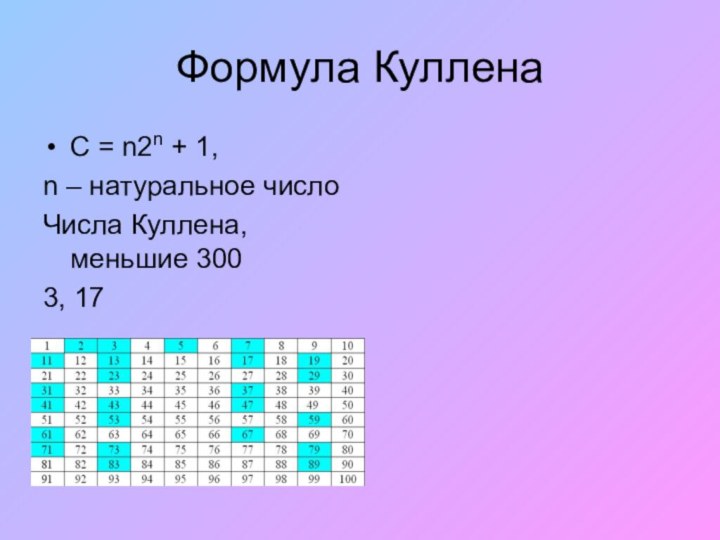
- 19. Формула КулленаC = n2n + 1, n – натуральное числоЧисла Куллена, меньшие 3003, 17
- 20. ВыводНа данный момент известны различные способы получения
- 21. Скачать презентацию
- 22. Похожие презентации
Цель работыСоставить таблицу простых чисел от 1 до 300 разными способами и дать оценку этим способам













Слайд 2
Цель работы
Составить таблицу простых чисел от 1 до
300 разными способами и дать оценку этим способам
Слайд 3
Задачи работы
Изучить тему «Простые числа»;
Найти в научной литературе
и на образовательных сайтах сети Internet формулы для получения
простых чисел;применить найденные способы для получения простых чисел от 1 до 300;
Сделать вывод по проделанной работе.
Слайд 4
Определение простых чисел
Натуральное число p называется простым, если
оно имеет ровно два делителя 1 и р.
Примеры простых
чисел: 2,131, 659 …
Слайд 5
Где применяются простые числа?
В математике простые числа применяются
для приведения дробей к общему знаменателю, для сокращения дробей,
при решении уравнений;В криптографии для шифрования данных;
В математическом моделировании.
Слайд 7
Как получить простые числа?
Решето Эратосфена
Скатерть Улама
Формула Мерсена
Формула Ферма
Формула Вудалла
Формула Куллена
Слайд 8
Таблица простых чисел
от 2 до 89
Впишем в
таблицe 10 х10 все натуральные числа последовательно от 1
до 100. Прежде всего, надо «выбросить» все четные числа, кроме 2. Подчеркнув число 2, остальные числа, делящиеся на 2, зачеркнем. После 2 в таблице идет простое число 3. Подчеркнем число 3 как простое, а все остальные, делящееся на 3, зачеркнем. Теперь следующее простое число 5, которое опять подчеркиваем и выбрасываем все числа, кратные 5, и т. д. Заметим, что из всех натуральных чисел не зачеркнутыми остаются простые числа. Эратосфен у каждого составного числа прокладывал отверстие, и получалось нечто вроде решета, через которое эти составные числа «просеивались».
Слайд 12
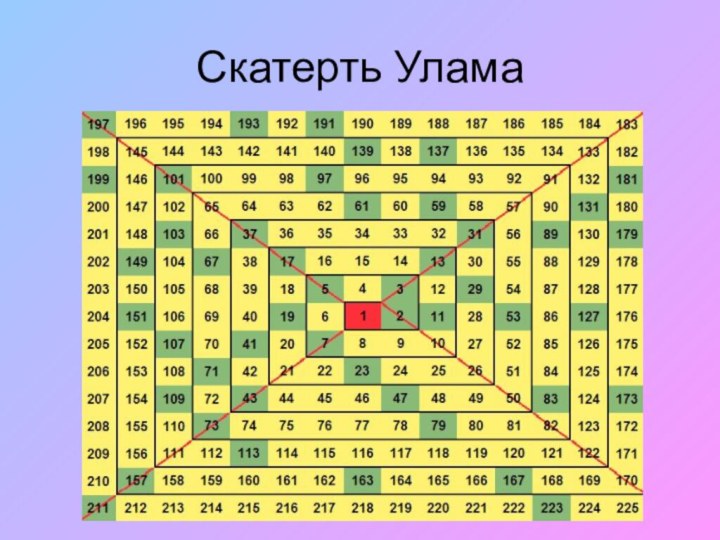
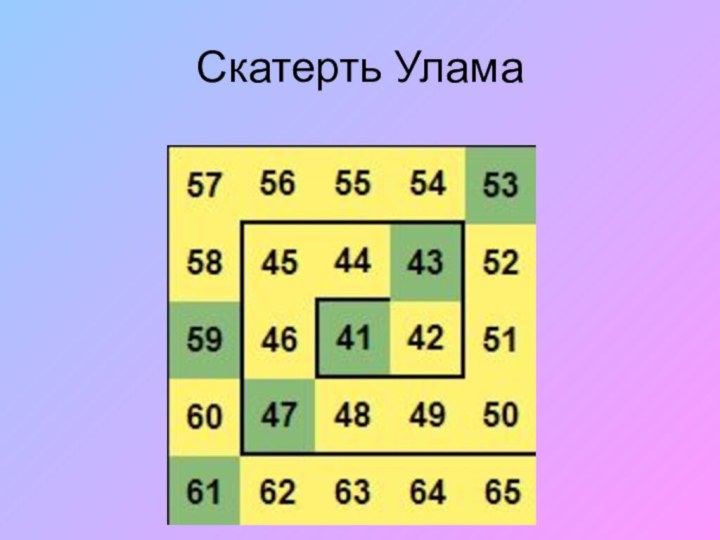
Скатерть Улама
В зависимости от расположения натуральных чисел простые
числа могут образовывать тот или иной узор. Однажды математику
Станиславу М. Уламу пришло в голову идея расположить натуральные числа по спирали начиная с 1. Легко заметить, что простые числа расположены по диагональным линиям.
Слайд 16
Формула Мерсенна
М = 2р – 1,
р –
простое число
Числа Мерсенна меньшие 300
3,7,31,127
французский монах Мерен Мерсенн
1588-1648
один
из основателей Парижской Академии наук самое большое простое число (2009 г) имеет
12 978 189 десятичных цифр и является простым числом Мерсенна
Слайд 17
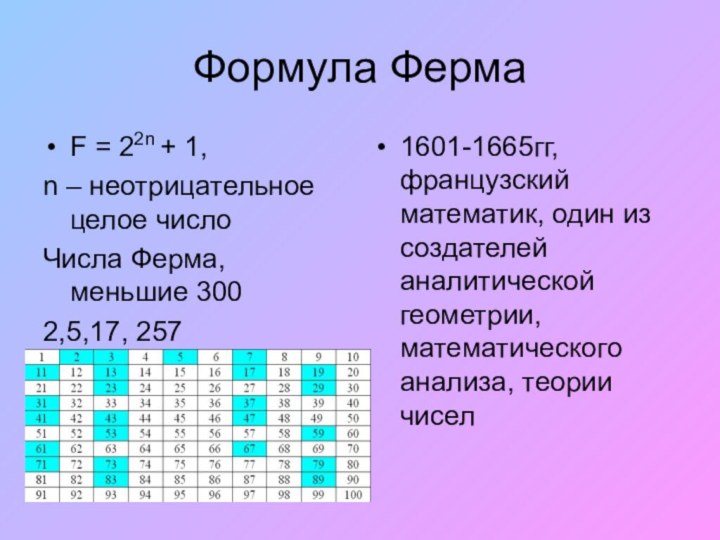
Формула Ферма
F = 22n + 1,
n –
неотрицательное целое число
Числа Ферма, меньшие 300
2,5,17, 257
1601-1665гг, французский математик,
один из создателей аналитической геометрии, математического анализа, теории чисел
Слайд 18
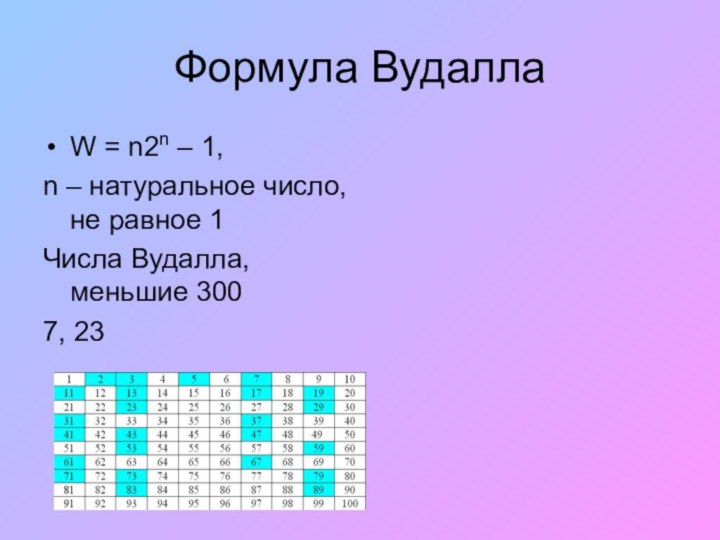
Формула Вудалла
W = n2n – 1,
n –
натуральное число, не равное 1
Числа Вудалла, меньшие 300
7, 23
Слайд 20
Вывод
На данный момент известны различные способы получения простых
чисел. Выполняя работу я заметила, что по данным формулам
вычисляются не все простые числа в выбранном промежутке от 1 до 300.Все простые числа по порядку получаются тогда, когда мы применяем Решето Эратосфена.