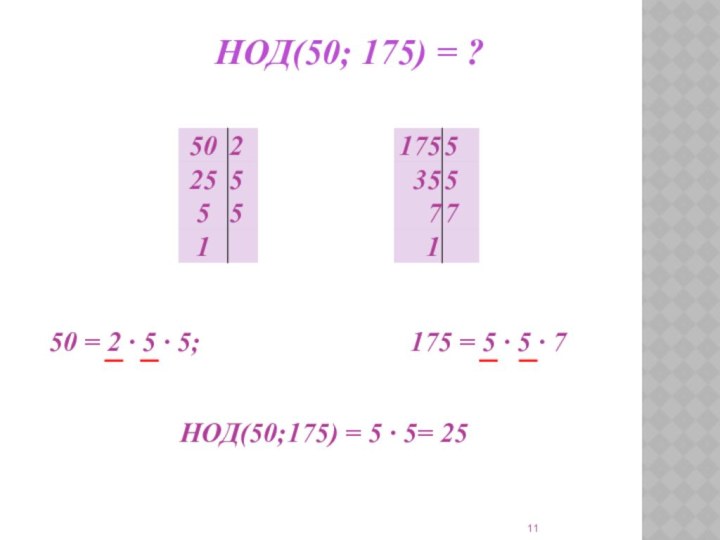
наибольшего общего делителя;
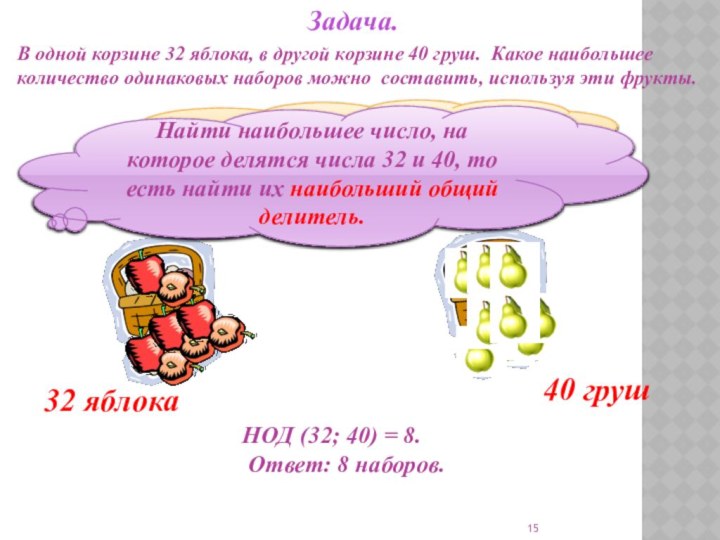
отрабатывать умение решать задачи на использование
НОД чисел; обобщить имеющиеся у учащихся знания о наибольшем общем делителе натуральных чисел, о взаимно простых числах.