Слайд 2
Цель урока:
познакомить учащихся с правилом нахождения последней
цифры результата без вычислений примера;
развивать умение работать с
натуральными, четными и нечетными числами, последовательностями;
развивать интерес к математике, коммуникативную, информационно-познавательную, социально-трудовую компетентности.
Слайд 3
Подготовка к уроку:
Разделить класс на четыре команды; приготовить
карточки и наглядные пособия для проведения таймов; турнирную таблицу.
Ход
проведения занятия:
Игра проводится в 4 тайма по 5 минут. Между таймами – перерывы (5 минут).
Время перерывов – это время, когда тренер дает рекомендации своей команде с помощью которых можно одержать победу. В игре матбол во время перерывов учитель будет давать немного новой информации, которую учащиеся могут использовать при выполнении заданий – это и будут рекомендации тренера.
Каждый тайм раздаются задания на карточках, на их выполнение отводится ровно 5 минут. После чего проверяются решения и ответы заданий и расставляются заработанные очки. Задания одинаковые, проверка происходит у доски.
Слайд 4
1 тайм
Представьте первые десять чисел натурального ряда, используя:
пять раз цифру 2 и известные арифметические действия:
22222=1
22222=2
3.
22222=3
4. 22222=4
5. 22222=5
6. 22222=6
7. 22222=7
8. 22222=8
22222=9
22222=10
Вот задача не для робких!
Вычитай. Дели и множь,
Плюсы ставь, а так же скобки!
Верим, к финишу придешь!
Слайд 5
Перерыв:
1. Продолжить ряд:
2; 6; 12; 20; 30; 42;…
1; 3; 9; 27; 81;…
2. Заполните свободную клетку:
Слайд 6
Ответы:
1) Первый ряд создается с помощью увеличения на
последовательные четные числа: 4, 6, 8, 10 и так
далее, поэтому после числа 40 будет находиться число 56 = 42 + 14.
Второй ряд создан с помощью умножения на число 3, поэтому после числа 81 будет располагаться число 243 = 81 ∙ 3.
2) Сначала проверяются все результаты всех действий между крайними числами, если ответы не подходят, то выполняются действия с цифрами данных чисел:
84: 8 + 4 = 12; 16: 1 + 6 = 7; 19 = 12 + 7
53: 5 + 3 = 8; 21: 2 + 1 = 3; 11 = 8 + 3
41: 4 + 1 = 5; 37: 3 + 7 = 10; 5 + 10 = 15
Слайд 7
2 тайм
Продолжить предложенные ряды еще двумя числами.
1) 2;
3; 6; 7; 10; 11; 14;…
2) 9; 8; 11;
10; 13; 12;…
3) 1; 1; 2; 3; 5; 8;…
4) 7; 14; 10; 2; 4; 8;16;…
5) 1; 2; 6; 24;…
Слайд 8
Перерыв
Когда два числа складываются в
столбик, последняя цифра суммы зависит только от последних цифр
слагаемых, а остальные их цифры на нее никак не влияют. Точно так же при вычитании и умножении последняя цифра результата зависит только от последних цифр данных чисел.
Слайд 9
Перерыв
Поэтому при нахождении последних цифр
сложного числового выражения, составленного из сумм и произведений, многозначные
числа можно заменять их последними цифрами. Например, для нахождения последней цифры данного примера проводятся следующие действия:
243 ∙ 682 + 4731 ∙ 6946 + 374 ∙ 693 ∙ 485
Слайд 10
Перерыв продолжается…
Для этого сначала найдем последние цифры каждого
из произведений. Получим 6, 6 и 0. Сумма 6
+ 6 + 0 оканчивается цифрой 2, значит, последняя цифра первоначальной суммы также 2.
Если в выражении имеется разность, то решение немного усложняется. Например, действуя таким же образом, мы получили бы, что последняя цифра выражения
5871 ∙ 741 + 8403 ∙ 4118 – 653 ∙ 111 ∙ 61673
есть 1 + 4 – 9, что невозможно. Но наше рассуждение можно подправить: последняя цифра первого слагаемого та же самая, что у числа 11, и поэтому последняя цифра у заданного «большого числа» та же самая, что и у 11 + 4 – 9, то есть 6.
Гораздо сложнее обстоит дело с определением последней цифры частного, это будет изучаться позднее.
Слайд 11
3 тайм
Определить последнюю цифру (не равную нулю) для
следующих выражений:
1) 34 ∙ 728 + 71 ∙ 957
+ 649 ∙ 752 ∙ 16;
2) 76 ∙ 382 – 58 ∙ 333 + 88 ∙ 1991;
3) сумма всех однозначных чисел;
4) сумма всех двузначных чисел;
5) в произведении первых двадцати натуральных чисел.
Слайд 12
Перерыв
m -- натуральное
число
m – четное число, если m делится на 2
m
– нечетное число, если m не делится на 2
Слайд 13
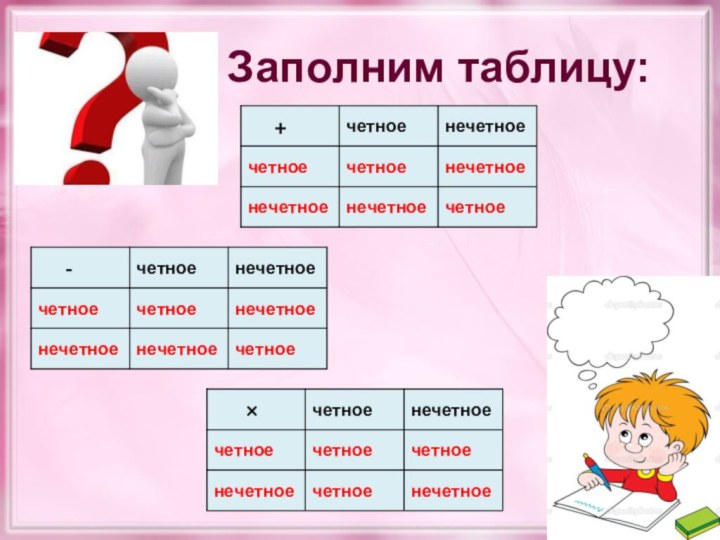
Запомни!!!
Четное + четное = четное;
Нечетное + нечетное =
четное;
Четное + нечетное = нечетное;
Нечетное +… + нечетное =
четное;
количество слагаемых четно
5. Нечетное +… + нечетное = нечетное
количество слагаемых нечетно
6. Четное число + 1 = нечетное
Слайд 15
Игра: « Кто выбрал четное число».
Даны два числа

– одно четное, другое нечетное, и предложено двум лицам
взять одному четное число, а другому – нечетное, как кто пожелает. Угадать, кто выбрал четное число, а кто нечетное, не составит труда.
Предлагается, например Мише и Маши два числа: 2 (которое является четным) и 3 (нечетное). Миша и Маша сами между собой делят эти два числа, у кого какое – никто не знает.
Чтобы отгадать, у кого из них какое число, предлагается Мише умножить свое число на четное число – 10, а Маше умножить на 5, которое является нечетным. После этого результаты складываются, и сумма произносится в слух. От того, каким числом будет сумма: четным или нечетным числом.
Если сумма число четное – это значит, что у Миши нечетное число, то есть 3, а у Маши – четное: 2. Это происходит потому, что сумма может быть четной только в том случае, если оба слагаемых или четные числа, или нечетные. Оба нечетными они быть не могут, следовательно: оба полученные слагаемые у Маши и Миши – четные числа. Чтобы произведение было четным, а до сложения ученики умножали свои числа, один из множитель должен быть четным. У числа 3 был сомножитель – 10, а у числа 2 – оставшийся множитель 5.
Если же сумма получилась числом нечетным, значит у Миши четное число – 2, а у Маши нечетное число – 3. Тогда Машино слагаемое получается числом нечетным, а от туда и нечетная сумма.
Слайд 16
4 ТАЙМ
Определите четным или нечетным числом является:
1) сумма
всех натуральных чисел от 1 до 100;
2) сумма всех
нечетных чисел от 1 до 49;
3) произведение двух последовательных натуральных чисел;
4) произведение однозначных чисел.
5) Что можно сказать о двух числах, если известно, что их сумма
Слайд 17
Происходит подсчет баллов, распределяются места, награждаются победители и
не только.