Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему Лог-линейный анализ

Содержание

2. ЦелиЧто делать, если таблица сопряженности не двухмерная, а трехмерная или еще хуже?
3. Применять лог-линейный анализ!
4. МОДЕЛИМатематики любят модели.Каждая модель соответствует определенной гипотезе о переменных, входящих в таблицу сопряженности.
5. МОДЕЛИИдея состоит в том, чтобы взять модель
6. МОДЕЛИВ модели лог-линейного анализа переменные НЕ ДЕЛЯТСЯ на независимые и зависимые переменные!
7. ДВУХМЕРНАЯ МОДЕЛЬРассмотрим сначала лог-линейную модель для двухмерной
8. ДВУХМЕРНАЯ МОДЕЛЬ✵ Наблюдаемое значение – это эмпирическая
9. ДВУХМЕРНАЯ МОДЕЛЬ✵ Наблюдаемое значение – это эмпирическая
10. ДВУХМЕРНАЯ МОДЕЛЬПредположив, что наблюдения независимы, получаем:pi. –
11. Помните, как мы определяли теоретическую частоту?Для выделенной
12. ДВУХМЕРНАЯ МОДЕЛЬВозьмем натуральный логарифм и получим:
13. ДВУХМЕРНАЯ МОДЕЛЬА это выражение можно представить в виде:где
14. ДВУХМЕРНАЯ МОДЕЛЬ✵ говорят, что u представляет собой
15. ДВУХМЕРНАЯ МОДЕЛЬЗначения, представленные как главные эффекты в
16. ДВУХМЕРНАЯ МОДЕЛЬЛог-линейная модель может быть проверена посредством
17. ДВУХМЕРНАЯ МОДЕЛЬЕсли модель с независимыми переменными плохо
18. ДВУХМЕРНАЯ МОДЕЛЬЭта модель всегда полностью описывает таблицу сопряженности размером 2*2. ln Fij=u+u1(i)+u2(j)+u12(ij)
19. ТРЕХМЕРНАЯ МОДЕЛЬu – общий «средний» эффектu1 –
20. ТРЕХМЕРНАЯ МОДЕЛЬЦЕЛЬ:найти модель с минимальным количеством параметров, которая бы адекватно предсказывала эмпирические частоты
21. ТРЕХМЕРНАЯ МОДЕЛЬСледует помнить, что данная модель –
22. ТРЕХМЕРНАЯ МОДЕЛЬНапример, если слагаемое u123 включено, то
23. ТРЕХМЕРНАЯ МОДЕЛЬКаждая модель, которую можно придумать для
24. Любимый примерУсложним любимый пример: пусть теперь мы
25. Модель (1)(1) ln Fij=u Все частоты в таблице одинаковы
26. Модель (2) [1](2) ln Fij=u+u1 Маргинальные частоты для переменных 2 и 3 равны
27. Модель (3) [1] [2](3) ln Fij=u+u1+u2 Маргинальные частоты для переменной 3 равны
28. Эти модели являются неинтересными, так как не
29. Модель (4) [1] [2] [3](4) ln Fij=u+u1+u2+u3Все переменные независимы (?)
30. Модель (5) [12] [3](5) ln Fij=u+u1+u2+u3+u12
31. Модель (5) [12] [3]Все дети любят кошек,
32. Модель (6) [12] [13](6) ln Fij=u+u1+u2+u3+u12+u13
33. Модель (6) [12] [13] Возраст и
34. Модель (7) [12] [13] [23](7) ln Fij=u+u1+u2+u3+u12+u13+u23Каждая
35. Модель (7) [12] [13] [23]Женщины любят собак,
36. Модель (8) [123](8) ln Fij=u+u1+u2+u3+u12+u13+u23+u123 Взаимодействие второго порядка.Все переменные связаны.
37. Модель (8) [123]Маленькие мальчики любят кошек, а
38. Больше для трехмерного случая никаких моделей придумать нельзя. СЛАВА БОГУ!
39. Лог-линейные модели можно подбирать для четырех и более переменных аналогичным образом
40. ✵ Главная идея метода:
41. Эти ценные сведения о лог-линейном анализе
42. А нам теперь интересно, как найти подходящую модель, если у нас есть только данные.
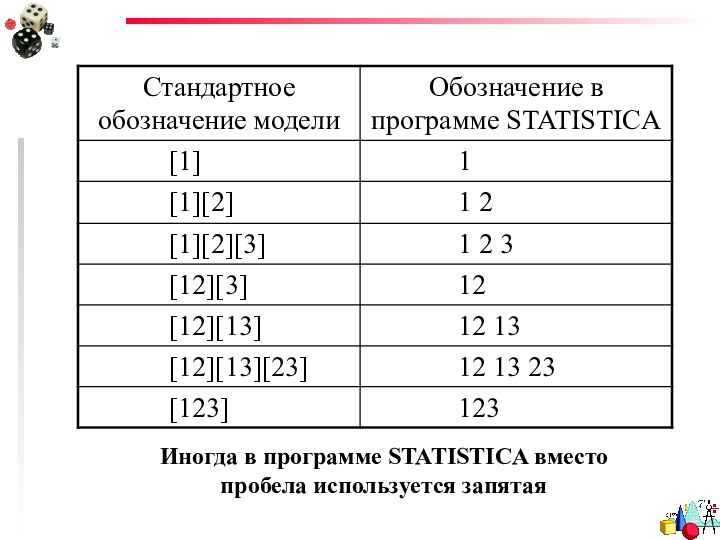
43. Это можно сделать в программе STATISTICA, в
44. Иногда в программе STATISTICA вместо пробела используется запятая
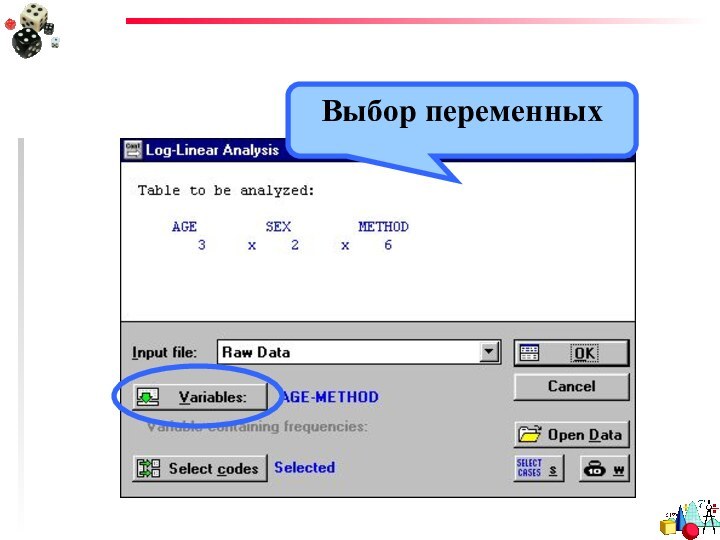
45. Выбор переменных
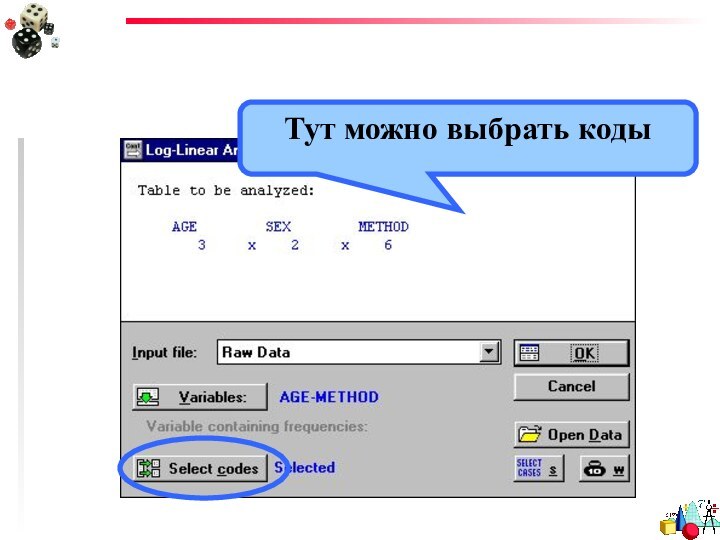
46. Тут можно выбрать коды
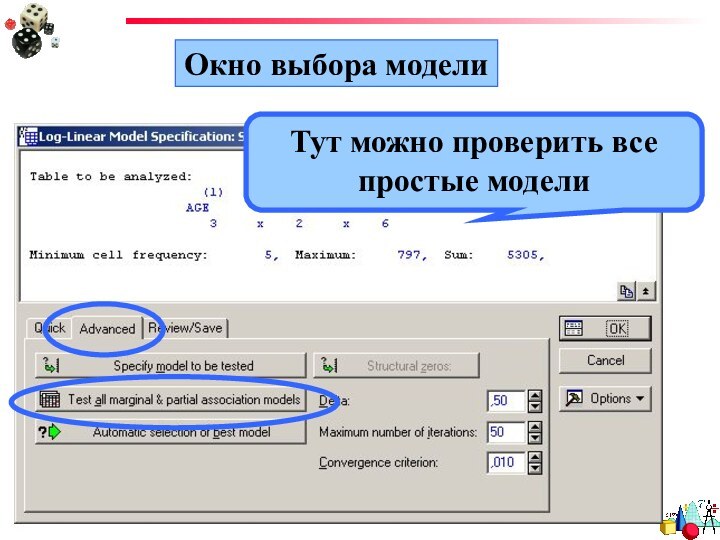
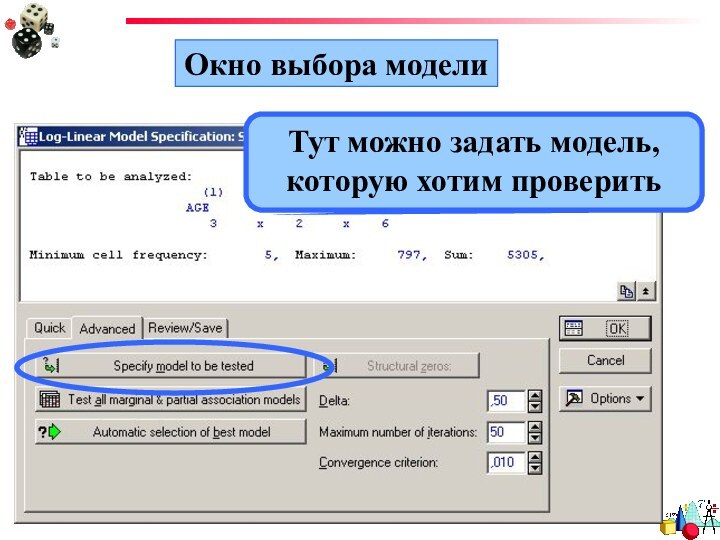
47. Окно выбора моделиТут можно проверить все простые модели
48. Окно выбора моделиТут можно задать модель, которую хотим проверить
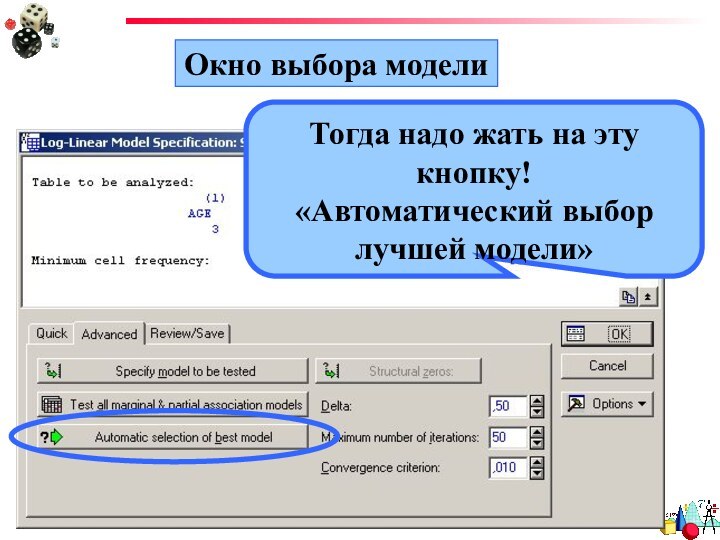
49. Какой ужас!А если я забыл, как обозначаются модели?!!Или совсем не помню, какие модели бывают?!!
50. Окно выбора моделиТогда надо жать на эту кнопку!«Автоматический выбор лучшей модели»
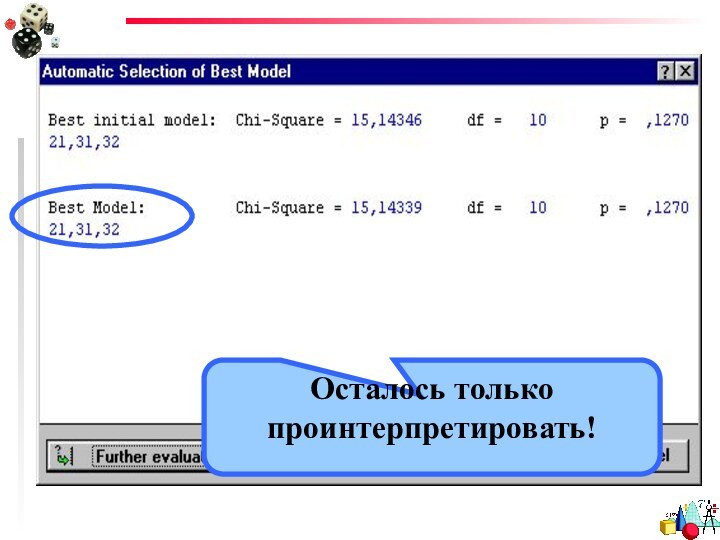
51. Осталось только проинтерпретировать!
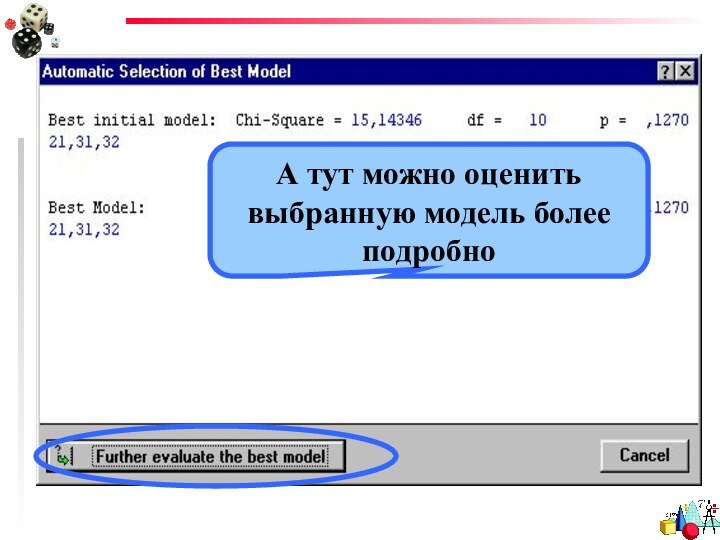
52. А тут можно оценить выбранную модель более подробно
53. Скачать презентацию
54. Похожие презентации

ЦелиЧто делать, если таблица сопряженности не двухмерная, а трехмерная или еще хуже?

Лог-линейный анализCтат. методы в психологии(Радчикова Н.П.)

МОДЕЛИМатематики любят модели.Каждая модель соответствует определенной гипотезе о переменных, входящих в таблицу сопряженности.

МОДЕЛИИдея состоит в том, чтобы взять модель и проверить, совпадают ли эмпирические

МОДЕЛИВ модели лог-линейного анализа переменные НЕ ДЕЛЯТСЯ на независимые и зависимые переменные!

ДВУХМЕРНАЯ МОДЕЛЬРассмотрим сначала лог-линейную модель для двухмерной таблицы сопряженности с r строками

ДВУХМЕРНАЯ МОДЕЛЬ✵ Наблюдаемое значение – это эмпирическая частота nij в каждой клетке

ДВУХМЕРНАЯ МОДЕЛЬПредположив, что наблюдения независимы, получаем:pi. – это вероятность попасть в категорию

Помните, как мы определяли теоретическую частоту?Для выделенной ячейки:Вероятность оказаться мужчиной равна 200/550,

ДВУХМЕРНАЯ МОДЕЛЬВозьмем натуральный логарифм и получим:

ДВУХМЕРНАЯ МОДЕЛЬА это выражение можно представить в виде:где

ДВУХМЕРНАЯ МОДЕЛЬ✵ говорят, что u представляет собой «общий средний эффект» ✵ u1(i)

ДВУХМЕРНАЯ МОДЕЛЬЗначения, представленные как главные эффекты в этой модели, просто отражают разницу

ДВУХМЕРНАЯ МОДЕЛЬЛог-линейная модель может быть проверена посредством оценки параметров (т.е. теоретических частот)

ДВУХМЕРНАЯ МОДЕЛЬЕсли модель с независимыми переменными плохо подходит для оценки исходной таблицы

ДВУХМЕРНАЯ МОДЕЛЬЭта модель всегда полностью описывает таблицу сопряженности размером 2*2. ln Fij=u+u1(i)+u2(j)+u12(ij)

ТРЕХМЕРНАЯ МОДЕЛЬu – общий «средний» эффектu1 – главный эффект переменной 1u2 –

ТРЕХМЕРНАЯ МОДЕЛЬЦЕЛЬ:найти модель с минимальным количеством параметров, которая бы адекватно предсказывала эмпирические частоты

ТРЕХМЕРНАЯ МОДЕЛЬСледует помнить, что данная модель – иерархическая. Это значит, что если в

ТРЕХМЕРНАЯ МОДЕЛЬНапример, если слагаемое u123 включено, то будут включены и слагаемые u1,

ТРЕХМЕРНАЯ МОДЕЛЬКаждая модель, которую можно придумать для трехмерной таблицы сопряженности, соответствует определенной

Любимый примерУсложним любимый пример: пусть теперь мы хотим проверить, правда ли, что

Модель (1)(1) ln Fij=u Все частоты в таблице одинаковы

Модель (2) [1](2) ln Fij=u+u1 Маргинальные частоты для переменных 2 и 3 равны

Модель (3) [1] [2](3) ln Fij=u+u1+u2 Маргинальные частоты для переменной 3 равны

Эти модели являются неинтересными, так как не позволяют эмпирическим частотам отражать эмпирическую

Модель (4) [1] [2] [3](4) ln Fij=u+u1+u2+u3Все переменные независимы (?)

Модель (5) [12] [3](5) ln Fij=u+u1+u2+u3+u12 Переменные 1 и 2

Модель (5) [12] [3]Все дети любят кошек, а взрослые – собак.Переменные «возраст»

Модель (6) [12] [13](6) ln Fij=u+u1+u2+u3+u12+u13 Переменные 2 и 3 независимы

Модель (6) [12] [13] Возраст и предпочтение домашнего животного связаны с

Модель (7) [12] [13] [23](7) ln Fij=u+u1+u2+u3+u12+u13+u23Каждая пара переменных связана, но направление

Модель (7) [12] [13] [23]Женщины любят собак, а мужчины кошек.Дети любят кошек,

Модель (8) [123](8) ln Fij=u+u1+u2+u3+u12+u13+u23+u123 Взаимодействие второго порядка.Все переменные связаны.

Модель (8) [123]Маленькие мальчики любят кошек, а взрослые мужчины – собак. Маленькие

Больше для трехмерного случая никаких моделей придумать нельзя. СЛАВА БОГУ!

Лог-линейные модели можно подбирать для четырех и более переменных аналогичным образом

✵ Главная идея метода: Подбираем последовательно модели

Эти ценные сведения о лог-линейном анализе можно почерпнуть вEveritt B.S. Making

А нам теперь интересно, как найти подходящую модель, если у нас есть только данные.

Это можно сделать в программе STATISTICA, в специальном модулеStatistics - Advanced Linear/Nonlinear

Иногда в программе STATISTICA вместо пробела используется запятая

Окно выбора моделиТут можно проверить все простые модели

Окно выбора моделиТут можно задать модель, которую хотим проверить

Какой ужас!А если я забыл, как обозначаются модели?!!Или совсем не помню, какие модели бывают?!!

Окно выбора моделиТогда надо жать на эту кнопку!«Автоматический выбор лучшей модели»

А тут можно оценить выбранную модель более подробно

Ура! Я могу посчитать лог-линейный анализ!

Слайды презентации

Слайд 2 Цели
Что делать, если таблица сопряженности не двухмерная, а

трехмерная или еще хуже?

Слайд 3
Применять лог-линейный анализ!

Слайд 4 МОДЕЛИ
Математики любят модели.
Каждая модель соответствует определенной гипотезе о

переменных, входящих в таблицу сопряженности.

Слайд 5 МОДЕЛИ
Идея состоит в том, чтобы взять модель и

МОДЕЛИИдея состоит в том, чтобы взять модель и проверить, совпадают ли

проверить, совпадают ли эмпирические данные с предсказанными моделью результатами.
Та

модель , где совпадение наибольшее, признается лучшей, т.е. наиболее адекватно описывающей полученные данные.

Слайд 6 МОДЕЛИ
В модели лог-линейного анализа переменные
НЕ ДЕЛЯТСЯ
на

независимые и зависимые переменные
!

Слайд 7 ДВУХМЕРНАЯ МОДЕЛЬ
Рассмотрим сначала лог-линейную модель для двухмерной таблицы

ДВУХМЕРНАЯ МОДЕЛЬРассмотрим сначала лог-линейную модель для двухмерной таблицы сопряженности с r

сопряженности с r строками и с столбцами
Наблюдаемое значение =

ожидаемое значение + ошибка

Слайд 8 ДВУХМЕРНАЯ МОДЕЛЬ
✵ Наблюдаемое значение – это эмпирическая частота

ДВУХМЕРНАЯ МОДЕЛЬ✵ Наблюдаемое значение – это эмпирическая частота nij в каждой

nij в каждой клетке таблицы
✵Ожидаемое значение – это

теоретическая частота Fij

Поэтому можно написать:

nij = Fij + ошибка

Слайд 9 ДВУХМЕРНАЯ МОДЕЛЬ
✵ Наблюдаемое значение – это эмпирическая частота

nij в каждой клетке таблицы
✵Ожидаемое значение – это

теоретическая частота Fij

Поэтому можно написать:

nij = Fij + ошибка

Слайд 10 ДВУХМЕРНАЯ МОДЕЛЬ
Предположив, что наблюдения независимы, получаем:

pi. – это

ДВУХМЕРНАЯ МОДЕЛЬПредположив, что наблюдения независимы, получаем:pi. – это вероятность попасть в

вероятность попасть в категорию i переменной 1,

p.j – это вероятность попасть в категорию j переменной 2.

Слайд 11 Помните, как мы определяли теоретическую частоту?
Для выделенной ячейки:

Вероятность

Помните, как мы определяли теоретическую частоту?Для выделенной ячейки:Вероятность оказаться мужчиной равна

оказаться мужчиной равна 200/550, т.е. Fi.=200

Вероятность предпочитать собак равна

350/550, т.е. F.j=350

Подставив все это в формулу

получим теоретическую частоту для выделенной клетки:
Fij=(200/550 )*(350/550)*550=127,3.

Слайд 12 ДВУХМЕРНАЯ МОДЕЛЬ
Возьмем натуральный логарифм и получим:

Слайд 13 ДВУХМЕРНАЯ МОДЕЛЬ
А это выражение можно представить в виде:

где

Слайд 14 ДВУХМЕРНАЯ МОДЕЛЬ
✵ говорят, что u представляет
собой «общий

ДВУХМЕРНАЯ МОДЕЛЬ✵ говорят, что u представляет собой «общий средний эффект» ✵

средний эффект»
✵ u1(i) - «главный эффект» уровня i

переменной , расположенной по строкам
✵ u2(j) - «главный эффект» уровня j переменной , расположенной по столбцам

Слайд 15 ДВУХМЕРНАЯ МОДЕЛЬ
Значения, представленные как главные эффекты в этой

ДВУХМЕРНАЯ МОДЕЛЬЗначения, представленные как главные эффекты в этой модели, просто отражают

модели, просто отражают разницу между маргинальными частотами по строкам

или столбцам и мало нас интересуют

Слайд 16 ДВУХМЕРНАЯ МОДЕЛЬ
Лог-линейная модель может быть проверена посредством оценки

ДВУХМЕРНАЯ МОДЕЛЬЛог-линейная модель может быть проверена посредством оценки параметров (т.е. теоретических

параметров (т.е. теоретических частот) и сравнением этих оценок с

наблюдаемыми (эмпирическими) частотами. Это можно сделать с помощью известной нам процедуры
χ2 Пирсона

Слайд 17 ДВУХМЕРНАЯ МОДЕЛЬ
Если модель с независимыми переменными плохо подходит

ДВУХМЕРНАЯ МОДЕЛЬЕсли модель с независимыми переменными плохо подходит для оценки исходной

для оценки исходной таблицы (т.е. χ2 получился значимый), то

в модель следует ввести дополнительной слагаемое, которое будет представлять собой связь между переменными

ln Fij=u+u1(i)+u2(j)+u12(ij)

Слайд 18 ДВУХМЕРНАЯ МОДЕЛЬ
Эта модель всегда полностью описывает
таблицу сопряженности

размером 2*2.

ln Fij=u+u1(i)+u2(j)+u12(ij)

Слайд 19 ТРЕХМЕРНАЯ МОДЕЛЬ
u – общий «средний» эффект
u1 – главный

эффект переменной 1
u2 – главный эффект переменной 2
u3– главный

эффект переменной 3
u12– взаимодействие между переменными 1 и 2
u13 – взаимодействие между переменными 1 и 3 u23 – взаимодействие между переменными 3 и 2 u123 – взаимодействие между тремя переменными (взаимодействие второго порядка)

ln Fij=u+u1+u2+u3+u12+u13+u23+u123

Слайд 20 ТРЕХМЕРНАЯ МОДЕЛЬ
ЦЕЛЬ:
найти модель с минимальным количеством параметров, которая

бы адекватно предсказывала эмпирические частоты

Слайд 21 ТРЕХМЕРНАЯ МОДЕЛЬ
Следует помнить,
что данная модель – иерархическая.

Это

ТРЕХМЕРНАЯ МОДЕЛЬСледует помнить, что данная модель – иерархическая. Это значит, что если

значит, что если в модель включены эффекты более высоких

порядков, то автоматически включаются и эффекты более низких порядков.

Слайд 22 ТРЕХМЕРНАЯ МОДЕЛЬ
Например, если слагаемое u123 включено, то будут

ТРЕХМЕРНАЯ МОДЕЛЬНапример, если слагаемое u123 включено, то будут включены и слагаемые

включены и слагаемые u1, u2, u3, u12, u13 и

u23 .

Например, модель

ln Fij=u+u2+u3+u123

недопустима.

Слайд 23 ТРЕХМЕРНАЯ МОДЕЛЬ
Каждая модель, которую можно придумать для трехмерной

ТРЕХМЕРНАЯ МОДЕЛЬКаждая модель, которую можно придумать для трехмерной таблицы сопряженности, соответствует

таблицы сопряженности, соответствует определенной гипотезе о переменных, входящих в

таблицу.

Рассмотрим каждую модель подробнее.

Слайд 24 Любимый пример
Усложним любимый пример: пусть теперь мы хотим

Любимый примерУсложним любимый пример: пусть теперь мы хотим проверить, правда ли,

проверить, правда ли, что мужчины больше любят собак, а

женщины – кошек, и не зависит ли это отношение от возраста

Слайд 25 Модель (1)
(1) ln Fij=u
Все частоты

в таблице одинаковы

Слайд 26 Модель (2) [1]
(2) ln Fij=u+u1
Маргинальные частоты

для переменных 2 и 3
равны

Слайд 27 Модель (3) [1] [2]
(3) ln Fij=u+u1+u2

Маргинальные частоты для переменной
3 равны

Слайд 28 Эти модели являются неинтересными, так как не позволяют

Эти модели являются неинтересными, так как не позволяют эмпирическим частотам отражать

эмпирическим частотам отражать эмпирическую разницу в маргинальных частотах каждой

переменной. Фактически они сводятся к двухмерному случаю.

И, видимо, могут быть проинтерпретированы как случай, когда все три переменные независимы.

Слайд 29 Модель (4) [1] [2] [3]
(4) ln Fij=u+u1+u2+u3
Все переменные

независимы (?)

Слайд 30 Модель (5) [12] [3]
(5) ln Fij=u+u1+u2+u3+u12

Переменные 1 и 2 зависимы и обе

независимы от переменной 3.

Слайд 31 Модель (5) [12] [3]
Все дети любят кошек, а

Модель (5) [12] [3]Все дети любят кошек, а взрослые – собак.Переменные

взрослые – собак.
Переменные «возраст» и «домашнее животное» связаны, и

обе они не зависят от пола.

Слайд 32 Модель (6) [12] [13]
(6) ln Fij=u+u1+u2+u3+u12+u13

Переменные

2 и 3 независимы на каждом уровне переменной 1,

но каждая зависит от переменной 1.

Слайд 33 Модель (6) [12] [13]
Возраст и предпочтение

домашнего животного связаны с полом, но возраст и предпочтение

домашнего животного не связаны.

Слайд 34 Модель (7) [12] [13] [23]
(7) ln Fij=u+u1+u2+u3+u12+u13+u23
Каждая пара

Модель (7) [12] [13] [23](7) ln Fij=u+u1+u2+u3+u12+u13+u23Каждая пара переменных связана, но

переменных связана, но направление связи одинаково для каждого уровня

третьей переменной.

Слайд 35 Модель (7) [12] [13] [23]
Женщины любят собак, а

Модель (7) [12] [13] [23]Женщины любят собак, а мужчины кошек.Дети любят

мужчины кошек.
Дети любят кошек, а взрослые собак.
Женщины взрослые, а

мужчины – дети.

Слайд 36 Модель (8) [123]
(8) ln Fij=u+u1+u2+u3+u12+u13+u23+u123

Взаимодействие второго

порядка.
Все переменные связаны.

Слайд 37 Модель (8) [123]
Маленькие мальчики любят кошек, а взрослые

Модель (8) [123]Маленькие мальчики любят кошек, а взрослые мужчины – собак.

мужчины – собак. Маленькие девочки любят собак, а взрослые

женщины – кошек.

Слайд 38 Больше для трехмерного случая никаких моделей придумать нельзя.

СЛАВА

БОГУ!

Слайд 39 Лог-линейные модели можно подбирать для четырех и более

переменных аналогичным образом

Слайд 40
✵ Главная идея метода:
Подбираем

✵ Главная идея метода: Подбираем последовательно модели от

последовательно модели
от самых простых до самых

сложных и проверяем, насколько
предсказанные моделью частоты
совпадают с эмпирическими
частотами.
Если совпадают, процесс подбора
модели закончен.
Поэтому удачной будет та модель, для
которой хи-квадрат незначимый!