Презентация на тему Задачи с экономическим содержанием 2

по вкладам (депозитам).
2. познакомиться с дифференцированные (неравными) платежами и

с аннуитетными (равными) платежами.

именно о задачах по математике, а не по экономике.

Вообще говоря, любую задачу, условие которой связано с товарно-денежными отношениями, производством товаров и услуг, минимизацией расходов или максимизацией прибыли и т. п., можно отнести к задачам с экономическим содержанием. Подобные задачи встречаются на самых разных позициях в вариантах ЕГЭ по математике—от первых до последних.
Сегодня мы рассмотрим следующие задачи:
• задачи о кредитовании и банковских процентах.

на банковские проценты можно условно разделить на две группы:

Задачи на проценты по вкладам (депозитам),
Задачи о кредитах.

не високосном году клиент открыл вклад в банке1 сентября

сроком на 1 месяц под 12% годовых. Сколько рублей окажется на счёте вклада 1 октября того же года, если сумма вклада равна
100 000 рублей?

Какой вклад выгоднее: первый—на 1 год под 13% годовых,

или второй—на 3 месяца (с автоматической пролонгацией каждые три месяца в течение года) под 12% годовых? При расчётах считайте, что один месяц равен
1/12 части года.

− 2) +…+ 1 легко вычисляется по формуле

банке кредит сроком на 4 года под 16% годовых.

На сколько процентов сумма всех выплат банку окажется больше суммы кредита, если досрочное погашение кредита не предполагается?

Пример 4.
Иван планирует взять ипотечный

кредит (кредит на покупку квартиры под залог квартиры) в банке на несколько лет под 10% годовых на следующих условиях: по истечении каждого года пользования кредитом он должен возвращать банку часть кредита, равную сумме кредита, делённой на число лет пользования кредитом (погашать кредит), и выплачивать банковские проценты за пользование кредитом в размере 10% от не погашенной к моменту очередного платежа суммы кредита. Так, если кредит взят на 5 лет, то за первый год пользования кредитом Иван должен выплатить пятую часть суммы кредита и 10% от всей суммы кредита, за второй год пятую часть суммы кредита и 10% от непогашенной суммы кредита, т. е. oт 4/5 суммы кредита, и т. п. При оформлении кредита банк предложил Ивану выплачивать кредит ежемесячными равными платежами по следующей схеме: сумма кредита и сумма процентов за всё время пользования кредитом суммируются и делятся на число месяцев пользования кредитом. Иван принял предложение банка. Известно, что сумма ежемесячного платежа равна 30 000 рублей, а сумма начисленных процентов оказалась равна сумме кредита.
а) На сколько лет был взят кредит?
б) Чему равна сумма кредита (в рублях)?

Как видим, эта задача оказалась типичной задачей на кредит с дифференцированными платежами по упрощённой схеме. Отметим, что её формулировка не слишком удачна в части условий кредитования, и у некоторых экзаменуемых трудности в решении могут быть обусловлены лингвистикой, а не математикой: ведь в задаче не указано, часть какого долга (первоначального или с начисленными процентами) берётся для расчёта выплат. Более удачными формулировками соответствующих условий возврата кредита являются следующие:
• 1-го числа каждого месяца на ещё не выплаченную часть кредита начисляется r%, т. е. к ещё не выплаченной части кредита добавляется r% от этой части;
• со 2-го по 14-е число каждого месяца необходимо выплатить 1/19 часть долга и проценты, начисленные 1-го числа этого месяца.
Тем не менее, внимательное чтение и анализ условия задачи позволяют правильно интерпретировать его и получить нужный результат; в этом смысле задача является корректной.

1 июля не високосного года Екатерина

взяла в банке
кредит на сумму 109 500 рублей под 24% годовых сроком на 6 месяцев на условиях погашения кредита дифференцированными платежами. Это означает, что до 1 числа каждого следующего за июлем месяца она вносит в банк платёж, состоящий из 1/6
части долга (т. е. 18 250 рублей) и процентов, которые начисляются с учётом числа
дней соответствующего месяца: 30 или 31 (всего 6 платежей). Найдите сумму всех выплат по кредиту..

в банке кредит на сумму 109 500 рублей под

24% годовых сроком на 6 месяцев на условиях погашения кредита ежемесячными равными (аннуитетными) платежами. Это означает, что
• до истечения соответствующего платёжного периода, т. е. до 1-го числа каждого следующего за июлем месяца, банк начисляет 24% на оставшуюся сумму долга, т. е. увеличивает её на 24%;
• после начисления процентов Екатерина вносит в банк (также до истечения соответствующего платёжного периода, т. е. до 1-го числа каждого месяца начиная с августа) некоторую фиксированную сумму—одну и ту же для каждого платежа; сумма долга при этом уменьшается, и на эту уменьшенную сумму начисляются проценты до истечения следующего платёжного периода, после чего Екатерина вносит в банк платёж в размере той же фиксированной суммы, и т. п.
Найдите сумму всех выплат по кредиту.

по математике обычно рассматриваются несколько упрощённые схемы, например, кредит

выдаётся на условиях оплаты тремя равными платежами с начислением фиксированного про- цента на сумму долга за каждый период.

Пример 7. 31 декабря 2014 года бизнесмен взял в банке кредит на 3 года под 10% годовых. Схема выплаты кредита следующая: до 31 ноября каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т. е. увеличивает долг на 10%), затем до истеченияэтого же платёжного периода (т. е. по 31 декабря того же года) бизнесмен переводит в банк определённую (одну и ту же для каждого года) сумму ежегодного платежа. Какой была сумма кредита (в рублях), если сумма ежегодного платежа составила 2 662 000 рублей?

используются формулы, связывающие 4 величины: сумму кредита, процентную ставку,

число платежей (срок кредита), сумму регулярного платежа. Обычно в условии задания ЕГЭ задаются три из этих величин, а четвёртую требуется найти.
Так, в рассмотренном примере были заданы процентная ставка, число
платежей, сумма регулярного платежа, а требовалось найти сумму
кредита.

Пример 8. В июле планируется взять кредит в банке на сумму
4,5 млн рублей на срок 9 лет. Условия его возврата таковы:
• каждый январь долг возрастает на r% по сравнению с концом
предыдущего года;
• с февраля по июнь каждого года необходимо выплатить часть долга;
• в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Найдите r, если известно, что наибольший годовой платёж по кредиту составит не более 1,4 млн рублей, а наименьший—не менее
0,6 млн рублей.

рублей) по состоянию на июль должен уменьшаться до нуля

равномерно, т. е. на 1/9часть, поэтому суммы долга за каждый год (до начисления процентов)составят (в порядке убывания)4,5, 4, …, 1, 0,5.
По условию каждый январь долг возрастает на r%. поэтому последовательность размеров платежей по процентам будет следующей:
4,5 ・r/100, 4 ・r/100, …, 0,5 ・r/100.
Ежемесячный платёж состоит из фиксированной суммы 4,5/9= 0,5 и суммы платежа по процентам. Следовательно, наибольший платёж составит 0,5 +4,5 ・r/100 млн рублей, а наименьший платёж составит 0,5+0,5 ・r/100 млн рублей.
Получаем 0,5+4,5 ・r/100 ≤1,4, откуда r≤20, и 0,5+0,5 ・r/100 ≥ 0,6, откуда r≥20. Следовательно, r=20.
Ответ. 20.

не используя формулы, а ограничившись простым перебором (оформлять который

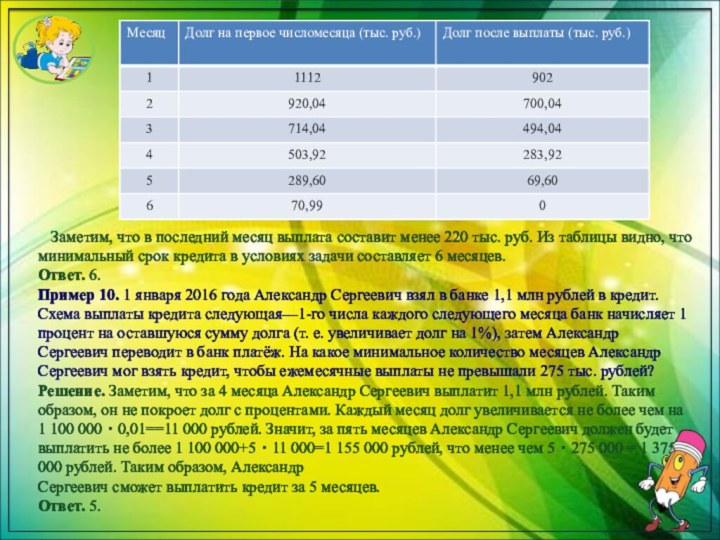
для наглядности лучше с помощью таблицы) или элементарными логическими построениями. Рассмотрим оба этих способа на примере двух аналогичных заданий.

Пример 9. 1 января 2016 года Тарас Павлович взял в банке 1,1 млн рублей в кредит. Схема выплаты кредита следующая—1-го числа каждого следующего месяца банк начисляет 2 процента на оставшуюся сумму долга (т. е. увеличивает долг на 2%), затем Тарас Павлович переводит в банк платёж. На какое минимальное количество месяцев Тарас Павлович мог взять кредит, чтобы ежемесячные выплаты не превышали 220 тыс. рублей?

Решение. Ясно, что чем больше месячные выплаты, тем быстрее будет выплачен долг. Значит, срок кредита будет минимален в том случае, когда величина выплаты будет равна 220 тыс. рублей. Составим таблицу, в первом столбце которой будем указывать долг на первое число месяца, а во втором—долг в том же месяце, но уже после выплаты. Для упрощения расчётов будем сохранять только два знака после запятой, представляя суммы долга в тыс. рублей.

составит менее 220 тыс. руб. Из таблицы видно, что

минимальный срок кредита в условиях задачи составляет 6 месяцев.
Ответ. 6.
Пример 10. 1 января 2016 года Александр Сергеевич взял в банке 1,1 млн рублей в кредит. Схема выплаты кредита следующая—1-го числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (т. е. увеличивает долг на 1%), затем Александр Сергеевич переводит в банк платёж. На какое минимальное количество месяцев Александр Сергеевич мог взять кредит, чтобы ежемесячные выплаты не превышали 275 тыс. рублей?
Решение. Заметим, что за 4 месяца Александр Сергеевич выплатит 1,1 млн рублей. Таким образом, он не покроет долг с процентами. Каждый месяц долг увеличивается не более чем на 1 100 000 ・ 0,01==11 000 рублей. Значит, за пять месяцев Александр Сергеевич должен будет выплатить не более 1 100 000+5 ・ 11 000=1 155 000 рублей, что менее чем 5 ・ 275 000 = 1 375 000 рублей. Таким образом, Александр
Сергеевич сможет выплатить кредит за 5 месяцев.
Ответ. 5.