- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Понятие логарифма
Содержание
- 2. 8. Найдите xЗадание № 1 (устно).
- 3. Проверка:1) x = 32) x = -2/33) Корней нет6) ?4) x₁‚₂= ±23Задание № 2.Решите уравнения:3
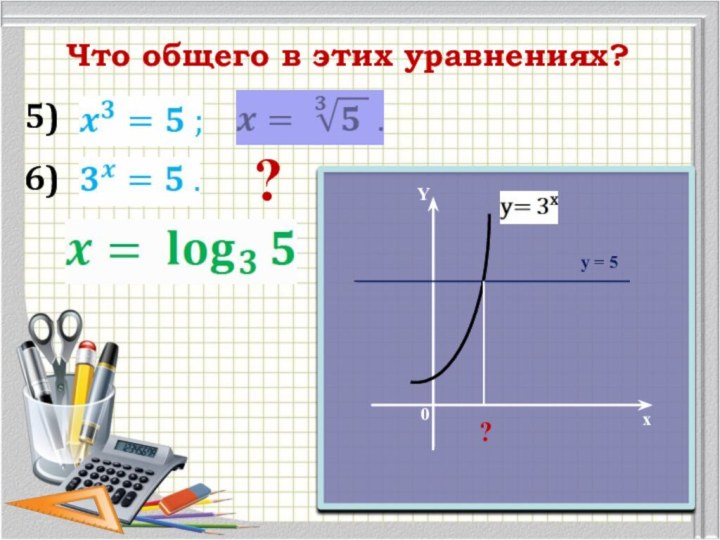
- 4. Что общего в этих уравнениях?5) 6) ?Yx0y = 5?
- 6. Логарифмом положительного числа b по положительному и
- 7. Например:так кактак кактак кактак как
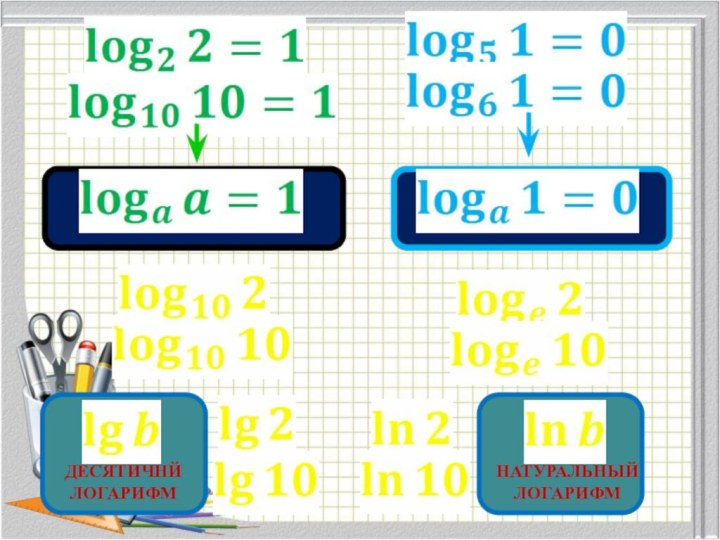
- 8. ДЕСЯТИЧНЙ ЛОГАРИФМНАТУРАЛЬНЫЙ ЛОГАРИФМ
- 9. Log 2 16;
- 10. Сравните со своими ответами !Log 2 16;
- 11. подставимОсновное логарифмическое тождество
- 12. Самостоятельная работаПриложение: задание №4-5
- 13. Для чего были придуманы логарифмы ? Как
- 14. …Если необходимость совершать обратную операцию к операции
- 15. Джон Непер(1550-1617) – английский математик. Изобретатель логарифмов,
- 16. Современное определение логарифма появилось у Леонарда Эйлера
- 17. Скачать презентацию
- 18. Похожие презентации
8. Найдите xЗадание № 1 (устно).















Слайд 6
Логарифмом положительного числа b по положительному и отличному
от 1 основанию a называется
показатель степени,
в которую нужно
возвести число a, чтобы получить число b.b > 0,
a > 0,
a ≠ 1.
Слайд 9 Log 2 16;
log 2 64;
log 2 2;Log 2 1 ; log 2 (1/2); log 2 (1/8);
Log 3 27; log 3 81; log 3 3;
Log 3 1; log 3 (1/9); log 3 (1/3);
Log1/2 1/32; log1/2 4; log0,5 0,125;
Log0/5 (1/2); log0,5 1; log1/2 2.
Задание №3. Вычислите:
Слайд 10
Сравните со своими ответами !
Log 2 16;
log 2 64;
log 2 2;Log 2 1 ; log 2 (1/2); log 2 (1/8);
Log 3 27; log 3 81; log 3 3;
Log 3 1; log 3 (1/9); log 3 (1/3);
Log1/2 1/32; log1/2 4; log0,5 0,125;
Log0,5 (1/2); log0,5 1; log1/2 2.
Таблица ответов:
Слайд 13
Для чего были придуманы логарифмы ?
Как сказал французский
математик
П. Лаплас,
«изобретение логарифмов, сократив работу астрономов,
продлило им жизнь». Слайд 14 …Если необходимость совершать обратную операцию к операции возведения
в n-ую степень, была осознана достаточно давно, то задача
нахождения показателя степени по заданному результату, т. е. задача решения уравнения стала интересной лишь в XVII веке.Для чего были придуманы логарифмы ?





























