- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Свойства параллельных прямых
Содержание
- 2. Цели урока:Рассмотреть свойства параллельных прямых;Показать применение свойств
- 3. Решите задачу (рис.1)А) Доказать: АВ // СD.Б) Дано: АВ // СD.Найти: ∟ЕКС. АBCD3030ЕКА)рис.1АCЕBКDБ)30?
- 4. ЗАДАЧА. Пусть а // b,
- 5. Свойство накрест лежащих углов при параллельных прямых
- 6. В чем заключается разница между этими теоремами?1122Прямые
- 7. Следствие Если прямая перпендикулярна к одной из
- 8. Свойство соответственных углов при параллельных прямых и
- 9. Решение задач по готовым чертежамДано:∟1=75, а //
- 10. Домашнее задание: п.29. вопросы 12-151) Дано:
- 11. Скачать презентацию
- 12. Похожие презентации





Слайд 2
Цели урока:
Рассмотреть свойства параллельных прямых;
Показать применение свойств параллельных
прямых;
задач.
Слайд 3
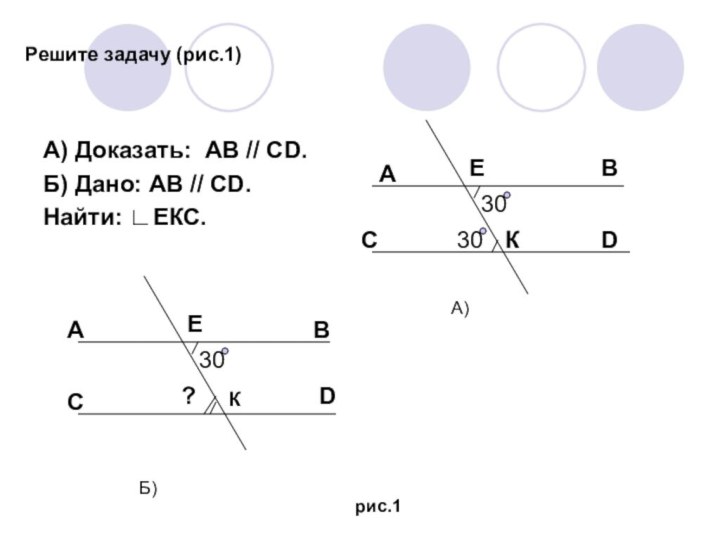
Решите задачу (рис.1)
А) Доказать: АВ // СD.
Б) Дано:
АВ // СD.
Найти: ∟ЕКС.
А
B
C
D
30
30
Е
К
А)
рис.1
А
C
Е
B
К
D
Б)
30
?
Слайд 4 ЗАДАЧА. Пусть а // b, с
– их секущая, ∟1 и ∟2 – накрест лежащие
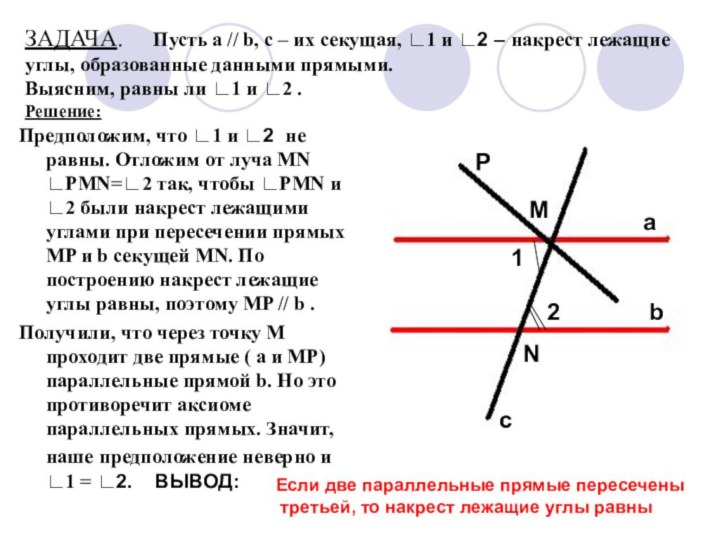
углы, образованные данными прямыми. Выясним, равны ли ∟1 и ∟2 . Решение:Предположим, что ∟1 и ∟2 не равны. Отложим от луча МN ∟PMN=∟2 так, чтобы ∟PMN и ∟2 были накрест лежащими углами при пересечении прямых MP и b секущей MN. По построению накрест лежащие углы равны, поэтому MP // b .
Получили, что через точку М проходит две прямые ( а и MP) параллельные прямой b. Но это противоречит аксиоме параллельных прямых. Значит, наше предположение неверно и ∟1 = ∟2. ВЫВОД:
Р
М
N
а
b
с
1
2
Если две параллельные прямые пересечены
третьей, то накрест лежащие углы равны
Слайд 5 Свойство накрест лежащих углов при параллельных прямых и
их секущей
Если две параллельные прямые пересечены секущей, то накрест
лежащие углы равныОбратная теорема
Это такая теорема, в которой условием является заключение данной теоремы, а заключением –условие данной теоремы
Метод доказательства от противного
Метод, в котором предполагается противоположное тому, что нужно доказать.
Слайд 6
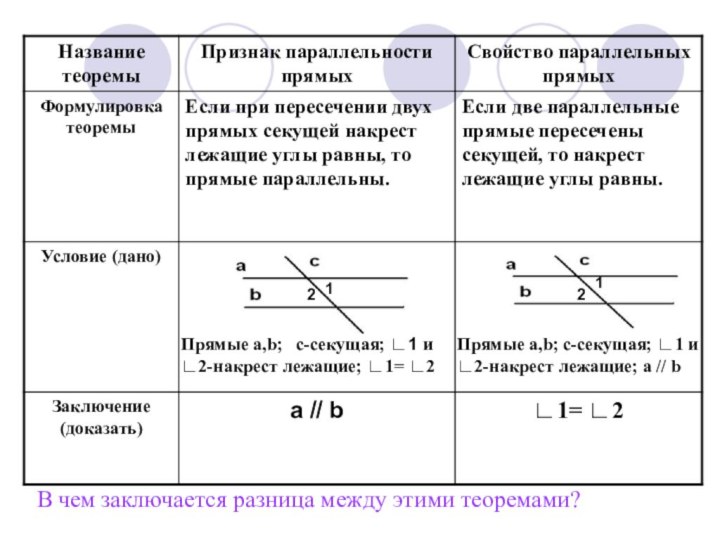
В чем заключается разница между этими теоремами?
1
1
2
2
Прямые a,b;
c-секущая; ∟1 и ∟2-накрест лежащие; ∟1= ∟2
Прямые a,b;
c-секущая; ∟1 и ∟2-накрест лежащие; а // b
Слайд 7
Следствие
Если прямая перпендикулярна к одной из двух
параллельных прямых, то она перпендикулярна и к другой .
1
2
Дано:
а // b, с а, т.е. ∟ 1=90.Доказать: с b.
Доказательство:
Прямая с пересекает прямую а, поэтому она пересекает также прямую b. При пересечении параллельных прямых а и b секущей с образуются равные накрест лежащие углы: ∟1= ∟2. Так как ∟1= 90, то и ∟2 = 90, т.е. с b, ч.т.д.
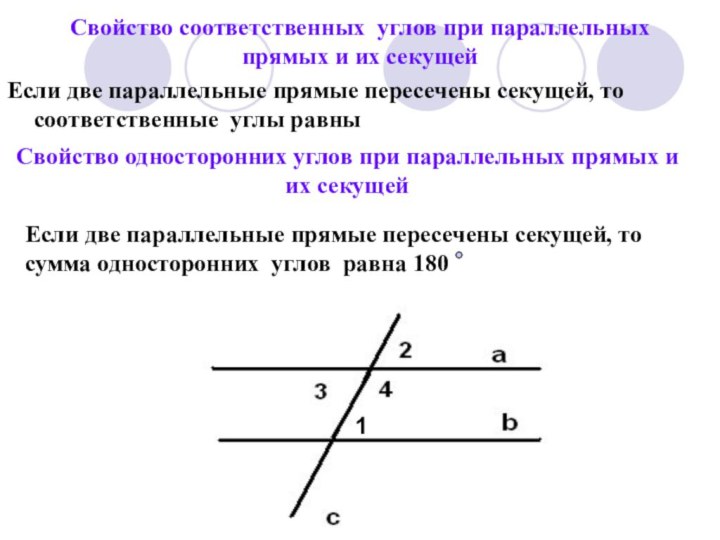
Слайд 8 Свойство соответственных углов при параллельных прямых и их
секущей
Если две параллельные прямые пересечены секущей, то соответственные углы
равныСвойство односторонних углов при параллельных прямых и их секущей
Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180
1
Слайд 9
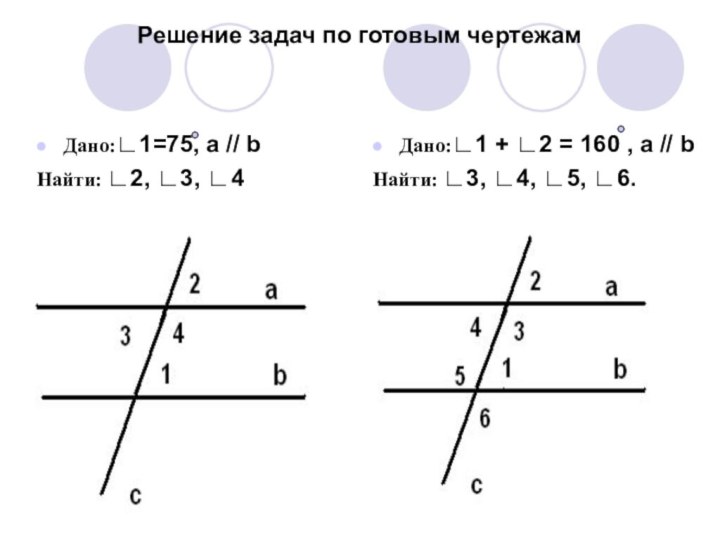
Решение задач по готовым чертежам
Дано:∟1=75, а // b
Найти:
∟2, ∟3, ∟4
Дано:∟1 + ∟2 = 160 , а
// bНайти: ∟3, ∟4, ∟5, ∟6.
Слайд 10
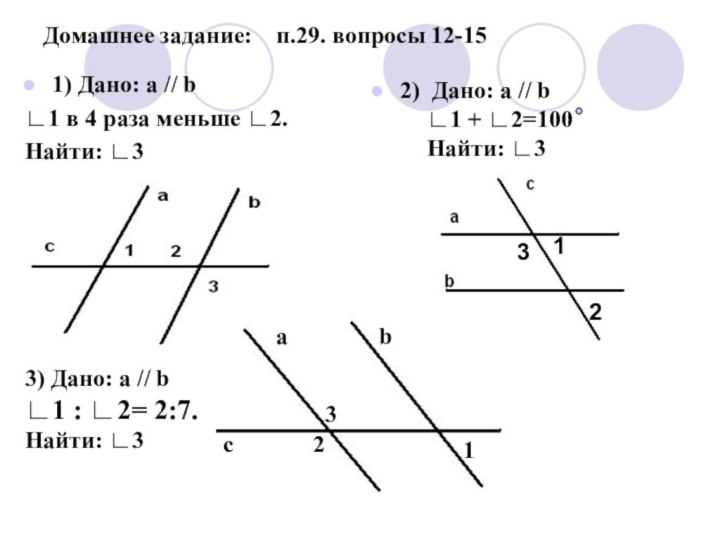
Домашнее задание: п.29. вопросы 12-15
1) Дано: а
// b
∟1 в 4 раза меньше ∟2.
Найти: ∟3
2)
Дано: а // b∟1 + ∟2=100
Найти: ∟3
3
1
2
3) Дано: а // b
∟1 : ∟2= 2:7.
Найти: ∟3
а
b
с
3
2
1