Слайд 2
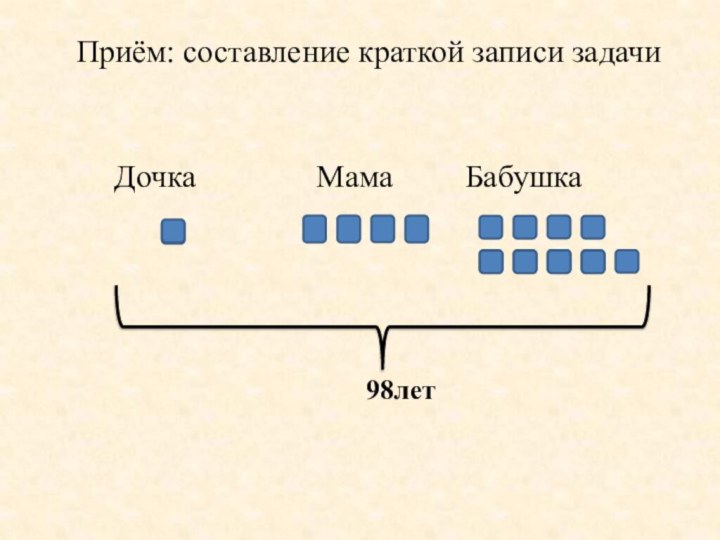
Приём: составление краткой записи задачи
Дочка
Слайд 3
Приём: составление краткой записи задачи
Виноград содержит 90% влаги,
а изюм – 5%. Сколько килограммов винограда требуется для
получения 20 килограммов изюма?
(открытый банк заданий по математике ЕГЭ)
Слайд 4
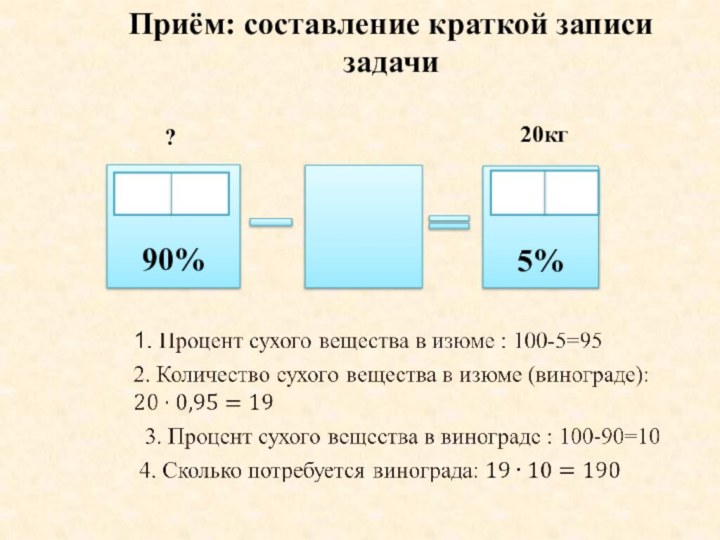
Приём: составление краткой записи задачи
90%
?
20кг
Слайд 5
Контекстные задачи
задачи, целью решения которых является разрешение
стандартной или нестандартной ситуации (предметной, межпредметной или практической по
описанному в ней содержанию) посредством нахождения соответствующего способа решения с обязательным использованием математических знаний
Слайд 6
Отличительные особенности контекстных задач
от стандартных математических
значимость (познавательная, профессиональная,
общекультурная, социальная) получаемого результата, что обеспечивает познавательную мотивацию
учащегося
условие задачи сформулировано как сюжет, ситуация или проблема, для разрешения которой необходимо использовать знания (из разных разделов основного предмета - математики, из другого предмета или из жизни) на которые нет явного указания в тексте задачи
информация и данные в задаче могут быть представлены в различной форме (рисунок, таблица, схема, диаграмма, график и т.д.), что потребует распознавания объектов
указание (явное или неявное) области применения результата, полученного при решении задачи
Слайд 8
Примеры контекстных задач
Плата за парковку машины на автостоянке
начисляется следующим образом: за первый час берётся 20 р.,
а за каждый следующий час (полный или неполный)автовладелец платит 12 р. Заполните таблицу и запишите формулу, по которой можно вычислить плату за n часов.
Сколько должен заплатить автовладелец за парковку, если он оставит автомобиль на стоянке на 20ч.40 мин.? На 10 суток?
(алгебра 9, Г.В. Дорофеев)
Слайд 9
Примеры контекстных задач
В среднем гражданин А. в дневное
время расходует 120 кВт электроэнергии в месяц, а в ночное
время — 185 кВт электроэнергии. Раньше у А. в квартире был установлен однотарифный счетчик, и всю электроэнергию он оплачивал по тарифу 2,40 руб. за кВт. Год назад А. установил двухтарифный счётчик, при этом дневной расход электроэнергии оплачивается по тарифу 2,40 руб. за кВт, а ночной расход оплачивается по тарифу 0,60 руб. за кВт.
В течение 12 месяцев режим потребления и тарифы оплаты электроэнергии не менялись. На сколько больше заплатил бы А. за этот период, если бы не поменялся счетчик? Ответ дайте в рублях.
(открытый банк заданий по математике ЕГЭ)
Слайд 10
Примеры контекстных задач
Теплоход рассчитан на 750 пассажиров и
25 членов команды. Каждая спасательная шлюпка может вместить 70
человек. Какое наименьшее число шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и всех членов команды?
(открытый банк заданий по математике ЕГЭ 2014)
Слайд 11
Принципы разработки контекстных задач
-
задание должно иметь личностную значимость для ученика, поскольку рассматривает
проблемы, которые могут возникать в обыденной жизни или связаны с будущей профессиональной деятельностью;
- контекст задачи не должен содержать подсказки, направленной на решение поставленной проблемы;
- задача может иметь несколько вариантов решения, из которых хотя бы один не отвечает условиям заданной ситуации;
- ситуация, описанная в задании, должна обеспечивать возможность комплексной проверки уровня подготовленности учащихся
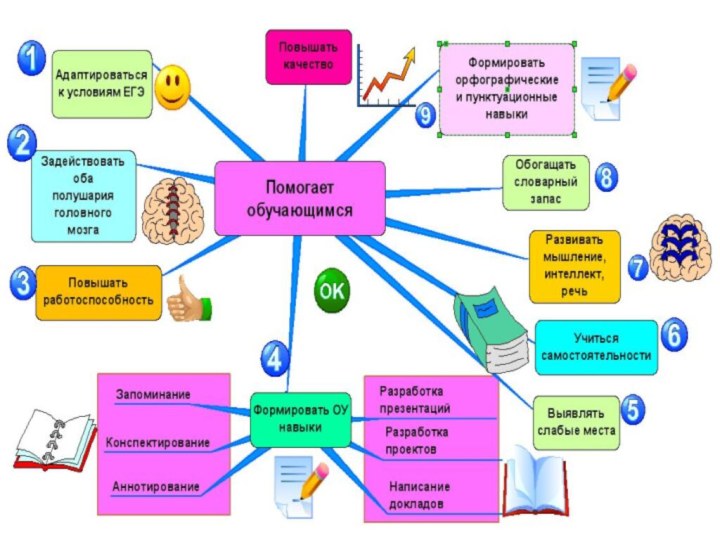
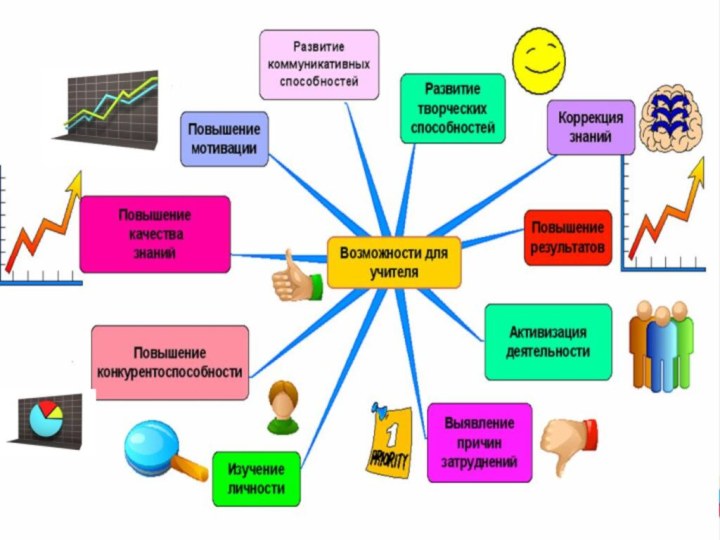
Слайд 12
Метод интеллект-карт
Свойства интеллект - карт:
Наглядность
Привлекательность
Запоминаемость
Своевременность
Творчество
Возможность пересмотра
Преимущества интеллект - карт перед другими методами:
экономия
50% времени на конспект
концентрация информации на важных моментах
визуально четкие ассоциации
улучшение запоминания
Слайд 13
Метод интеллект - карт можно использовать на разных
типах и формах урока:
изучение нового материала
закрепление материала
обобщение материала
написание доклада,
реферата, научно-исследовательской работы
подготовка проекта, презентации
конспектирование
Слайд 14
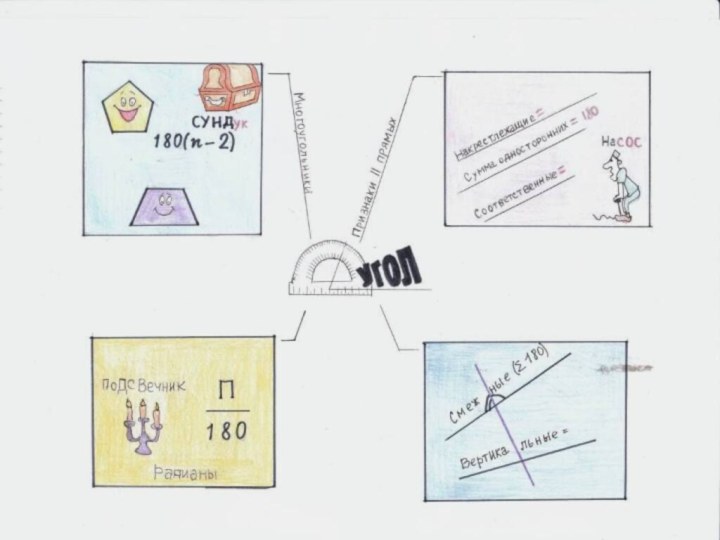
ПРАВИЛА СОЗДАНИЯ ИНТЕЛЛЕКТ-КАРТ
Для создания карт используются только цветные
карандаши, маркеры и т. д.
Основная идея, проблема или слово
располагается в центре.
Для изображения центральной идеи можно использовать рисунки, картинки. Каждая главная ветвь имеет свой цвет.
Главные ветви соединяются с центральной идеей, а ветви второго, третьего и т.д. порядка соединяются с главными ветвями.
Ветви должны быть изогнутыми, а не прямыми (как ветви дерева).
Над каждой линией – ветвью пишется только одно ключевое слово.
Для лучшего запоминания и усвоения желательно использовать рисунки, картинки, ассоциации о каждом слове.
Разросшиеся ветви можно заключать в контуры, чтобы они не смешивались с соседними ветвями
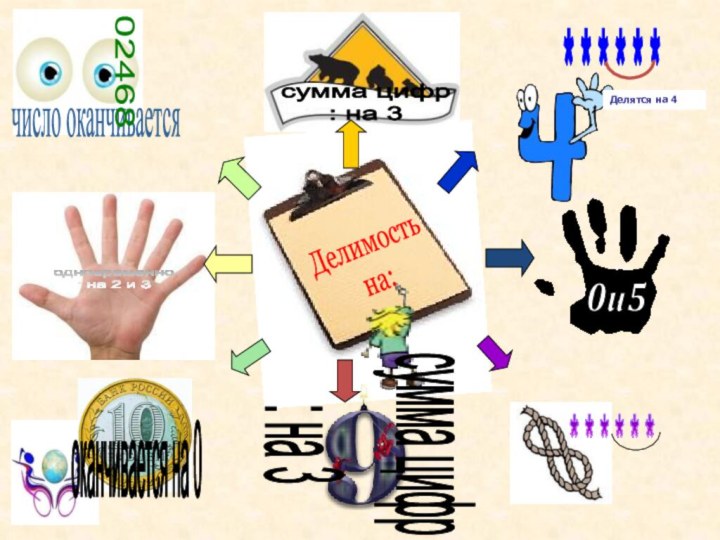
Слайд 16
Делимость
на:
0и5
число оканчивается
02468
сумма цифр
: на 3
оканчивается на 0
сумма
цифр
: на 3
* * * * * *
Делятся на
4
* * * * * *
одновременно
: на 2 и 3
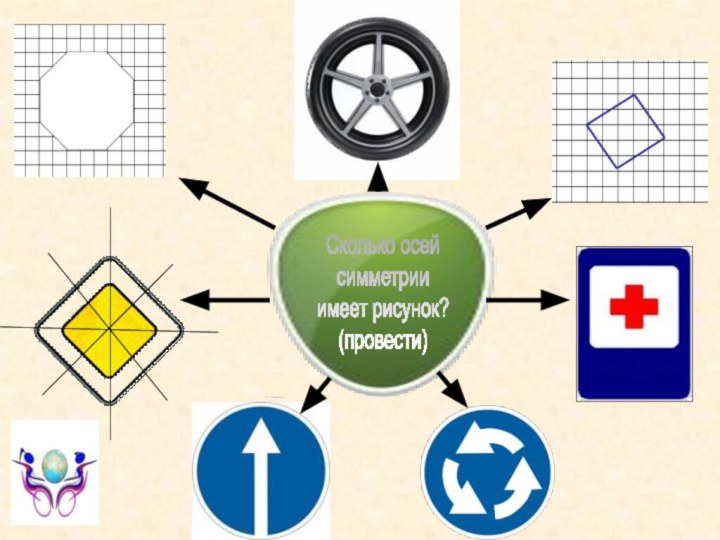
Слайд 17
Сколько осей
симметрии
имеет рисунок?
(провести)
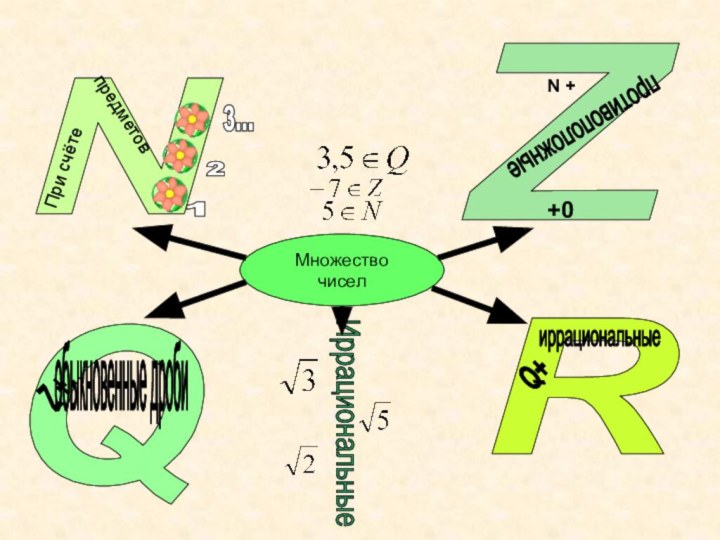
Слайд 18
Множество
чисел
N
Z
R
Q
предметов
При счёте
1
2
3...
N +
+0
противоположные
обыкновенные дроби
Z +
Иррациональные
иррациональные
Q+
Слайд 20
ПРОГРЕССИИ
Арифметическая
Геометическая
Определение:…
Определение:…
Пример…
Пример…
Формула n-ого члена…
Сумма…
Формула n-ого члена…
Сумма…
Среднее геометрическое…
Среднее арифметическое…
Слайд 23
Хороший проект должен:
иметь практическую ценность
предполагать проведение учащимися
самостоятельных исследований;
быть в одинаковой мере непредсказуемым как в
процессе работы над ним, так и при ее завершении
быть гибким в направлении работы и скорости ее выполнения
предполагать возможность решения актуальных проблем
давать учащемуся возможность учиться в соответствии с его способностями
содействовать проявлению способностей учащихся при решении задач более широкого спектра
способствовать налаживанию взаимодействия между учащимися»
Слайд 24
Темы проектов
«Старинные меры»
«Человек и координаты»
«Мир колеса»
«Ремонт
в детском саду»
«Образовательный кредит»
Преимущества технологии:
проекты позволяют ученику быть
успешным;
высокая мотивация;
связь полученных знаний с реальной жизнью;
развитие научной пытливости;
лучшая закреплённость знаний;
воспитание настойчивости в достижении цели.
Золотое сечение.ppt
Теория вероятностей.ppt
Слайд 25
Примеры здоровьесберегающей технологии
1. Упражнение выполняется стоя. Учитель произносит
или показывает аналитическую запись функции. Школьники должны изобразить руками
вид графика: например, при изучении параболы они могут изображать параболу с ветвями, направленными вверх или вниз. При изучении преобразований графиков параллельный перенос вверх показывают, вставая на цыпочки, вниз — приседая, влево и вправо — делая соответствующий поворот или шаг в нужную сторону. Растяжение и сжатие графика показывается разведением рук в стороны или сближением их
2. Предназначено для пальцев рук и является альтернативой пальчиковой гимнастике для начальных классов типа «мы писали, мы писали, наши пальчики устали». Предлагается поставить руки ладошками к учителю. Учитель читает числа. Если они делятся на - 5, то школьники сжимают ладошки в кулак, если нет — держат ладошки раскрытыми
Слайд 26
3. «Буратино» не более 3–4-х минут урока. Учащимся
предлагается закрыть глаза, представить, что нос стал, как у
Буратино, и, «обмакнув нос в чернильницу», написать, например, слово «параллелограмм». Кроме физического упражнения включается двигательная память, которая позволяет запомнить правописание математических терминов.
Гимнастика для глаз по методу Г.А.Шичко
1.Вверх-вниз, влево - вправо. Двигать глазами вверх-вниз, влево - вправо. Зажмурившись снять напряжение, считая до десяти.
2.Круг. Представьте себе большой круг. Обводите его глазами сначала по часовой стрелке, потом против часовой стрелки.
3.Квадрат. Предложить детям представить себе квадрат. Переводить взгляд из правого верхнего угла в левый нижний - в левый верхний, в правый нижний.
4.Покорчим «рожи». Учитель предлагает изображать мордочки различных животных или сказочных персонажей
Слайд 27
Мозговой штурм.docx
Обратный мозговой штурм.docx
Упражнения.docx
Принцип перехода в другое измерение.docx
Отрицание
или взгляд со стороны.docx
Переход в надсистему.docx
Переход в подсистему.docx
Слайд 28
фрейм «Солнышко»
На лучиках весёлого солнышка напишите, чему вы
сегодня на уроке научились, а на лучиках грустного –
что вам осталось непонятно, что у вас не получилось, т.е. над чем вам ещё предстоит поработать.
Слайд 29
Таким образом, современные образовательные технологии в сочетании с
современными информационными технологиями могут существенно повысить эффективность образовательного процесса,
решать стоящие перед образовательной организацией задачи воспитания всесторонне развитой, творчески свободной личности