- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему кружка по математикеМудрые науки без поучения и скуки
Содержание
- 2. Основная цель программы – развитие творческих способностей,
- 3. Достижение этой цели обеспечено посредством решения следующих
- 4. Основными педагогическими принципами, обеспечивающими реализацию программы, являются:
- 5. Математические хитрости Математические фокусыМатематические ребусы и кроссвордыМатематические игрыИнтеллект-шоуПоле чудесМатематические чудеса и тайныИ многое другое…..
- 6. Укладываем веревку с двумя петлями. На левом
- 7. Учебный курс по математике «Задачи прикладной
- 9. Задачи на расход материалов и денежных средств
- 10. 103 – тысяча106 – миллион109 – биллион
- 11. Игра-фокус.- А сейчас я буду угадывать число,
- 12. Африканская птица под арабским именем «абу-маркуб» что
- 13. Японская мудрость издревле гласит:«Великий квадрат не имеет
- 14. Ори
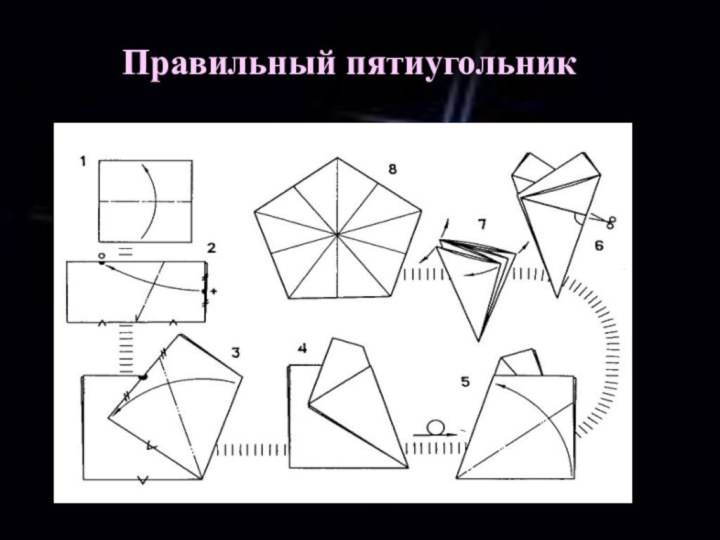
- 15. Правильный пятиугольникПравильный пятиугольник
- 16. Японский журавликИстория СадакоСхема
- 17. Оригами в математикеОчень многое в оригами связано
- 18. Да! Математику нам нужно знать!Ведь без неё
- 19. Скачать презентацию
- 20. Похожие презентации
Основная цель программы – развитие творческих способностей, логического мышления, углубление знаний, полученных на уроке, и расширение общего кругозора ребенка в процессе живого рассмотрения различных практических задач и вопросов.

















Слайд 3
Достижение этой цели обеспечено посредством решения следующих задач:
1.
Пробуждение и развитие устойчивого интереса учащихся к математике и
ее приложениям.2. Оптимальное развитие математических способностей у учащихся и привитие учащимся определенных навыков научно-исследовательского характера.
3. Воспитание высокой культуры математического мышления.
4. Развитие у учащихся умения самостоятельно и творчески работать с учебной и научно-популярной литературой.
6. Расширение и углубление представлений учащихся о практическом значении математики
7. Воспитание учащихся чувства коллективизма и умения сочетать индивидуальную работу с коллективной.
8. Установление более тесных деловых контактов между учителем математики и учащимися и на этой основе более глубокое изучение познавательных интересов и запросов школьников.
9. Создание актива, способного оказать учителю математики помощь в организации эффективного обучения математике всего коллектива данного класса (помощь в изготовлении наглядных пособий, занятиях с отстающими, в пропаганде математических знаний среди других учащихся).
Слайд 4
Основными педагогическими принципами, обеспечивающими реализацию программы, являются:
учет
возрастных и индивидуальных особенностей каждого ребенка;
доброжелательный психологический климат
на занятиях; личностно-деятельный подход к организации учебно-воспитательного процесса;
подбор методов занятий соответственно целям и содержанию занятий и эффективности их применения;
оптимальное сочетание форм деятельности;
доступность.
Слайд 5
Математические хитрости
Математические фокусы
Математические ребусы и кроссворды
Математические игры
Интеллект-шоу
Поле
чудес
Математические чудеса и тайны
И многое другое…..
Слайд 6 Укладываем веревку с двумя петлями. На левом рисунке
палец можно поймать, если поместить его в петлю, отмеченную
стрелкой. На правом рисунке ни в одной петле палец поймать невозможно (щелкните на видео внизу чтобы увидеть).
Слайд 7 Учебный курс по математике «Задачи прикладной направленности» для учащихся 7
класса.
Тот, кто не знает математики, не может
узнать никакой
другой науки и даже не может обнаружить своего невежества.
Роджер Бэконния
Слайд 9
Задачи на расход материалов и денежных средств
Задачи
с числовыми великанами
Площадь участка
Задачи «Геометрия в природе»
Конкурс на составление задач
Оригаметрия
И многое другое……..
Слайд 10
103 – тысяча
106 – миллион
109 – биллион (миллиард)
1012
– триллион
1015 – квадриллион
1018 – квинтиллион
1021 – секстиллион
1024 –
септиллион1027 – октиллион
1030 – нониллион
1033 – дециллион
1036 – андециллион
1039 – дуодециллион
1042 – тредециллион
1045 – кваттордециллион
1048 – квиндециллион
1051 - сексдециллион
1054 – септендециллион
1057 – октодециллион
1060 – новемдециллион
1063 – вигинтиллион
10100 – гугол
Слайд 11
Игра-фокус.
- А сейчас я буду угадывать число, которое
ты загадал. Загадай число.
- любое?
- любое. Но не очень
большое, иначе вычисления будут громоздкими. Умножь задуманное число на 3, прибавь 5, прибавь задуманное число, умножь на 5, прибавь 5, умножь на 5. что получилось?- …
- Ты загадал…
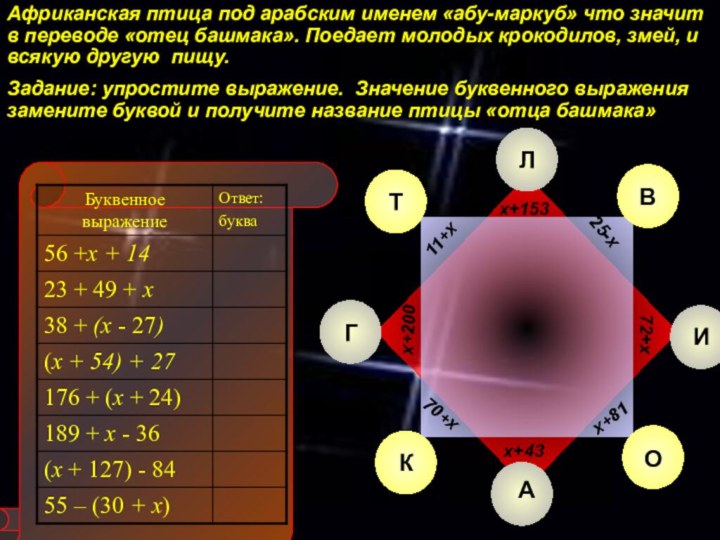
Слайд 12 Африканская птица под арабским именем «абу-маркуб» что значит
в переводе «отец башмака». Поедает молодых крокодилов, змей, и
всякую другую пищу.Задание: упростите выражение. Значение буквенного выражения замените буквой и получите название птицы «отца башмака»
Слайд 13
Японская мудрость издревле гласит:
«Великий квадрат не имеет пределов».
Попробуй
простую фигурку сложить,
И вмиг увлечет интересное дело.
А. Е.
Гайдаенко Слайд 14 Ори
Ками
бумага складывание
(что переводится «сложенная бумага») — древнее искусство складывания фигурок из бумаги.
Оригами
Слайд 17
Оригами в математике
Очень многое в оригами связано с
математикой. Разверните фигурку оригами и посмотрите на складки –
вы увидите лишь обилие многоугольников, соединенных друг с другом. В сложенном виде оригами представляет собой многогранник, фигуру с множеством плоских поверхностей.С точки зрения математики , целью оригамиста является точное определение местоположения одной или более точек листа, задающих складки, необходимые для формирования окончательного объекта.
Слайд 18
Да! Математику нам нужно знать!
Ведь без неё мы
кто! Природы дети!
А с ней творцы, создатели чудес!
Она в
познании, будто солнце светит,А без неё познание – тяжкий крест!
Так пусть мир чисел, формул, теорем,
Гипотез, лемм и аксиом прекрасных,
Нам другом будет, без исключения всем!
Чтоб всё в природе стало ясным и понятным!