- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Вычисления на старинных приборах (5 класс)
Содержание
- 2. Содержание. ВведениеГлава 1. История счетаГлава 2. Старинные приборы и их изучениеЗаключениеСписок литературы
- 3. Объектом исследования являются вычислительные приборы.Предметом исследования выступает процесс вычисления
- 4. ВВЕДЕНИЕ.За простыми действиями вычисления скрываются тайны истории
- 5. Экскурсия в магазин.Я побывала в сельском магазине
- 6. Моя мама, Сираева Гулия Маратовна, тоже работает в магазине. Она пользуется только электронными калькуляторами.
- 7. Кто может назвать самое древнее устройство, используемое для вычислений?
- 8. абакV – IV вв. до н.э.
- 9. В V веке до нашей эры в
- 10. У китайцев – «суан-пан»,у японцев – «серобян»,в России – «щоты».
- 11. «Потомком» абака можно назвать и русские счеты.
- 13. СложениеСогласно одному из возможных способов, сложение на
- 15. ВычитаниеВычитание на счётах выполняется «сверху вниз», то
- 16. УмножениеУмножение на однозначное число в общем случае
- 17. ДелениеДеление в общем виде заменяется вычитанием. Общий
- 19. Логарифмическая линейкаЛинейка Уатта - первая универсальная логарифмическая
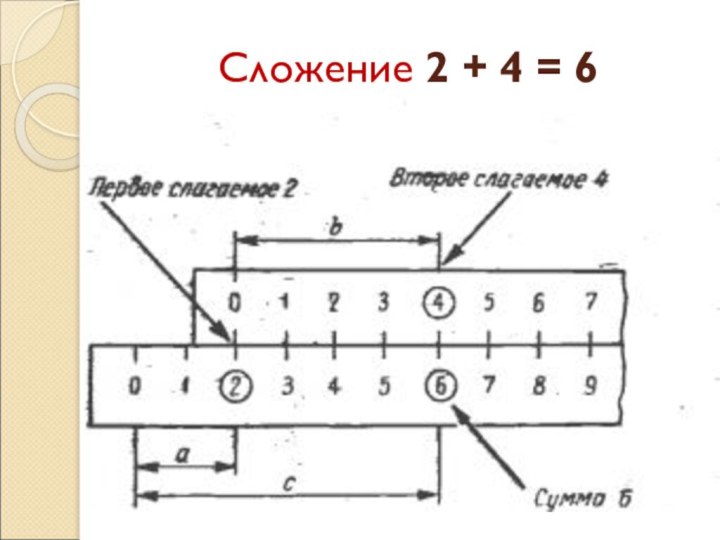
- 20. Сложение 2 + 4 = 6
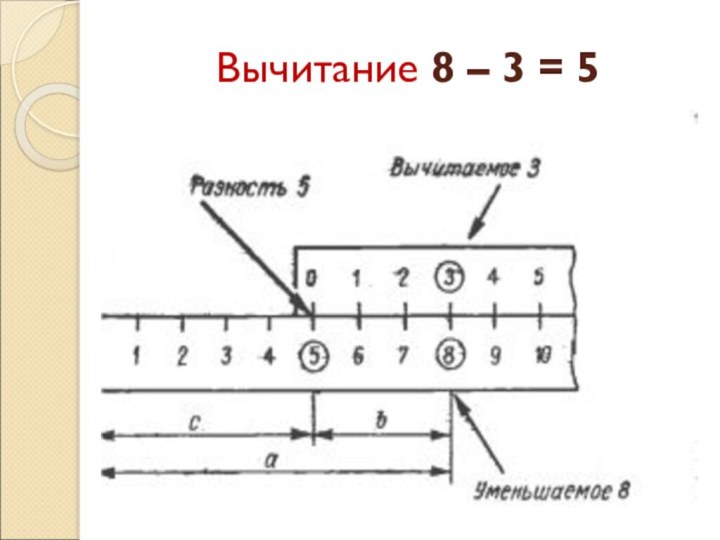
- 21. Вычитание 8 – 3 = 5
- 22. Умножение a ∙ b = с при a = 2, b = 3
- 23. Деление a:b = с при a = 8, b = 4На основной шкале корпуса
- 25. Арифмометр
- 26. АрифмометрВ XX веке широко использовался арифмометр –
- 27. Принцип работы арифмометра Феликс
- 28. СложениеЧтобы сложить два числа выполните следующие действия:Выставьте
- 29. ВычитаниеЧтобы вычесть одно число из другого выполните
- 30. УмножениеУмножение на небольшое числоВыставьте на рычажках первый
- 31. Умножение при помощи консолиУмножать на большие
- 32. Разберём пример: 1234 · 5678:Переместите консоль влево до
- 33. ДелениеРассмотрим случай деления 8765 на 432:Выставьте на
- 35. Первый калькулятор
- 36. Впервые над миниатюризацией арифмометров задумались два изобретателя:
- 38. Скачать презентацию
- 39. Похожие презентации
Содержание. ВведениеГлава 1. История счетаГлава 2. Старинные приборы и их изучениеЗаключениеСписок литературы


































Слайд 3
Объектом исследования являются вычислительные приборы.
Предметом исследования выступает процесс вычисления и
изучение приборов.
Цель: изучить приёмы вычислений старинными приборами и экспериментальным путем.
Задачи:
-
описать старинные приборы и опытно-экспериментальным путем выявить трудности в их использовании;-рассмотреть некоторые приборы и на конкретных примерах показать преимущества их использования.
Гипотеза: в старину говорили: « Вычисленье – мое мученье». Значит, раньше было сложно и трудно вычислять. Прост ли наш современный способ вычисления?
При работе я пользовалась следующими методами:
поисковый метод с использованием научной и учебной литературой, а также поиск необходимой информации в сети Интернет;
практический метод выполнения вычислений с применением старинных вычислительных приборов;
анализ полученных в ходе исследования данных.
Актуальность данной темы заключается в том, что использование старинных вычислительных приборов в формировании вычислительных навыков усиливает интерес учащихся к математике и содействует развитию математических способностей.
Слайд 4
ВВЕДЕНИЕ.
За простыми действиями вычисления скрываются тайны истории математики.
Случайно услышанные слова «Абак», «Счеты»,«Соробан»,«Арифмометр»,«Суаньпань» заинтриговали. Захотелось узнать эти
и другие приборы вычисления, сравнить их с нашими сегодняшними.Для того чтобы выяснить, знают ли современные школьники другие приборы вычисления, кроме калькуляторов и хотели бы узнать новые , был проведен устный опрос. Было опрошено 20 учащиеся. Этот опрос показал, что современные школьники не знают других приборов вычисления кроме калькулятора, так как редко обращаются к материалу, находящемуся за пределами школьной программы.
Слайд 5
Экскурсия в магазин.
Я побывала в сельском магазине и
спросила продавца Ханову Альфизю Ахматхановну, которая уже много лет
работает в магазине, как ей удобно работать на калькуляторе или на счетах. Она ответила: «Я перемножаю числа на калькуляторе, а складываю на счетах, мне удобнее работать на счетах так как я не сбиваюсь при счете на счетах да и покупатель видит на сколько он набрал товару, а кто не понимает как смотреть по счетам, то я и говорю мне не сложно. Сейчас молодежь которая работает в магазинах больше всего пользуются калькуляторами и вычислительными машинками, так как сейчас в наше время очень мало осталось старинных вычислительных приборов, но мне все же удобнее работать так».Слайд 6 Моя мама, Сираева Гулия Маратовна, тоже работает в
магазине.
Она пользуется только электронными калькуляторами.
Слайд 9
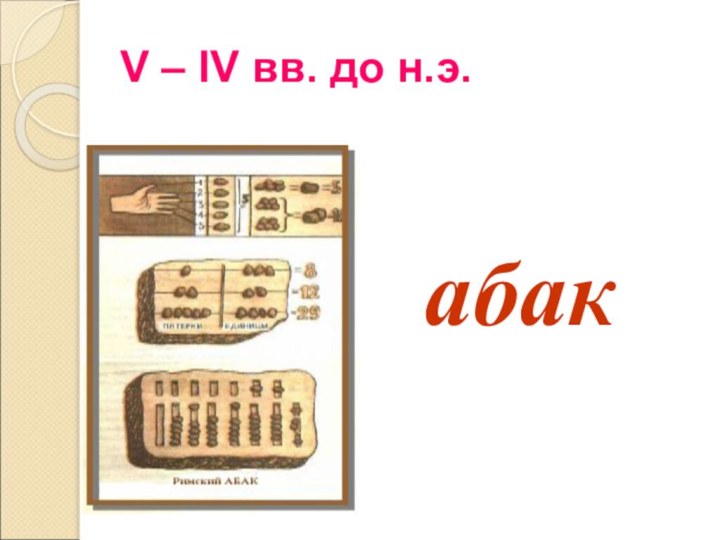
В V веке до нашей эры в Египте
и Греции получил распространение абак. Абак – это греческое
слово, которое переводится как счетная доска. Вычисления на абаке производились перемещением камешков по желобам на мраморной доске. Каждая полоска назначалась для откладывания тех или иных разрядов чисел.Так как у римлян камешек называли калькулюс, то счет на абаке получил название калькуляция. Отсюда и произошло слово калькулятор.
Подобные счетные инструменты распространились и развивались по всему миру. Например, китайский вариант абака назывался суан - пан.
Слайд 11
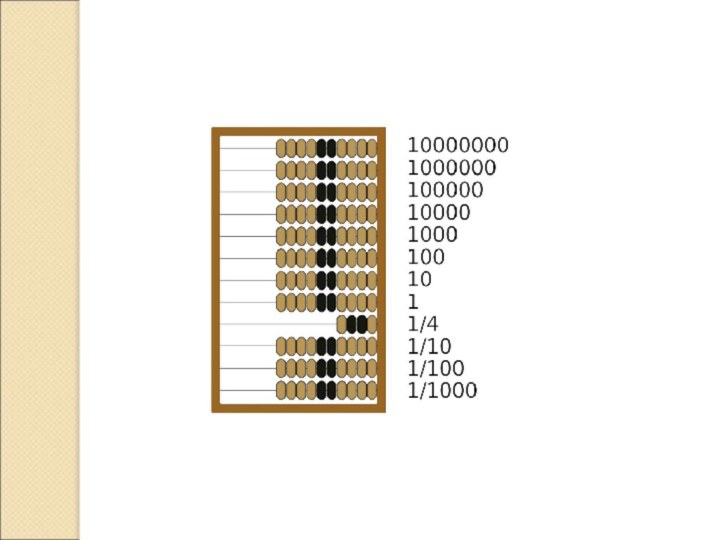
«Потомком» абака можно назвать и русские счеты. На
Руси счеты появились в шестнадцатом веке. Счеты были первым
механическим приспособлением в России. Этот "народный калькулятор" продержался на рабочих местах вплоть до середины девяностых годов. Счеты представляют собой деревянное основание, на котором укреплены металлические прутья, на которые нанизаны деревянные косточки. На каждом пруте находится десять косточек, за исключением разделителя рублей и копеек, на котором находится четыре косточки. Счеты предназначены для сложения и вычитания, причем при определенной сноровке скорость выполнения вычислений может превосходить скорость выполнения таких же вычислений, но с использованием калькулятора.
Слайд 13
Сложение
Согласно одному из возможных способов, сложение на счётах
выполняется «снизу вверх» (от младших разрядов к старшим). На
счётах «набирается» первое слагаемое, после чего поразрядно, от младшего разряда к старшему, производятся следующие действия:На проволоке, соответствующей разряду, перебрасывается влево столько косточек, сколько единиц в соответствующем разряде второго слагаемого.
Если на проволоке не хватает косточек для выполнения первого действия, то на проволоке слева оставляется столько косточек, сколько не хватило, а на следующей (находящейся выше) проволоке перебрасывается влево одна косточка.
После того, как будут выполнены действия со всеми разрядами, «набранное» на счётах число и будет результатом сложения.
Слайд 15
Вычитание
Вычитание на счётах выполняется «сверху вниз», то есть
от старших разрядов к младшим. В силу неприспособленности счётов
для работы с отрицательными числами всегда нужно из большего положительного числа вычитать меньшее положительное число. Если требуется вычесть из меньшего большее, числа следует поменять местами и оставить знак «в уме».На счётах «набирается» уменьшаемое, после чего поразрядно, от старшего разряда к младшему, производятся следующие действия:
На проволоке, соответствующей разряду, перебрасывается вправо столько косточек, сколько единиц в соответствующем разряде вычитаемого.
Если на проволоке не хватает косточек для выполнения первого действия, производится перенос разряда: слева оставляется (10 — n) косточек, где n — «недостающее» число косточек (чтобы не делать второе вычитание в уме, можно весь десяток косточек на данной проволоке перенести влево, после чего отбросить недостающее число косточек), а на находящейся выше проволоке отбрасывается вправо одна косточка
Если при переносе на проволоке, соответствующей старшему разряду, не хватает косточек, то выполняется перенос в следующий (ещё более старший) разряд и так до тех пор, пока на одной из проволок не окажется достаточного количества косточек. Так, например, при вычитании (1001 — 3) сначала на проволоке младшего разряда будет оставлено 8 косточек и потребуется перенос во второй разряд, затем — в третий, и только после этого на проволоке четвёртого разряда окажется достаточно косточек, чтобы завершить операцию.
Слайд 16
Умножение
Умножение на однозначное число в общем случае может
быть заменено на сложение множимого с самим собой соответствующее
количество раз. Целые многозначные числа перемножаются поразрядно, аналогично «умножению в столбик»:В качестве множимого выбирается то из двух чисел, которое содержит больше ненулевых цифр.
Множимое прибавляется к самому себе столько раз, сколько единиц в младшем (первом) разряде множителя.
Для каждого следующего разряда множителя множимое прибавляется к уже имеющемуся на счётах числу соответствующее количество раз, но со сдвигом на один разряд вверх. То есть для разряда десятков сложение производится со сдвигом на один разряд, сотен — на два и так далее.
Если в соответствующем разряде множителя стоит нуль, то, естественно, никакого сложения не производится, а просто делается сдвиг на одну проволоку вверх и переход к следующему разряду.
Когда будут произведены прибавления для всех ненулевых разрядов множителя, на счётах будет получен результат умножения. Положение десятичного разделителя при этом нужно учитывать в той позиции, где он был при первых сложениях (то есть сдвиги десятичного разделителя учитываются только в промежуточных операциях).
Если перемножаются нецелые числа, то операция выполняется точно так же (вычисления ведутся с целыми числами, десятичные разделители просто игнорируются). Десятичный разделитель ставится в нужную позицию вручную при записи результата.
Несмотря на громоздкость алгоритма, при выработанном навыке выигрыш времени по сравнению с расчётом на бумаге может быть значительным.
Слайд 17
Деление
Деление в общем виде заменяется вычитанием. Общий алгоритм
деления целых чисел выглядит следующим образом:
Делимое набирается на счётах
в нижней их части.Из старших разрядов делимого выбирается группа такого размера, чтобы составленное ею число было больше делителя, но меньше делителя, умноженного на десять. Десятичный разделитель мысленно переносится за младший разряд этой группы.
Из набранного числа (с учётом поставленного разделителя) делитель вычитается до тех пор, пока уменьшаемое не станет меньше делителя. При каждом успешном вычитании на верхней проволоке счёт переносится влево одна косточка.
По завершении вычитания десятичный разделитель мысленно передвигается на одну проволоку вниз. Далее вычитание делителя повторяется для нового уменьшаемого, а результат заносится на следующую (вторую, далее — третью и т. д.) проволоку.
Предыдущий пункт повторяется до тех пор, пока не закончится набранное на счётах число, либо пока не будет получено нужное число цифр результата.
На верхних проволоках по завершении всех операций будет набран результат деления. Положение десятичного разделителя при этом — такое же, как было у делимого.
Слайд 19
Логарифмическая линейка
Линейка Уатта - первая универсальная логарифмическая линейка,
пригодная для выполнения любых инженерных расчетов, была сконструирована в
1779 году выдающимся английским механиком Дж.Уаттом. Она получила название "сохо-линейки", по имени местечка близ Бирмингема, где работал Уатт.
Слайд 22
Умножение a ∙ b = с при a = 2, b = 3
На
основной шкале корпуса линейки (вторая снизу) выбирается первый сомножитель
и на него устанавливается начало основной, нижней, шкалы движка (она на лицевой стороне последнего и точно такая же, как основная шкала корпуса). На основной шкале движка волосок бегунка устанавливается на втором сомножителе. Ответ находится на основной шкале корпуса линейки под волоском. Если при этом волосок выходит за пределы шкалы, то на первый сомножитель устанавливают не начало, а конец движка (с числом 10).
Слайд 23
Деление a:b = с при a = 8, b = 4
На основной шкале корпуса линейки
выбирается делимое, на которое устанавливается волосок бегунка. Под волосок
подводится делитель, найденный на основной шкале движка. Результат определяется на основной шкале корпуса напротив начала или конца движка.
Слайд 25
Арифмометр
Появление первых механических счетных
машин и возрастающий спрос на них резко ускорили работы по совершенствованию технологии их изготовления. В 1822 г. конструктор Чарльз Ксавьер Томас (1785-1870) создал первый механический калькулятор и наладил серийное промышленное производство арифмометров. Арифмометры обладали относительно неплохой скоростью вычислений. Они перемножали два восьмиразрядных числа за 18 секунд.Вильгодт Теофил Однер (1845-1903) родился в Швеции. В 1866 году В. Т. Однер закончил Стокгольмский технологический институт. В 1869 году он приехал в Петербург, где и остался до конца своей жизни. В Петербурге он прежде всего обратился к своему соотечественнику Э. Л. Нобелю, который в 1862 г. основал на Выборгской стороне завод «Русский дизель». На этом заводе в 1874 г. был изготовлен первый образец арифмометра Однера.
Изобретение В.Однера - арифмометр с зубчаткой с переменным числом зубьев, - сыграло особую роль в развитии вычислительных машин. Его конструкция была настолько совершенна, что арифмометры этого типа модификации Феликс выпускались с 1873 г. практически без изменений в течение почти ста лет.
Слайд 26
Арифмометр
В XX веке широко использовался арифмометр – счетное
устройство, в основе которого лежали идеи Паскаля. Самым популярным
механическим вычислителем в советские времена являлся арифмометр системы Однера "Феликс".Для производства вычислений было необходимо крутить ручку - один раз для сложения или вычитания, и несколько раз для умножения и деления.
На арифмометре системы Однера можно было производить четыре арифметических действия - сложение, вычитание, умножение и деление. Модель оказалась настолько удачной, что ее разнообразнейшие модификации более чем полвека выпускались во многих странах мира. Во второй половине 19-го века арифмометры стали настолько популярны, что стали неотъемлемой частью оснащения рабочего места бухгалтера, инженера, банковского клерка, товароведа. Но они были довольно громоздки, дороги, а брать их с собой в поездку и вовсе было затруднительно.
Слайд 28
Сложение
Чтобы сложить два числа выполните следующие действия:
Выставьте на
рычажках первое слагаемое.
Поверните ручку от себя (по часовой стрелке).
При
этом число на рычажках вводится в счётчик суммирования.Выставьте на рычажках второе слагаемое.
Поверните ручку от себя. При этом число на рычажках прибавится к числу в счётчике суммирования.
Результат сложения — на счётчике суммирования.
Слайд 29
Вычитание
Чтобы вычесть одно число из другого выполните следующие
действия:
Выставьте на рычажках уменьшаемое.
Поверните ручку от себя.
При этом число
на рычажках вводится в счётчик суммирования.Выставьте на рычажках вычитаемое.
Поверните ручку на себя. При этом число на рычажках вычитается из числа на счётчике суммирования.
Результат вычитания — на счётчике суммирования.
Слайд 30
Умножение
Умножение на небольшое число
Выставьте на рычажках первый множитель.
Крутите
ручку от себя, пока на счётчике прокруток не появится
второй множитель.Результат умножения — на счётчике суммирования.
Слайд 31
Умножение
при помощи консоли
Умножать на большие числа можно
и вышеописанным способом, но тогда придётся поворачивать ручку очень
долго.Есть более рациональный способ — умножение при помощи консоли. Вспомним умножение столбиком: умножают на каждый разряд, записывая результаты со смещением. Смещение определяется тем, в каком разряде стоит второй множитель.
Для перемещения консоли используйте ручку спереди арифмометра (Феликс)
Слайд 32
Разберём пример: 1234 · 5678:
Переместите консоль влево до упора.
Выставьте
на рычажках первый множитель (1234).
Крутите ручку от себя, пока
на счётчике прокруток не появится первая цифра (справа) второго множителя (8).Переместите консоль на один шаг вправо.
Аналогично проделывайте пункты 3 и 4 для остальных цифр (2-ой, 3-ей и 4-ой). В итоге на счётчике прокруток должен быть второй множитель (5678).
Результат умножения — на счётчике суммирования.
Слайд 33
Деление
Рассмотрим случай деления 8765 на 432:
Выставьте на рычажках
делимое (8765).
Переместите консоль на пятый разряд (на четыре шага
вправо).Отметьте конец целой части делимого металлическими “запятыми” на всех счётчиках (запятые должны стоять в столбик перед цифрой 5).
Поверните ручку от себя. При этом делимое вводится в счётчик суммирования.
Сбросьте счётчик прокруток.
Выставьте на рычажках делитель (432).
Переместите консоль так, чтобы старший разряд делимого совместился со старшим разрядом делителя, т. е. на один шаг вправо.
Крутите ручку на себя, пока не получите отрицательное число (перебор).
Переместите консоль на один шаг влево.
Проделывайте пункты 8 и 9 до крайнего положения консоли.
Результат — модуль числа на счётчике прокруток, целая и дробная части разделены запятой. Остаток — на счётчике суммирования.
Слайд 35
Первый
калькулятор
Первый
калькулятор, выпущенный компанией — Casio 001, — был продан
в 1965 году. Первый в мире калькулятор Bell Punch/Sumlock's «ANITA» был выпущен в продажу в 1961 году по цене 2200 $. Однако, Casio заявляет, что их модель 001 была первым в мире калькулятором с функцией памяти.
Слайд 36
Впервые над миниатюризацией арифмометров задумались два изобретателя: учитель
музыки Куммер (Россия, 1846г) и немецкий бизнесмен Курт Херцштарк
(1938г). В результате появился первый механический калькулятор, названный счислителем Куммера. Калькулятор Куммера был плоским (5-7 мм), поскольку состоял лишь из подвижных зубчатых реек. Благодаря простоте, высокой надёжности и удобству в работе он приобрел огромную популярность и выпускался в разных странах и более 100 лет на заводах России. Другая модель - Курта Херцштарка – появилась зимой 1938 года, однако массовое производство не началось - помешала Вторая мировая война. Он получил название «Курта».В 1961 году на выставке промышленных достижений в Англии демонстрировался первый в мире полностью электронный калькулятор Anita MK 8 .
С него началась эра всеобщей калькуляторизации. Калькуляторы вставлялись в столы, портмоне, наручные часы, а с недавних пор всех их вытеснил калькулятор Windows.