Слайд 2
Комбинаторика - раздел математики, в котором изучаются вопросы
о том, сколько различных комбинаций, подчиненных тем или иным
условиям, можно составить из заданных объектов.
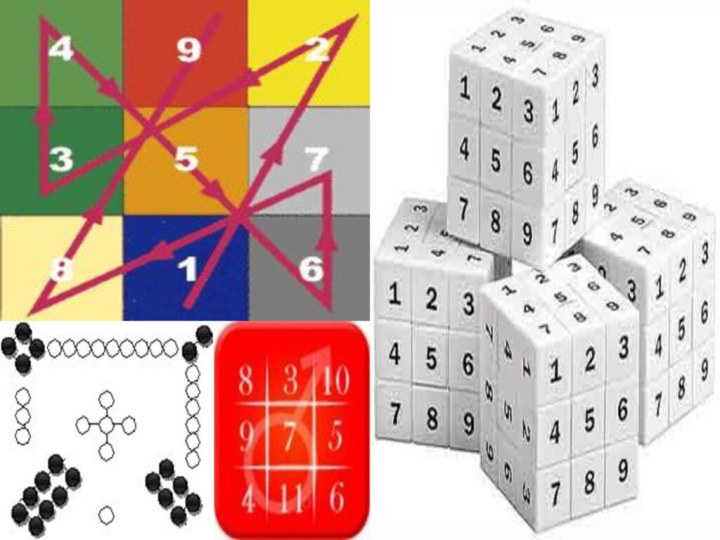
С аналогичными задачами, получившими название комбинаторных, люди столкнулись в глубокой древности. Уже несколько тысячелетий назад в Древнем Китае увлекались составлением магических квадратов, в которых заданные числа располагали так, что их сумма по всем горизонталям, вертикалям и главным диагоналям была одной и той же. В Древней Греции подсчитывали число различных комбинаций длинных и коротких слогов в стихотворных размерах, занимались теорией фигурных чисел, изучали фигуры, которые можно составить из частей разрезанного квадрата особым образом, и т.д.
Слайд 4
Комбинаторные задачи возникали и в связи с
такими играми, как шашки, шахматы, домино, карты, кости.
Слайд 5
Например: При игре в кости бросаются две
кости, и выпавшие очки складываются. Сколько существует комбинаций, в
которых сумма очков на верхних гранях равна двенадцати?
Решение: Каждый возможный исход соответствует функции F:{1,2}—>{1,2,3,4,5,6} - аргумент функции - это номер кости, значение— очки на верхней грани. Очевидно, что лишь 6+6 даёт нам нужный результат 12. Таким образом, существует лишь одна функция, ставящая в соответствие 1 число 6, и 2 число 6. Или, другими словами, существует всего одна комбинация, при которой сумма очков на верхних гранях равна двенадцати.
Слайд 6
Комбинаторика становится наукой лишь в XVII в.
– в период, когда возникла теория вероятностей.
Теория
вероятностей — раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.
Чтобы решать теоретико-вероятностные задачи, нужно было уметь подсчитывать число различных комбинаций, подчиненных тем или иным условиям. После первых работ, выполненных в XVI в. итальянскими учеными Дж. Кардано, Н. Тартальей и Г. Галилеем, такие задачи изучали французские математики Б. Паскаль и П. Ферма. Первым рассматривал комбинаторику как самостоятельную ветвь науки немецкий философ и математик Г. Лейбниц, опубликовавший в 1666 г. работу «Об искусстве комбинаторики», в которой впервые появляется сам термин «комбинаторный».
Слайд 7
Чтобы решать теоретико-вероятностные задачи, нужно
было уметь подсчитывать число различных комбинаций, подчиненных тем или
иным условиям. После первых работ, выполненных в XVI в. итальянскими учеными Дж. Кардано, Н. Тартальей и Г. Галилеем, такие задачи изучали французские математики Б. Паскаль и П. Ферма. Первым рассматривал комбинаторику как самостоятельную ветвь науки немецкий философ и математик Г. Лейбниц, опубликовавший в 1666 г. работу «Об искусстве комбинаторики», в которой впервые появляется сам термин «комбинаторный».
Слайд 8
Комбинаторные задачи физики, химии, биологии, экономики и других
наук, которые не поддавались ранее решению из-за трудоемкости вычислений,
стали успешно решаться на ЭВМ. В результате этого комбинаторные методы исследования все глубже проникают во многие разделы науки и техники. Простейшими примерами комбинаторных конфигураций или, другими словами, конструкций являются перестановки, размещения и сочетания. Комбинаторные вычисления требуют комбинаторного анализа для установления свойств и оценки применимости алгоритмов.
Слайд 9
Например: Агентство недвижимости, база данных. Запись –
пара (предложение, спрос). Найти варианты обмена, т.е. такие пары,
где первая компонента одной совпадает со второй компонентой другой.
Решение: Простейший вариант поиска – “лобовой”, трудоемкость n´ (n–1)/2. Если на одну проверку нужна 1 миллисекунда, то при n = 100 потребуется около 5 секунд, при n=100 000 – 5´ 106 сек, т.е. около 1389 часов. Непригодный алгоритм!
Слайд 10
Чаще всего в комбинаторных вычислениях используются следующие
конструкци:
Сочетание — это комбинации, составленные из данных п элементов
по т элементов, которые различаются хотя бы одним элементом. Сочетания бывают без повторений - n различные элементы, взятых по m, а бывают с повторениями - n элементы, взяты по m и эти элементы в наборе могут повторяться. Стоит заметить, что в сочетаниях не учитывается порядок элементов.
Слайд 11
Примере: Пусть имеется три элемента: a, b и
c. Из этих трёх элементов, в отличие от размещений,
можно составить такие сочетания по два элемента: ab, ac, bc. Все приведённые сочетания отличаются друг от друга хотя бы одним элементом.
Существует такое выражение, как, число сочетаний, т.е., сколькими способами можно выбрать из них т предметов (безразлично, в каком порядке)? Число способов такого выбора равно:
Знак n! читается: «n факториал» - обозначает произведение всех целых чисел от 1 до n. Оказывается удобным рассматривать также 0!, полагая его равным 1.
Слайд 12
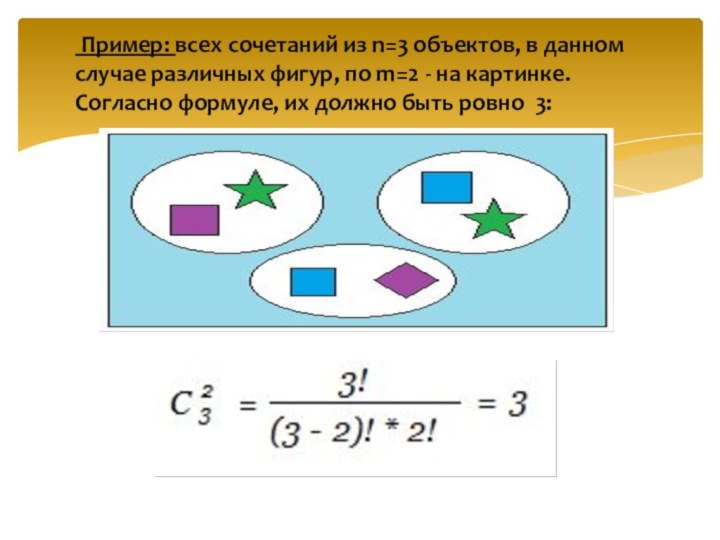
Пример: всех сочетаний из n=3 объектов, в
данном случае различных фигур, по m=2 - на картинке.
Согласно формуле, их должно быть ровно 3:
Слайд 13
Воспользуемся азбукой Морзе, состоящей всего из двух символов:
точка ● и тире ─ и построим слова разной
длины. Каждая буква алфавита может быть использована один раз, несколько раз или ни разу.
Слово длины 1:
Слово длины 2:
Слово Длины 3:
Слайд 14
Например: Подсчитать количество слов длины п в алфавите
из k букв.
Решение: В
слове длины п имеется п мест. На первое место ставим любую из k букв. При заполнении очередного места число возможностей увеличивается в k раз.
k * k * k * ...* k = kⁿ. п раз
И так, мы пришли к выводу, что число слов длины п в алфавите из k букв равно kⁿ.
Слайд 15
Размещение. Ряд, заполненный объектами данного множества, т.е., расположение
объектов на определённых местах называется размещением.
В отличие от
пункта 1, где букву можно использовать не один раз, в данном случае, поместив какой-либо объект на определённое место он не может быть использован вторично, т.е., мы забираем его из множества и больше его у нас нет.
Например: Подсчитать число А размещений п объектов на k местах. Решение: На первое место ставим любой из п объектов. На каждом следующем шаге число возможностей уменьшается на единицу: п(п — 1)(п — 2)... = п(п — 1)...(п — k + 1). k множителей.
Стоит обратить внимание, что последний множитель равен п(п — 1)...(п — k + 1).
Заметим, если k > п, то один из множителей будет равен нулю, поскольку нельзя п объектами занять число мест большее, чем п. Ответ данного решения можно записать в виде таблицы:
Слайд 16
Рассмотрим пример: Из элементов множества {a, b, c,
d} составим все возможные пары, но что бы элементы
в них не повторялись. В первой строке запишем все пары с первым элементом а, во второй — все пары с первым элементом b и т. д. Получи следующий результат:
(a, b), (a, c), (a,d)
(b, a), (b, c), (b, d)
(c, a), (c, b), (c, d)
(d, a), (d, b), (d, c)
Каждую пару из этой таблицы, составленную из множества {a, b, c, d} в комбинаторике называют размещением из 4 элементов по 2. Число всех таких размещений обозначают так: А² и читают — «А из четырёх по два».
Теперь можно сделать соответствующую запись:
А² = 4 * 3 = 12
Размещения — это могут быть пары, тройки, четвёрки т. д.
Слайд 17
Размещения — это могут быть пары, тройки, четвёрки
т.д.
Приведём ещё один пример: Из 12 учащихся нужно
отобрать по одному человеку для участия в городских олимпиадах по математике, физике, истории и географии. Каждый из учащихся должен участвовать только в одной олимпиаде. Сколькими способами можно это сделать? Решение: Каждая группа учащихся, направляемая на олимпиаду в составе 4 человек, отличается либо учащимися, либо порядком, который определяет, по какому предмету будет соревноваться учениек. Поэтому число способов отбора учащихся равно числу размещений из 12 по 4:
А⁴ = 12 * 11 * 10 * 9 = 11 880
Общая формула для вычисления числа размещений будет выглядеть следующим образом:
Слайд 18
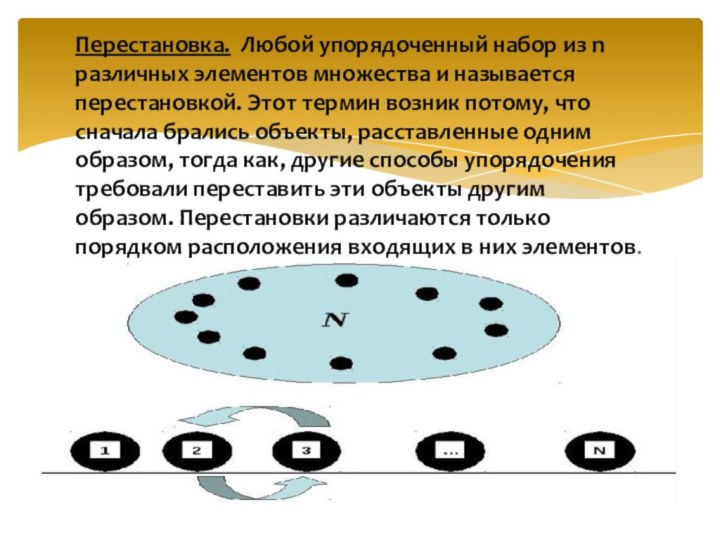
Перестановка. Любой упорядоченный набор из n различных элементов
множества и называется перестановкой. Этот термин возник потому, что
сначала брались объекты, расставленные одним образом, тогда как, другие способы упорядочения требовали переставить эти объекты другим образом. Перестановки различаются только порядком расположения входящих в них элементов.
Слайд 19
Например: Сколькими способами можно установить порядок следования друг
за другом n различных предметов?
Решение: Число способов равно:
Pn = 1* 2 * 3... * n = n!
Пример всех перестановок из n=3 объектов, различных фигур - на картинке.
Согласно формуле, их должно быть ровно 6.
С ростом числа объектов количество перестановок очень быстро растёт и изображать их наглядно становится затруднительно. Например, число перестановок из 10 предметов - уже 3628800 (больше 3 миллионов!).
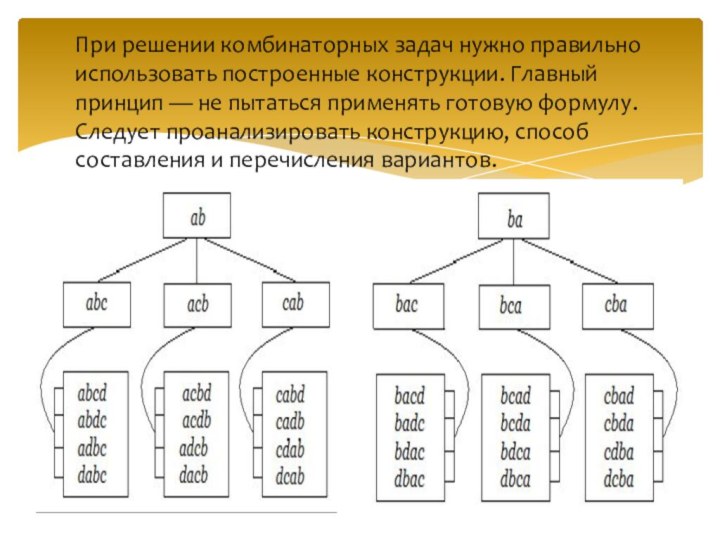
Заметим, что очень удобно процесс перестановок осуществлять путём построения специальной схемы, которая называется дерево возможных вариантов. Дерево помогает увидеть путь решения, учесть все варианты и избежать повторений. Рассмотрим построение дерева возможных вариантов:
Слайд 20
При решении комбинаторных задач нужно правильно использовать построенные
конструкции. Главный принцип — не пытаться применять готовую формулу.
Следует проанализировать конструкцию, способ составления и перечисления вариантов.
Слайд 21
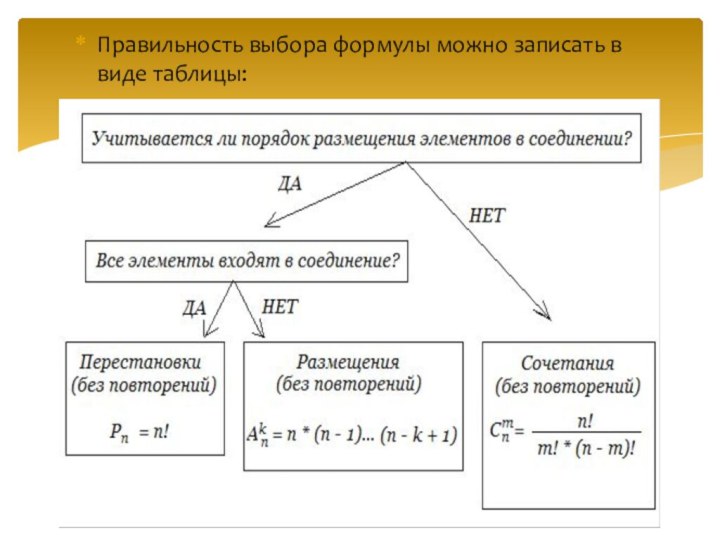
Правильность выбора формулы можно записать в виде таблицы:
Слайд 22
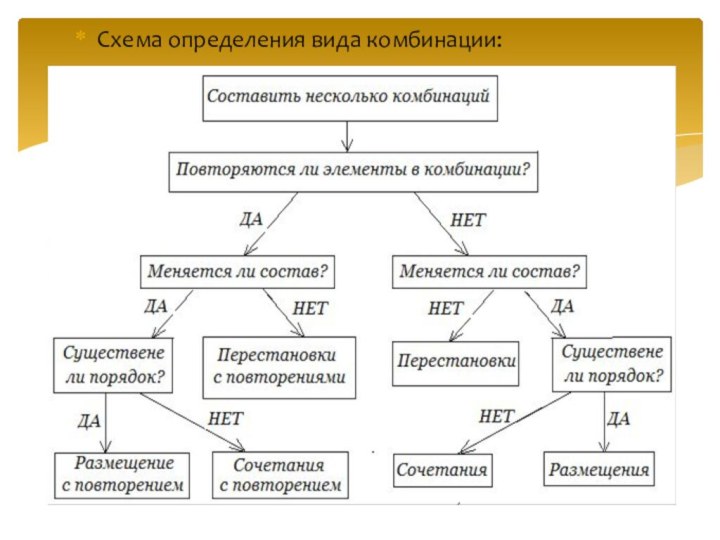
Схема определения вида комбинации:
Слайд 23
Пусть в множестве А имеется m элементов,
а в множестве В – n элементов. Если у
множеств А и В нет общих элементов, то в их объединении число элементов равно т + п
Можно сказать так, что если в двух мешках лежат разные предметы, и мы ссыпаем их вместе, то, чтобы найти их общее количество, надо сложить количества предметов в каждом из мешков.
Если для конечного множества Х мы через |Х| обозначим количество его элементов, то правило сложения можно записать так:
Правило суммы (сложения).
Слайд 24
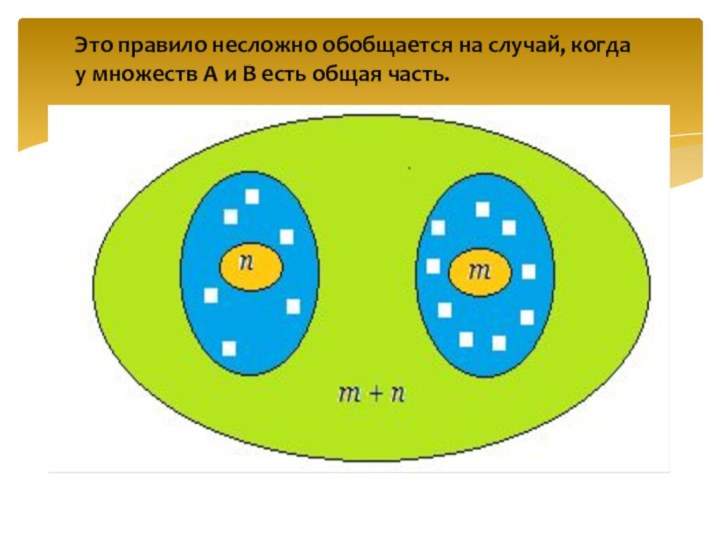
Это правило несложно обобщается на случай, когда у
множеств А и В есть общая часть.
Слайд 25
Число пар, составленных из элементов множеств А и
В, равно произведению количеств элементов этих множеств.
Множество пар элементов
двух множеств часто обозначают с помощью знака произведения. Тогда правило умножения можно записать так:
Например: Если на первой полке стоит 5 книг, а на второй 10, то выбрать одну книгу с первой полки и одну со второй можно 5*10=50 способами.
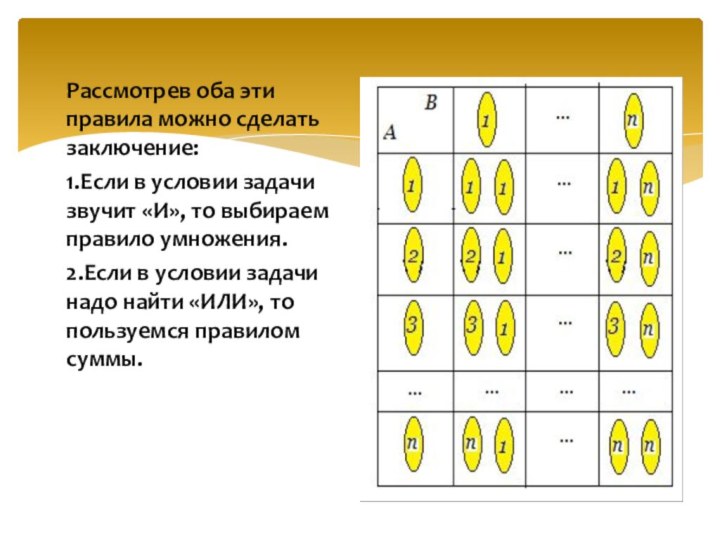
Правило умножения легко пояснить с помощью таблицы. Если составить таблицу и занумеровать её строчки элементами множества А, а столбцы — элементами множества В, то клетки таблицы будут соответствовать парам (a, b), где а є A, b є В. Число клеток таблицы, очевидно, равно произведению числа строк и числа столбцов.
Правило умножения.
Слайд 26
Рассмотрев оба эти правила можно сделать заключение:
1.Если в
условии задачи звучит «И», то выбираем правило умножения.
2.Если в
условии задачи надо найти «ИЛИ», то пользуемся правилом суммы.
Слайд 27
Мы разобрали простейшие случаи, когда множества не пересекаются.
А как быть со множествами, которые пересекаются? Для них
существует правило включений и исключений. Данное правило распространяется на произвольное число множеств. Все различные комбинации элементов «A или B» можно выбрать по формуле:
Правило включений и исключений.
Слайд 28
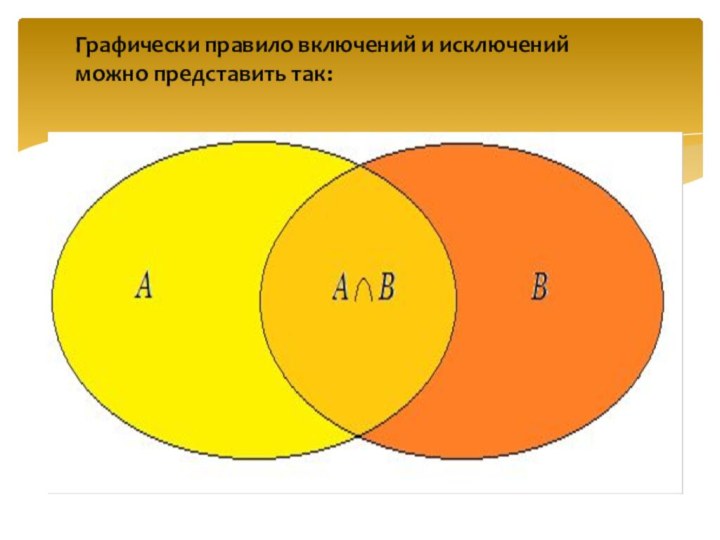
Графически правило включений и исключений можно представить так:
Слайд 29
Первый пример: Число слагаемых. Выяснить, сколько одночленов получится
при умножении «скобки на скобку» данного произведения :
(a +
b + c) * (a² + b² + c² – ab – ac bc)?
Этот же вопрос можно задать другими словами: Сколько пар можно составить из одночленов в первой и второй скобках?
Решение заключается в следующем - выберем любой из трёх одночленов в первой скобке и любой из шести одночленов во второй скобке — число пар равно 3 * 6 = 18. В данном случае использовали правило умножения.
Слайд 30
Второй пример: Число слов. В алфавите 4 буквы.
Сколько можно составить слов из трёх букв этого алфавита?
Применяем правило сложения, т.к. Число слов длины п из алфавита в 4 буквы равно 4ⁿ.
4 + 4² + 4³ = 4 + 16 + 64 =84.
Третий пример: Число учеников. В классе каждый ученик изучает какой-нибудь язык, при этом 20 учеников изучают английский, 12 — французский, а 7 учеников — оба языка. Надо выяснить сколько учеников в классе?
Если сложить количество учеников, изучающих английский и французский языки, то мы учтём всех учеников, но тех, которые изучают два языка, посчитаем дважды. Для решения этой задачи применяем правило включения — исключения. Решение будет таковым:
20 + 12 — 7 = 25.