- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по теме: Математика в начальной школе в инклюзивном классе. Обучение умственно отсталого ученика.
Содержание
- 2. Математика, являясь одним из самых трудных предметов
- 3. В процессе обучения математике учащиеся с УО
- 4. двигательная недостаточность, скованность движений или, наоборот, импульсивность,
- 5. несовершенство анализа приводит к тому, что умственно
- 6. Специальные требования к обучению: Замедленность темпа обучения,
- 7. предоставление стола с математическими предметами для справочной
- 8. постепенное усложнение материала, с увеличением количества тренировочных
- 9. рекомендуется включать элементы геометрии в каждый урок
- 10. Для успешного обучения учащихся с нарушением интеллекта
- 11. Задачи обучения математике обучающихся с умственной отсталостьюФормирование
- 12. Образовательные задачи: формировать (формирование) у учащихся представления
- 13. Коррекционно-развивающие задачи: корригировать внимание (произвольное, непроизвольное, устойчивое,
- 14. Коррекционно-развивающие задачи: коррекция и развитие памяти (кратковременной,
- 15. Воспитательные задачи: воспитывать интерес к учебе,
- 16. Коррекционный урок Коррекционные уроки применяются для практической
- 17. Учителю на заметкуОт предметно- манипуляторногомышления к наглядно- образному мышлению через личный опыт учащегося.
- 18. «Рамка»Учащихся, испытывающих трудности можно научить работать с
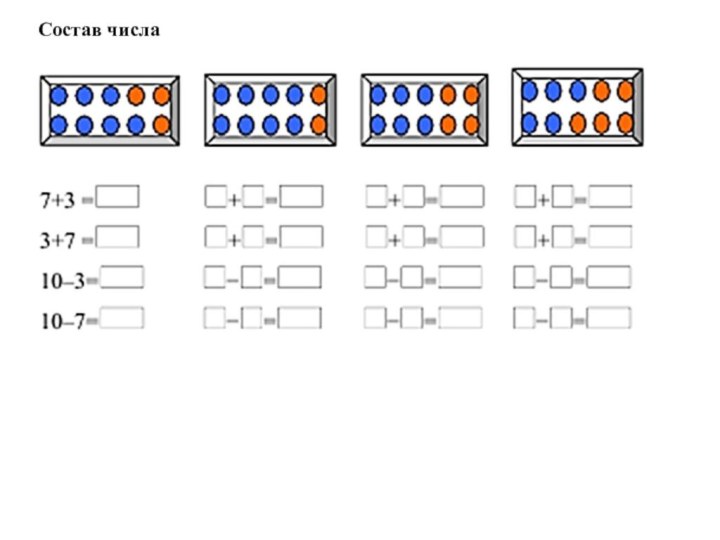
- 19. Состав числа
- 20. Далее учитель объясняет, что единицы можно представить
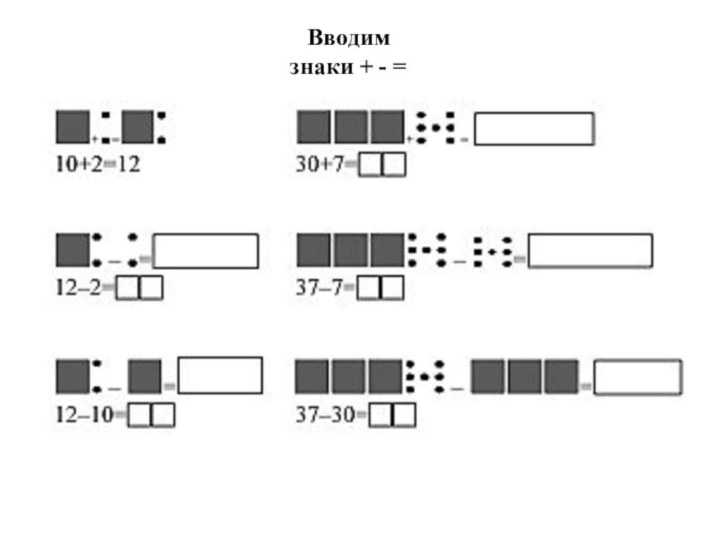
- 21. Вводим знаки + - =
- 22. Графическая запись этих примеров выполняется учениками с
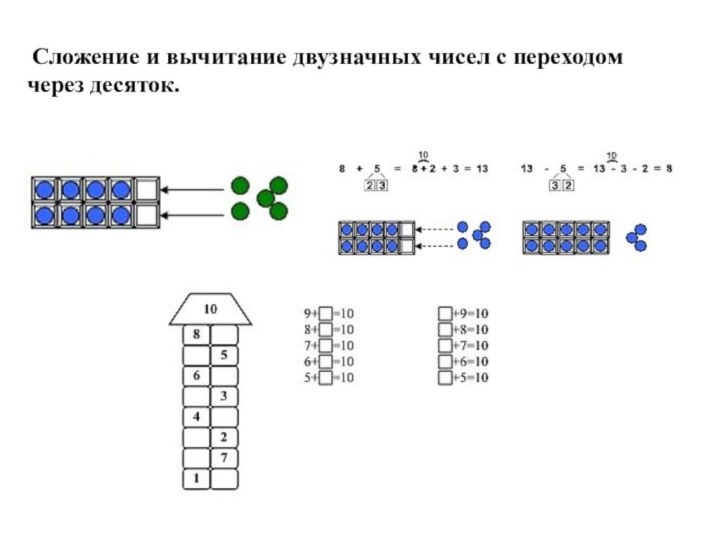
- 23. Сложение и вычитание двузначных чисел с переходом через десяток.
- 24. Случаи сложения и вычитания, основанные на знании состава однозначных чисел и круглых десятков.
- 25. Состав однозначных чисел и состав
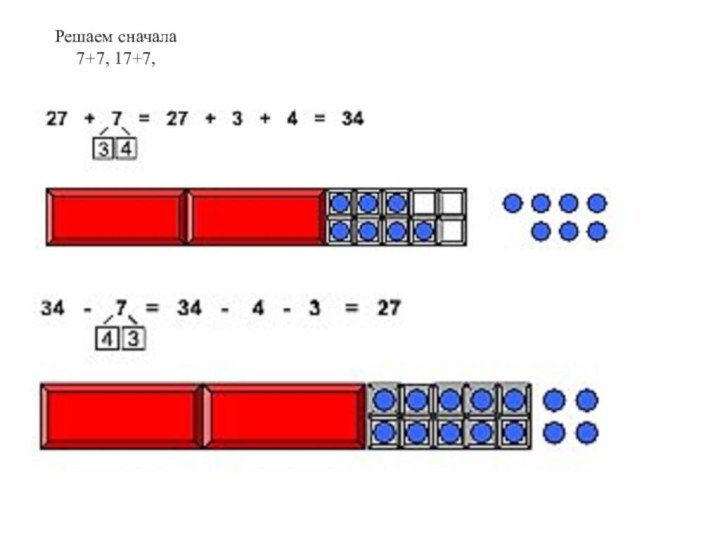
- 26. Решаем сначала 7+7, 17+7,
- 27. Для учащихся со средним и высоким уровнями
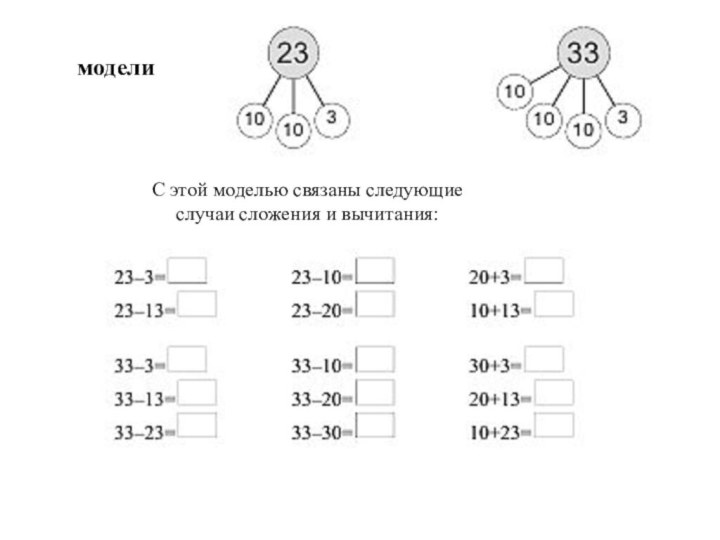
- 28. моделиС этой моделью связаны следующие случаи сложения и вычитания:
- 29. Эта модель позволяет рассмотреть больше случаев сложения
- 30. Используя эту модель, можно разработать
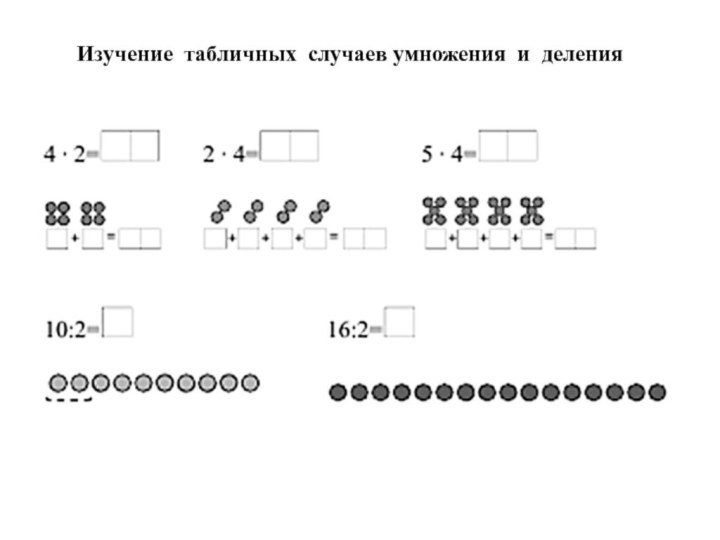
- 31. Изучение табличных случаев умножения и деления
- 32. Учащиеся с трудностями в обучении достаточно долго
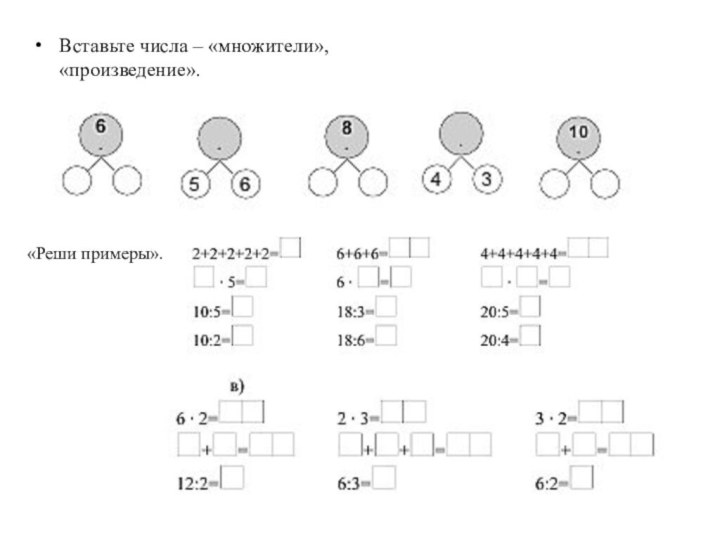
- 33. Вставьте числа – «множители», «произведение». «Реши примеры».
- 34. Многозначные числаДля учащихся со средним или
- 35. Для облегчения решения примеров на сложение и
- 36. Подготовительный этап знакомства с уравнением
- 37. Работа над задачами Умением решать арифметические задачи,
- 38. 4.Учителю необходимо самому или с помощью сильных
- 39. Последовательность работы над усвоением содержания задачи с
- 40. 2. Поиск решения задачи. 3. Решение задачи.
- 41. 7. Последующая работа над решенной задачей: а)
- 42. Иллюстрация задачи способствует обогащению у учащихся имеющихся
- 43. Работа над трудными словами организуется ранее, например,
- 44. Используются основные виды иллюстраций: 1. Предметная иллюстрация
- 45. Задачи на деление по содержанию также удобно
- 46. Задача: Масса двух одинаковых чемоданов равна
- 47. Среди схематических иллюстраций в рабочей тетради широко
- 48. Графическая форма записи – это запись содержания
- 49. Так же достаточно широко используется в рабочей
- 50. Большинство учащихся с низким уровнем нуждаются
- 51. Скачать презентацию
- 52. Похожие презентации
Математика, являясь одним из самых трудных предметов для восприятия ребёнка с умственной отсталостью (интеллектуальными нарушениями), готовит его к жизни и овладению доступными профессионально-трудовыми навыками.

































Слайд 3 В процессе обучения математике учащиеся с УО сталкиваются
со следующими проблемами:
узость, не целенаправленность и слабая активность восприятия
создают определенные трудности в понимании задачи, математического задания. Учащиеся воспринимают задачу не полностью, а фрагментарно, т.е. по частям, а несовершенство анализа и синтеза не позволяет эти части связать в единое целое, установить между ними связи и зависимости и, исходя из этого, выбрать правильный путь решения;фрагментарность восприятия является одной из причин ошибочного вычисления значения числовых выражений, содержащих два действия;
несовершенство зрительного восприятия (зрительного анализа и синтеза) и моторики учащихся. Это проявляется в обучении письму вообще и цифр в частности. Несовершенство зрительных восприятий, трудности пространственной ориентировки приводят к тому, что учащиеся не видят клетки и строки и не понимают их значения.
Слайд 4 двигательная недостаточность, скованность движений или, наоборот, импульсивность, расторможенность
создают значительные трудности в пересчете предметов: ученик называет один
предмет, а берет или отодвигает сразу несколько предметов, т.е. называние чисел опережает показ или, наоборот, показ опережает называние чисел.трудность в выработке новых условных связей, возникнув, они оказываются непрочными, хрупкими, а главное, недифференцированными. Слабость дифференциации нередко приводит к уподоблению знаний. Учащиеся быстро утрачивают те существенные признаки, которые отличают одну фигуру от другой, один вид задачи от другого, те признаки, которые позволяют различать числа, действия, правила.
отмечается «застревание» на принятом способе решения примеров, задач, практических действий. С трудом происходит переключение с одной умственной операции на другую, качественно иную.
Слайд 5 несовершенство анализа приводит к тому, что умственно отсталые
школьники сравнение задач, геометрических фигур, примеров, математических выражений проводят
поверхностно, не проникая во внутренние связи и отношения.низкий уровень мыслительной деятельности школьников с нарушением интеллекта затрудняет переход от практических действий к умственным.
бедность словаря, непонимание значения слов, отсутствие связной устной речи.
трудность в развитии зрительного восприятия и узнавания;
трудности в развитии пространственных представлении и ориентировки;
ограниченность в развитии слухового внимания и памяти;
недостаточность процесса запоминания и воспроизведения учебного материала;
трудности в развитии наглядно-образного и наглядно-действенного мышления;
трудности в развитии переключаемости внимания.
Слайд 6
Специальные требования к обучению:
Замедленность темпа обучения, что соответствует
замедленности протекания психических процессов;
упрощение структуры ЗУН в соответствии с
психофизическими возможностями ученика;осуществление повторности при обучении на всех этапах и звеньях урока;
максимальная опора на чувственный опыт ребенка, что обусловлено конкретностью мышления ребенка;
максимальная опора на практическую деятельность и опыт ученика;
опора на более развитые способности ребенка;
осуществление дифференцированного руководства учебной деятельностью ребенка, предусматривающего проектирование, направление и регулирование, а вместе с тем и исправление действий учащихся членением целостной деятельности на отдельные части, операции и др.
разрешение использовать калькулятор.
размещение малого количества заданий на одном листе с упражнениями (например, от 4 до 6 заданий на странице).
использование малого количества заданий для получения оценки;
Слайд 7
предоставление стола с математическими предметами для справочной информации;
обеспечение
каждого ученика визуальным числовым рядом;
поэтапное представление проблемных заданий;
использование
визуальных пособий (картинок, графиков, таблиц, перфокарт и др.); необходимо многократное повторение основного материала.
изучение материала небольшими дозами, учитывая психологические особенности и возможности этих детей;
Слайд 8 постепенное усложнение материала, с увеличением количества тренировочных упражнений;
обязательное решение арифметических задач на уроке, поскольку данный вид
работы, развивая способности рассуждать, анализировать, производить умозаключения, помогает коррекции недостатков мыслительной деятельности и речи детей с трудностями в обучении; необходимо увеличение внимания к устному счету. Учащиеся, выполняя счетные операции в уме, совершенствуют и развивают такие психические процессы как память и внимание. Упражняться в устном счете необходимо на каждом уроке математики, т.к. без тренировок вычислительные навыки ослабевают. Для учащихся с трудностями в обучении устный счет дается с большим трудом, и, как следствие, нелюбим большинством учащихся, необходимо представлять его в игровой форме. Игровая форма позволяет повысить мотивацию, интерес к заданиям такого рода;
Слайд 9 рекомендуется включать элементы геометрии в каждый урок математики
(приблизительно на 10 мин), в зависимости от цели и
вида конкретного урока;создание, поддержание доброжелательной атмосферы на уроке. Необходимо поощрение учащихся даже за самые незначительные успехи, за сообразительность, а чаще просто за упорство, это создает ощущение внутреннего комфорта и дополнительно повышает мотивацию учения, положительное отношение к уроку математики и т.п.;
необходима алгоритмизация деятельности, которая может быть представлена в инструкциях, памятках, схемах-опорах, таблицах-опорах и пр.). С помощью этих опор учащимся легко будет проконтролировать ход выполнения задания, результат, найти этап, на котором была совершена ошибка, и исправить ее.
планировать меньший по объему материал для учащихся с особыми образовательными потребностями, чем для остальных учащихся;
небольшой объем домашнего задания, а также наличие подробной инструкции к нему.
проведение внеклассных мероприятий, повышающих интерес к математике;
обязательное проведение на уроках математики физминуток, что снимет умственное перенапряжение и поможет переключить учащихся на другой вид деятельности;
Слайд 10 Для успешного обучения учащихся с нарушением интеллекта математике
учитель должен хорошо изучить состав учащихся, знать причины умственной
отсталости ученика, обучающегося инклюзивно. Знать и понимать особенности его поведения, определять его потенциальные возможности, чтобы наметить пути включения его во фронтальную работу класса с учетом его психофизических особенностей, степени дефекта. Это даст возможность правильно осуществить дифференцированный и индивидуальный подход к учащимся с ОВЗ, наметить пути коррекционной работы, т.е. обеспечить их всестороннее развитие.
Слайд 11
Задачи обучения математике обучающихся с умственной отсталостью
Формирование доступных
математических знаний и умений, необходимых для развития учебно-познавательных, учебно-практических,
житейских и профессиональных задач и развитие способности их использования при решении в соответствии с возрастом задач;Коррекция и развитие познавательной деятельности и личностных качеств обучающихся с умственной отсталостью средствами математики с учётом их индивидуальных возможностей.
Формирование положительных качеств личности: аккуратности, настойчивости, трудолюбия, самостоятельности, терпеливости, любознательности, умений планировать свою деятельность, доводить начатое дело до конца, осуществлять контроль и самоконтроль.
Слайд 12
Образовательные задачи:
формировать (формирование) у учащихся представления о …;
выявить (выявлять)…; знакомить, познакомить, продолжать знакомить…; уточнить…; расширить…; обобщить…;
систематизировать…; дифференцировать…; учить применять на практике…; учить пользоваться…; тренировать…; проверить….
Слайд 13
Коррекционно-развивающие задачи:
корригировать внимание (произвольное, непроизвольное, устойчивое, переключение внимания,
увеличение объема внимания) ;
коррекция и развитие связной устной
речи (регулирующая функция, планирующая функция, анализирующая функция, орфоэпически правильное произношение, пополнение и обогащение пассивного и активного словарного запаса, диалогическая и монологическая речь) через выполнение…; коррекция и развитие связной письменной речи (при работе над деформированными текстами, сочинением, изложением, творческим диктантом)…;
Слайд 14
Коррекционно-развивающие задачи:
коррекция и развитие памяти (кратковременной, долговременной…);
коррекция
и развитие зрительных восприятий;
развитие слухового восприятия…;
коррекция и
развитие тактильного восприятия…; коррекция и развитие мелкой моторики кистей рук (формирование ручной умелости, развитие ритмичности, плавности движений, соразмерности движений)…;
коррекция и развитие мыслительной деятельности (операций анализа и синтеза, выявление главной мысли, установление логических и причинно-следственных связей, планирующая функция мышления)…;
коррекция и развитие личностных качеств учащихся, эмоционально-волевой сферы (навыков самоконтроля, усидчивости и выдержки, умение выражать свои чувства…;
Слайд 15
Воспитательные задачи:
воспитывать интерес к учебе, предмету; воспитывать
умение работать в парах, в команде; воспитывать самостоятельность; воспитывать
нравственные качества (любовь, бережное отношение к …, трудолюбие, умение сопереживать и т. п.)Формулировка задач на урок зависит от темы урока, подобранных заданий и типа урока. Например, на уроке изучения нового материала – дать понятия, познакомить; на уроке закрепления знаний – закрепить, повторить и т. п.
Слайд 16
Коррекционный урок
Коррекционные уроки применяются для практической реализации коррекции
познавательной сферы, речи, закрепления изученных понятий, графомоторных и моторных
функций, каллиграфических навыков письма т. д. На этих уроках осуществляется исправление, уточнение, перестройка действий, реализуемые в наблюдении объектов или явлений, узнавании, назывании, сравнении, классификации, описании, выделении главного, обобщении. При этом широко используются подвижные игры и физические упражнения на развитие всех анализаторов.
Слайд 17
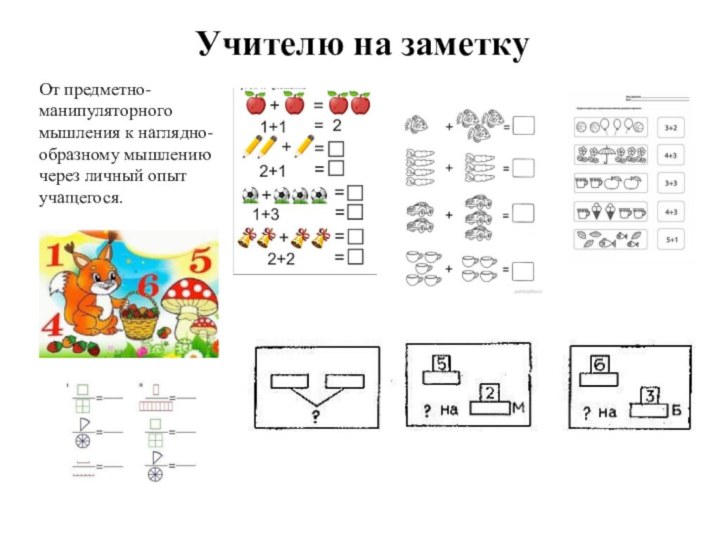
Учителю на заметку
От предметно- манипуляторного
мышления к наглядно- образному
мышлению через личный опыт учащегося.
Слайд 18
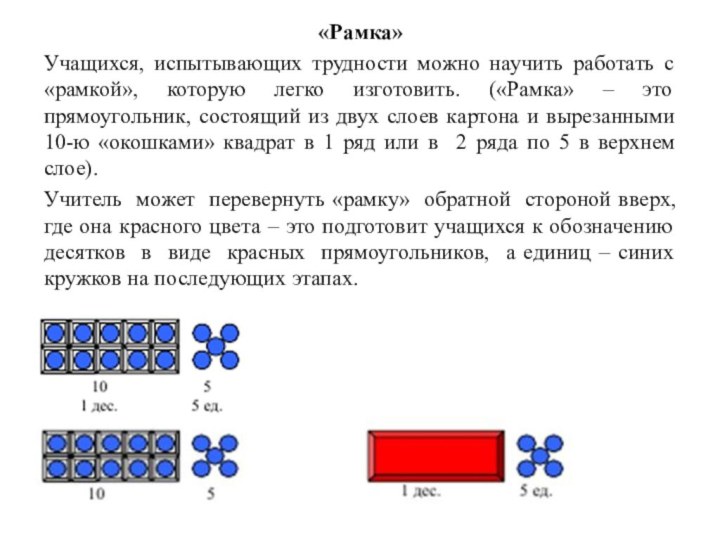
«Рамка»
Учащихся, испытывающих трудности можно научить работать с «рамкой»,
которую легко изготовить. («Рамка» – это прямоугольник, состоящий из
двух слоев картона и вырезанными 10-ю «окошками» квадрат в 1 ряд или в 2 ряда по 5 в верхнем слое).Учитель может перевернуть «рамку» обратной стороной вверх, где она красного цвета – это подготовит учащихся к обозначению десятков в виде красных прямоугольников, а единиц – синих кружков на последующих этапах.
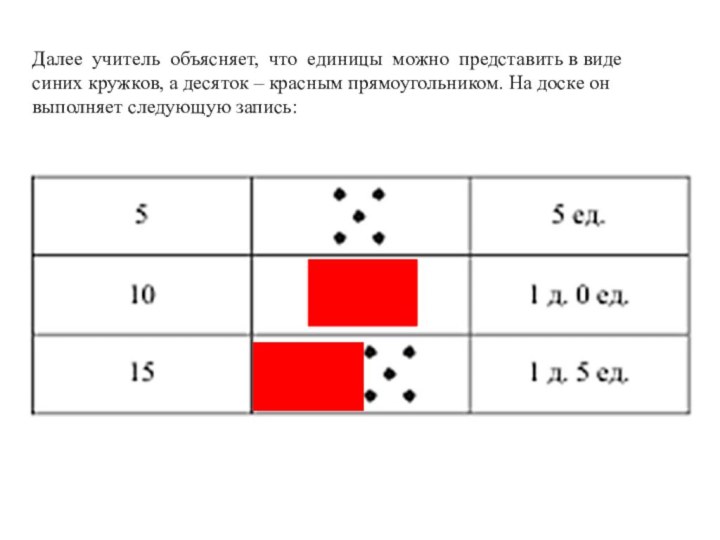
Слайд 20 Далее учитель объясняет, что единицы можно представить в
виде синих кружков, а десяток – красным прямоугольником. На
доске он выполняет следующую запись:Слайд 22 Графическая запись этих примеров выполняется учениками с помощью
цветных карандашей в тетради, либо с помощью подвижных прямоугольников
и кружков, вырезанных из картона на парте. Для слабых учащихся с обратной стороны красных прямоугольников можно сделать подсказку нарисовать десять синих кружков, которая им будет напоминать, что десять единиц – это один десяток.Далее учащимся предлагается анализировать числа по десятичному составу, без использования наименований десятков «дес.» и единиц «ед.» при числах.
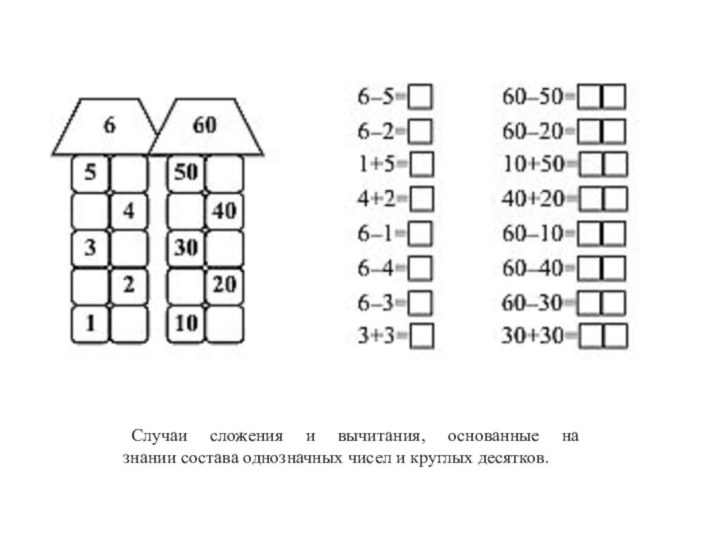
Слайд 24 Случаи сложения и вычитания, основанные на знании
состава однозначных чисел и круглых десятков.
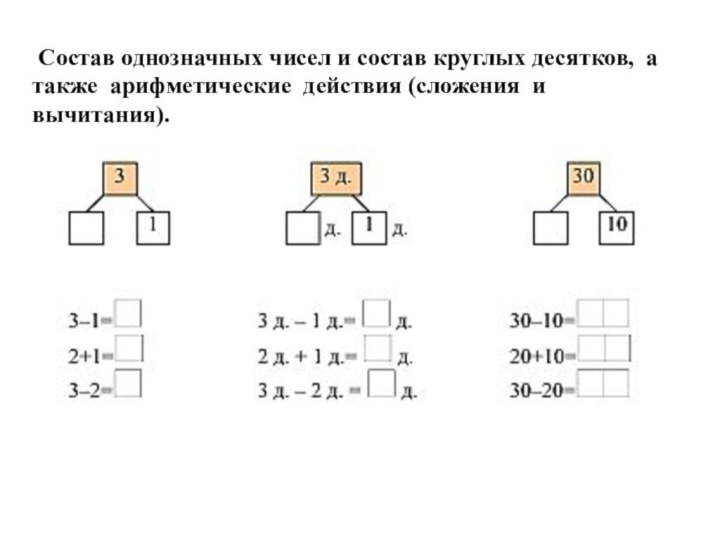
Слайд 25
Состав однозначных чисел и состав круглых десятков,
а также арифметические действия (сложения и вычитания).
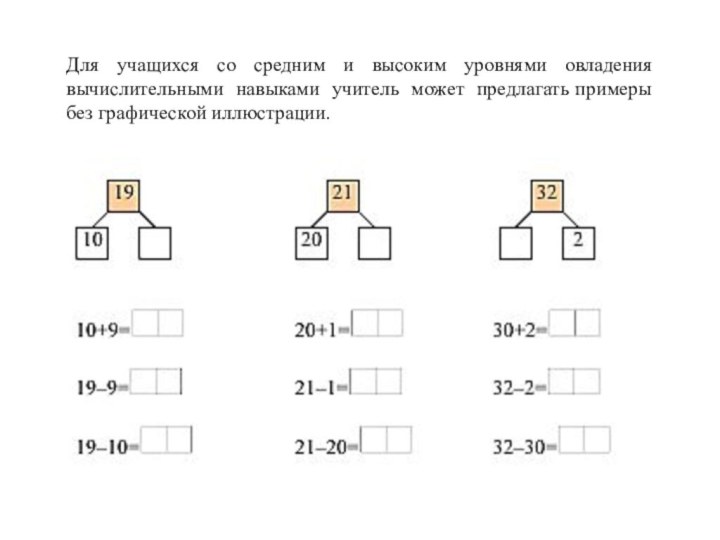
Слайд 27 Для учащихся со средним и высоким уровнями овладения
вычислительными навыками учитель может предлагать примеры без графической иллюстрации.
Слайд 29 Эта модель позволяет рассмотреть больше случаев сложения и
вычитания, основанных на знании десятичного состава двузначных чисел. При
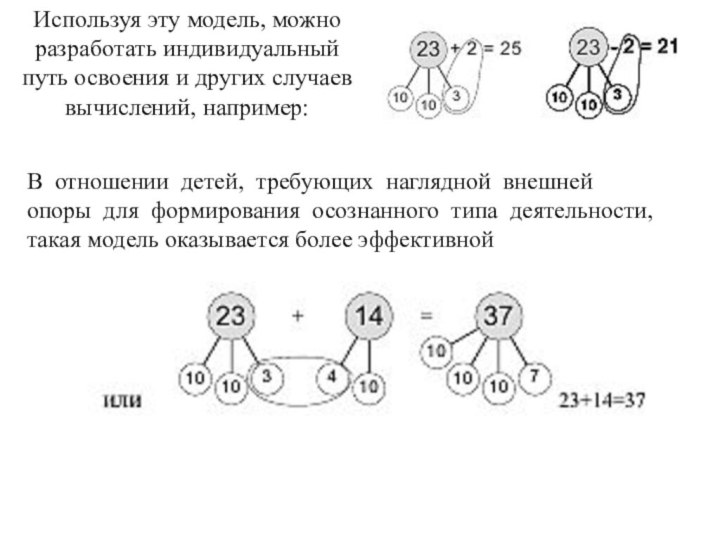
этом ребенок представляет суть приема на наглядном уровне, и, действуя руками (просто закрывая на модели пальцем или ладонью вычитаемое), сразу же проверяет правильность полученного ответа:Слайд 30 Используя эту модель, можно разработать индивидуальный путь
освоения и других случаев вычислений, например:
В отношении детей,
требующих наглядной внешней опоры для формирования осознанного типа деятельности,
такая модель оказывается более эффективной
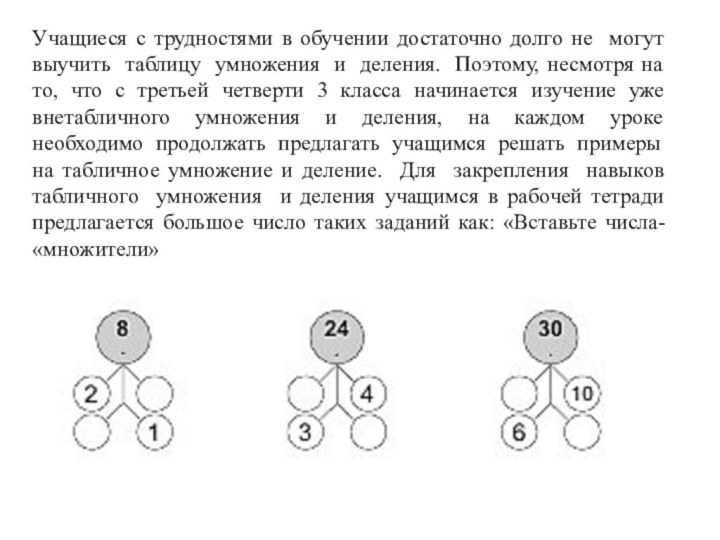
Слайд 32 Учащиеся с трудностями в обучении достаточно долго не
могут выучить таблицу умножения и деления. Поэтому, несмотря на
то, что с третьей четверти 3 класса начинается изучение уже внетабличного умножения и деления, на каждом уроке необходимо продолжать предлагать учащимся решать примеры на табличное умножение и деление. Для закрепления навыков табличного умножения и деления учащимся в рабочей тетради предлагается большое число таких заданий как: «Вставьте числа-«множители»
Слайд 34
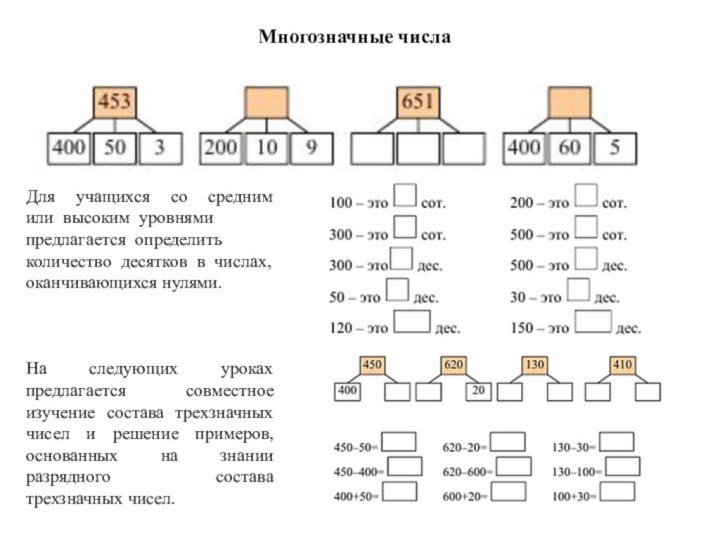
Многозначные числа
Для учащихся со средним или высоким
уровнями
предлагается определить количество десятков в числах,
оканчивающихся нулями.
На
следующих уроках предлагается совместное изучение состава трехзначных чисел и решение примеров, основанных на знании разрядного состава трехзначных чисел. Слайд 35 Для облегчения решения примеров на сложение и вычитание
чисел без перехода через разряд; сложение, когда в сумме
получаются круглые десятки; сложение и вычитание с переходом через разряд – учащимся с низким уровнем вычислительного навыка в рабочей тетради предлагается следующая запись примеров:
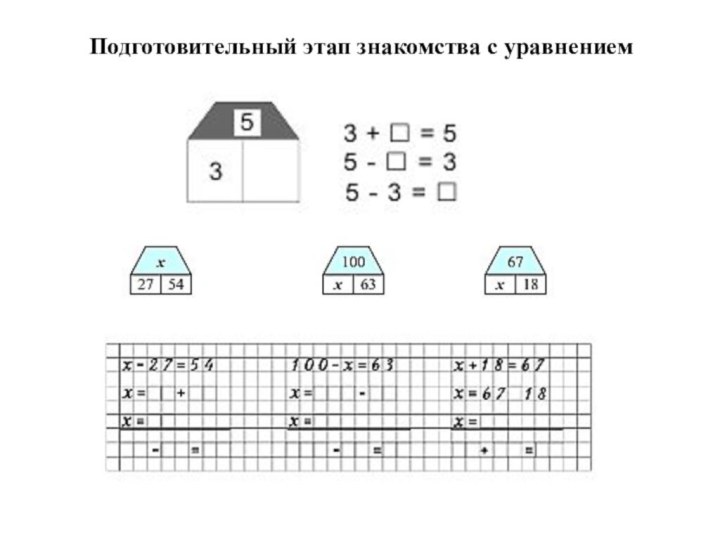
Слайд 37
Работа над задачами
Умением решать арифметические задачи, учащиеся
с проблемами в развитии овладевают с большим трудом –
это обусловлено в первую очередь особенностями мышления этих детей. Рекомендации для учителей при обучении решению арифметических задач учащихся с низким уровнем решения задач:1. Необходимо визуализировать содержание задачи, т.е. образно, зрительно дать возможность учащимся представить ту жизненную ситуацию, которая в ней отражена. Для того учитель иллюстрирует задачу (предметами, карточками с изображением этих предметов, чертежом, схемой, таблицей и пр.) или учащиеся сами могут нарисовать картинку, чтобы задача стала им понятней.
2. Необходимо больше времени предоставлять учащимся с низким уровнем решения задач на рассматривание визуальной информации.
3. Учащиеся с низким уровнем обязательно должны сами читать задачу вслух или шепотом, так называемым «жужжащим» чтением, но не «про себя».
Слайд 38 4.Учителю необходимо самому или с помощью сильных учеников
привести пример из жизни, где требуется такое же решение.
5. Перед решением задачи учащиеся обязательно должны проговорить последовательность своих действий, т.е. обязательно рассказать план решения задачи.
6. При решении задачи учитель также должен побуждать учащихся к вербализации выполняемых действий.
7. Учитель должен следить при записи решения задачи, чтобы учащиеся записывали его аккуратно, следили за строчками, чтобы они «не съезжали».
8. После решения задачи учителю необходимо предложить учащимся рассказать, как они решили задачу.
Слайд 39 Последовательность работы над усвоением содержания задачи с учащимися
с низким уровнем решения задач
(М.Н. Перова):
1. Работа
над содержанием задачи: а) разбор непонятных слов и выражений, встречающихся в задаче (до предъявления задачи);
б) чтение текста задачи учителем и учащимися;
в) запись условия задачи (иллюстрация задачи);
г) повторение задачи по вопросам;
д) воспроизведение одним из учащихся полного текста задачи.
Слайд 40
2. Поиск решения задачи.
3. Решение задачи.
4.
Запись решения.
5. Формулировка ответа.
6. Проверка решения
задачи: а) составление и решение обратной задачи;
б) установление соответствия между числами, полученными в результате решения задачи, и данными числами;
в) решение задачи другим способом;
г) прикидка ответа (установление соответствия искомого числа области своих значений);
Слайд 41
7. Последующая работа над решенной задачей:
а) изменение
отношений между данными условия задачи и выяснение, как это
изменение отразится на решении задачи;б) изменение вопроса задачи;
в) изменение условия задачи, привнесение в него
дополнительного данного или изъятие какого-либо данного;
г) изменение числовых данных, сюжета задачи, решение задачи, аналогичной данной.
Слайд 42 Иллюстрация задачи способствует обогащению у учащихся имеющихся представлений
о предметах и явлениях окружающей действительности, а также чувственного
опыта и пр. С опорой на иллюстрацию, учитель организует воспитательные беседы, проводит словарную работу, поясняет значение трудных слов, например: тюль, машинистка, закройщица, портниха, гончар, столяр, парник, электровоз, улья, заповедник, пекарня и пр.Слайд 43 Работа над трудными словами организуется ранее, например, на
этапе устного счета, когда учащимся предлагается расшифровать слово. Произведя
устные вычисления, и расшифровав слово, учащиеся поясняют его значение. Например, учащимся предлагается расшифровать слово, объяснить его значение.
Слайд 44
Используются основные виды иллюстраций:
1. Предметная иллюстрация (изображение
предметов,
о которых говорится в задаче.)
2. Схематическая иллюстрация
(краткая запись). Задача: На уроке труда 8 девочек вышили по 2 платочка каждая. Сколько всего … ? Закончи рисунок. Реши задачу.
Учащиеся самостоятельно дорисовывают по 2 платочка рядом с каждой девочкой и решают задачу.
Слайд 45 Задачи на деление по содержанию также удобно решать
с помощью предметной иллюстрации.
Задача: На уроке труда девочки
вышили 16 платочков. Каждая их них вышила по 2 платочка. Сколько девочек вышивало платочки? Слайд 46 Задача: Масса двух одинаковых чемоданов равна массе
двух одинаковых рюкзаков и сумки. Узнай массу чемодана, если
масса рюкзака 8 кг, а масса сумки 4 кг.Слайд 47 Среди схематических иллюстраций в рабочей тетради широко использованы
такие виды краткой записи как сокращенно-структурная, графическая и в
виде таблицы. Учащихся с низким уровнем овладения решением задач не обязательно обучать всем видам иллюстраций задач, достаточно обучить их только теми, которыми они часто будут пользоваться, и которые им доступны. Сокращенно-структурная форма записи, при которой каждая логическая часть задачи записывается с новой строки. Вопрос задачи записывается или внизу, или сбоку. Текст задачи принимает наглядно воспринимаемую форму.Задача: В авторемонтной мастерской 12 механиков, слесарей в 6 раз больше, чем механиков и 6 электриков. Сколько всего рабочих в авторемонтной мастерской?
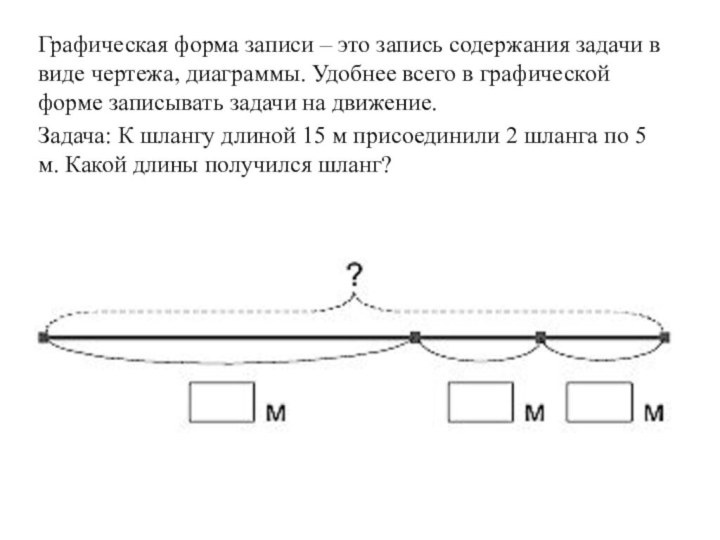
Слайд 48 Графическая форма записи – это запись содержания задачи
в виде чертежа, диаграммы. Удобнее всего в графической форме
записывать задачи на движение.Задача: К шлангу длиной 15 м присоединили 2 шланга по 5 м. Какой длины получился шланг?
Слайд 49 Так же достаточно широко используется в рабочей тетради
краткая запись содержания задачи в виде таблицы. Данный вид
иллюстрации используется чаще при решении задач на пропорциональную зависимость (на соотношение скорости, времени и пути; цены, количества и стоимости и др.).Задача: В одном куске было 24 м ткани, а в другом –на 8 м меньше. Из всей этой ткани сшили одинаковые платья, расходуя на каждое по 4 м ткани. Сколько сшили платьев?
Слайд 50
Большинство учащихся с низким уровнем нуждаются в
многократных повторениях (закреплениях) задач одного и того же типа.
Они с трудом переключаются на новый тип задач.Решение задач другого типа, как на уроке, так и дома не приводит к положительному результату. Таким образом, учащимся с низким уровнем усвоения математическими знаниями, умениями и навыками рекомендуется задавать на дом решение задач такого же типа, как они решали на уроке, учащимся же со средним или высоким уровнем можно задавать либо обратную данной или задачу другого типа.