Презентация на тему по математике Моделирование ситуаций при решении задач на движение

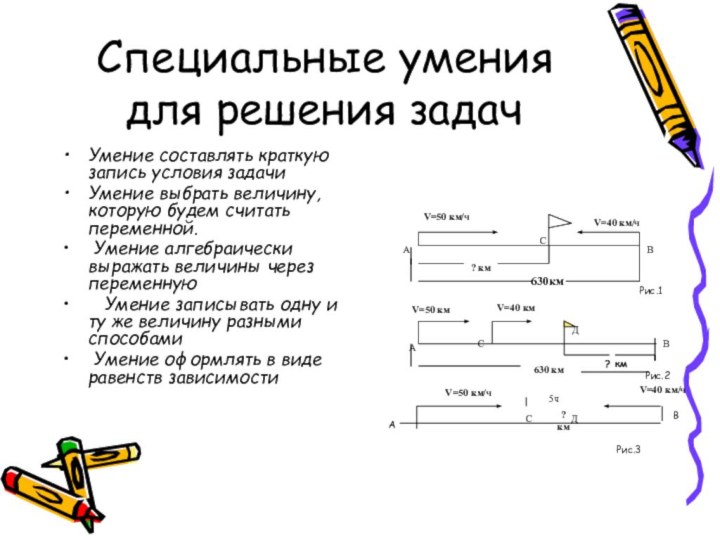
анализа текста задачи необходимо уметь выделить объекты, о которых

идёт речь в задаче, а также её условие и вопрос, установить известные, неизвестные и
искомые величины, выделить ситуации, описанные в задаче.


На этапе поиска плана решения понадобятся умения записывать функциональную зависимость между величинами из формул, составлять из заданной задачи
 

На этапе реализации плана важнейшим оказывается умение переводить зависимости между величинами на математический язык.

На этапе исследования приходится интерпретировать результат на языке данной задачи, выполнять проверку решения, оценивать его сточки зрения оптимальности.

Основным методом решения задач является метод с использованием уравнений 

условия задачи
Умение выбрать величину, которую будем считать переменной.
Умение

алгебраически выражать величины через переменную
   Умение записывать одну и ту же величину разными способами
 Умение оформлять в виде равенств зависимости

V=40 км/ч

630 км

А

В

С

А

В

С

Д

V=50 км/ч

V=40 км/ч

С

Д

5ч

?
км

V=50 км/ч

630км

V=50 км

V=40 км

? км

Рис.1

Рис.2

А

В

Рис.3

+ s2

в противоположных направлениях одновременно вышли два лыжника, один со

скоростью 14 км/ч, а другой со скоростью 13 км/ч Какое расстояние будет между лыжниками через 2 часа? ( см таблицу 2)
 

сёл одновременно выехали навстречу 2 всадника и встретились через

4 часа. Скорость одного из них 11 км/ч. Расстояние между сёлами 80 км. Найдите скорость другого всадника.

пункта в одном направлении одновременно выехали две машины. Скорость

первой машины 40 км/ч, а второй в 2 раза больше. Какое расстояние будет между ними через 2 часа?

двух пунктов, расстояние между которыми 210 км, вышли одновременно

навстречу друг другу два электропоезда. Скорость одного из них на 5 км /ч больше скорости другого. Найдите скорость каждого электропоезда, если они встретились через 2 часа после своего выхода.

течению реки, то его скорость равна собственной скорости катера

(в стоячей воде), увеличенной на скорость течения реки.
Если катер движется против течения реки, то его скорость равна собственной скорости катера, уменьшенной на скорость течения реки.

ней нужно заполнить пустые места, а для этого сформулировать

и решить устно четыре задачи на движение катера по реке.
 

катера при движении по течению реки равна 40 км/ч,

а при движении против течения она составляет 34 км/ч. Какова скорость течения реки?

Катер спустился вниз по реке к озеру. При этом за 2 ч он прошёл 60 км. По озеру он двигался 3ч со скоростью 28 км/ч, а потом поднялся по другой реке, которая впадает в то же озеро, за 4 ч. Узнайте путь, который прошёл катер за всё время движения, считая скорости течения рек одинаковыми

1. Из города А в город В выезжает велосипедист,

а через 3 ч после его выезда из города В навстречу ему выезжает мотоциклист, скорость которого в 3 раза больше, чем скорость велосипедиста. Велосипедист и мотоциклист встречаются на полпути между А и В. Если бы мотоциклист выехал не через 3ч, а через 2 ч после велосипедиста, то встреча произошла бы на 15 км ближе к городу А. Найти расстояние между А и В.

пункта А в пункт В выезжает объект «1, т.е

велосипедист, а через 3 ч из пункта В в пункт А выезжает объект №2 – мотоциклист, со скоростью в 3 раза большей, чем скорость велосипедиста. Они встречаются в середине пути между А и В .

Так как у обоих объектов длина пути одинакова и она равна половине пути, поэтому рациональнее половину пути обозначить через х.
Далее разговор ведётся о сравнении скоростей. А поэтому: скорость велосипедиста удобно обозначить через у км/ч, а скорость мотоциклиста - 3у км/ч.
Работа с неиспользованными данными (3 ч).
Выразить формулами время движения каждого объекта и записать в виде уравнения соотношениями между временем движения объекта№1 и временем движения объекта №2:

обсуждается аналогично, но теперь пройденные расстояния различны, приходится их

сравнивать

До встречи велосипедист проехал (х-15)км, мотоциклист (х+15) км, тогда велосипедист находился в пути ,
а мотоциклист .

Какой объект находился в пути больше? (велосипедист на 2 ч). Отсюда другое уравнение

система уравнений



Решение этой системы. Следует обратить внимание, что

х=90 – это половина пути. Ответ:180 км

рассуждений полезно составить таблицу.

Стандартная схема решения задач на движение состоит из трёх

этапов:
отбор неизвестных;
составление соотношений между этими неизвестными в виде уравнений, систем уравнений и неравенств;
решение уравнений, систем уравнений и неравенств.

Пешеход, велосипедист и мотоциклист двигались по шоссе в одну

сторону каждый со своей постоянной скоростью. В момент, когда пешеход и велосипедист находились в одной точке, мотоциклист отставал от них на 3 км. На сколько км велосипедист обогнал пешехода в тот момент, когда пешехода настиг мотоциклист?

Введём обозначения:
пусть скорость пешехода k (км/ч), скорость велосипедиста bk (км/ч),

скорость мотоциклиста ak (км/ч), где a, b, k - некоторые постоянные.

Пешеход и велосипедист находятся в одной точке. На рис.1

это точка B. Мотоциклист отстаёт на 6 км (то есть его можно поместить в точку А, которая находится левее точки В), АВ=6.

В

А

6 км

Мотоциклист догнал пешехода в некоторой точке, то есть они

оба переместились в точку С на рис.2, которая расположена правее точки В. В это момент велосипедист продвинулся дальше и находится на некотором расстоянии от них в точке Д. Расстояния ВС и СД неизвестны. Поэтому логично обозначить через х и у, т.е. ВС= х, СД= у..

А

В

С

Д

6км

Схема на рис. даёт возможность установить связи между величинами х, у и к, а, в. В самом деле, если пешеход прошёл х км со скоростью к км/ч, то значит, на путь от пункта В до С он затратил к/х ч.
Но тоже самое время находился в пути и мотоциклист, преодолевший расстояние от В до С и ещё от А до В, т.е.

х

у

Дальнейшее рассуждение
Но тоже самое время находился в пути и

велосипедист, который продвинулся от точки В до точки Д, т.е.

Итак, получены равенства

Исключим к в каждом из равенств:

х =

х =

А затем получим два способа представления неизвестной х

х =

(1)

х =

(2)

Приравниваем правые части выражений (1) и (2)

и получим, что

у =

(3)

Ситуация 3
Мотоциклист догнал велосипедиста в некоторой точке, находящейся правее

Д. Назовём её точкой Е, а в это время пешеход тоже продвинулся вперёд к некоторой точке Е. По условию расстояние от F до Е равно 3 км

А

В

С

F

E

Д

6 км

z

y

3 км

известно, что FE=3, но про длину отрезка BF ничего

не сказано. Обозначим эту величину через z. От пункта А до пункта Е мотоциклист преодолел расстояние 6+z+3=9+z (км) со скоростью ak км/ч, т.е. находился в пути

Но за это же время велосипедист проехал расстояние от пункта B до E,т.е. (z+3) км со скоростью bk км/ч, т.е.
z=

За то же самое время велосипедист проехал расстояние от пункта В до Е , т.е. (z+3) км со скоростью bk км/ч, т. е.

или

z=

(5)

Из уравнений (4) и (5) выразим а и в через z .

z =

a =

a = 1+

(6)

=

b=

1+

(7)
Подставим полученные значения а и в в равенство

(3.) и получим искомое значение у:

у =

Таким образом получили, что велосипедист обогнал пешехода на 2 км в тот момент, когда мотоциклист настиг пешехода.

Велосипедист отправляется из А в В и после 15-минутного

отдыха в пункте В возвращается в пункт А. На пути из А в В велосипедист догоняет в 11 часов пешехода, который движется из А в В со скоростью в 4 раза меньшей, чем у велосипедиста. Определить время отправления велосипедиста из пункта А, если известно, что велосипедист возвращается в пункт А одновременно с прибытием пешехода в пункт В.
Решение. Составим схематичные модели ситуаций, складывающихся в процессе движения велосипедиста и пешехода.
Пусть АС = а, ВС = в, у- скорость пешехода, х – время отправления велосипедиста из пункта А.

настиг пешехода в некоторой точке С между А и

В (рис. 4). Это значит, что расстояние АС велосипедист проехал за 11 – х часов со скоростью 4v.

А

В

С

а

b

Составим уравнение

Велосипедист и пешеход встретились в 12ч. В некоторой точке

Д, расположенной между пунктами С и В, когда велосипедист возвращается в А из В. Длину отрезка СД обозначим через с, а длину отрезка ДВ – черезd

А

С

Д

В

12ч

11 ч

с

d

Итак, пешеход прошёл расстояние СД за 1 час со скоростью v. Значит c/v=1→ c=v. За это же время, т.е. за 1 час велосипедист преодолел расстояние в + d. Поскольку b = c +d, запишем, что в +d = c + d. С учётом 15 мин.
(15 = 1/4 ч), потраченных велосипедистом на отдых, составим уравнение:

установлено, что c =v , тогда





1+


d=c.
Т.е.

СД = ДВ. Поскольку расстояние между пунктами С и Д пешеход одолел за 1 час, столько же времени ему потребуется на путь от В до Д,
т.е. 1 час.