- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Материал к проведению недели математики в старших классах
Содержание
- 2. Содержание: Из биографии математиковТестПоэтические страницы
- 3. ГеронДиофантАль-Хорезми МухаммедЕвклидОмар ХайямФалесВиетПифагорАрхимедДекартЛобачевскийКовалевскаяИз биографии математиков прошлого
- 4. Герон Александрийский(гг. рождения и смерти неизвестны, вероятно, I в.)
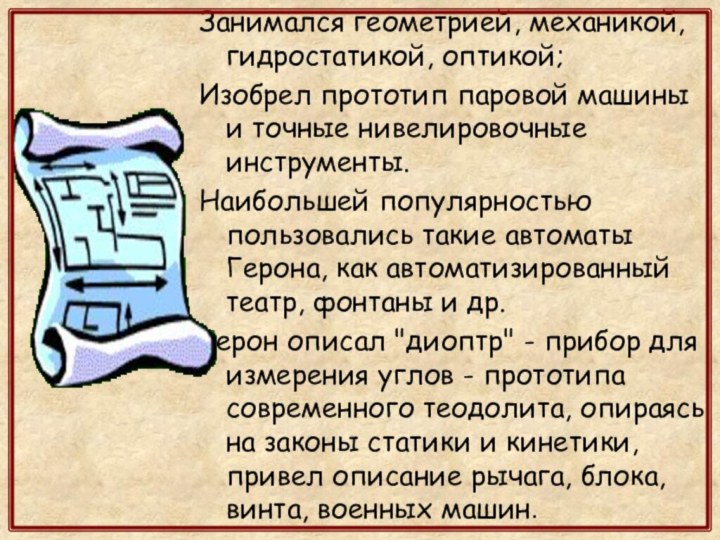
- 5. Занимался геометрией, механикой, гидростатикой, оптикой;Изобрел прототип паровой
- 6. В оптике сформулировал законы отражения света,
- 7. Знаменитая "Формула Герона" для площади треугольника
- 8. Диофант из Александрии(гг. рождения и смерти неизвестны, вероятно, 200/214 - 284/298 гг.)
- 9. Древнегреческий математик из Александрии. В одной из
- 10. Диофант автор трактата Арифметика в 13 книгах
- 11. Аль-Хорезми Мухаммед бен-Муса(783-850 г.г.)
- 12. Аль-Хорезми родился в Средней Азии, г.Хива, территория
- 13. Его работа Algoritmi de numero Indorum
- 14. Аль-Хорезми также издал астрономические и тригонометрические таблицы.Используя
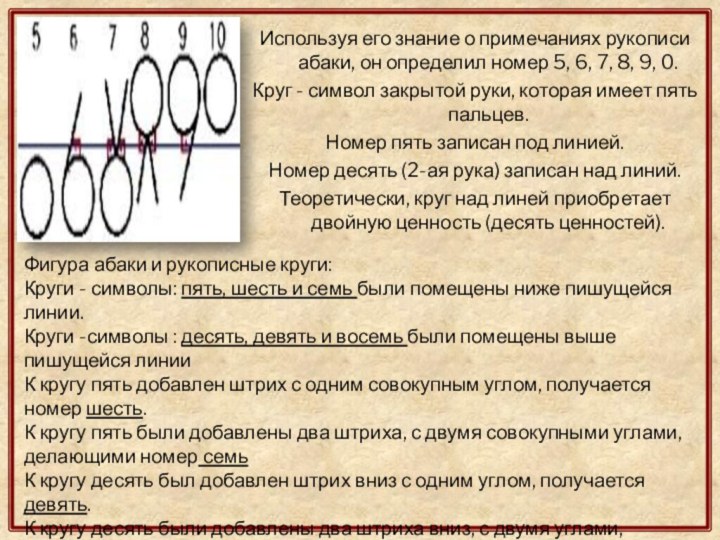
- 15. Используя его знание о примечаниях рукописи абаки,
- 16. Эволюция записи чисел по Хорезми
- 17. ЕвклидГоды жизни 365-300 гг. до. н. э.)
- 18. Древнегреческий математик, автор первого трактата по геометрии.Эта
- 19. В "Началах" Евклид дает строгое и логическое
- 20. Евклид, как и другие великие греческие геометры,занимался
- 21. Фрагмент старейшего папируса с диаграммами из "Элементы
- 22. Омар ХайямГоды жизни1048-1131гг.
- 23. Омар Хайям - (полное имя Гияс ад-дин
- 25. Список математическихтрактатов Омара Хайяма Трудности арифметики (Мушкилат
- 26. Омар Хайям вошел в историю
- 27. Вот одно из стихотворений Омара: Чтоб
- 28. Фалес МилетскийГоды жизни625 – 548 гг. до н.э.
- 29. Фалес Милетский имел титул одного
- 30. Фалесу Милетскому приписывают простой
- 31. Доказал знаменитую теорему, которую назвали теоремой Фалеса:Если
- 32. Франсуа ВиетГоды жизни1540 -1603
- 33. Франсуа Виет родился в Fontenay-le-Comte,
- 34. Теорема ВиетаПо праву достойна в стихах быть
- 35. ПифагорГоды жизни580 – 500 гг.до н.э.
- 36. Родился на острове Самос около 580 г.
- 37. Вернувшись на родину, Пифагор организовал пифагорейский орден
- 38. Излюбленной геометрической фигурой пифагорейцев была пентаграмма или
- 39. Он был четыре раза подряд олимпийским чемпионом.В
- 40. АС²+ ВС²=АВ²ВСАОн доказал известную теоремуЕсли дан нам
- 41. Однако в настоящее время установлено, что эта
- 42. Пифагоровы штаны Пифагоровы штаны (школьн.,
- 43. Пребудет вечной истина, как скороЕё
- 44. Архимед из СиракузГоды жизни287 – 212 гг. до н.э.
- 45. Архимед родился
- 47. Архимед проверяет и создает теорию пяти механизмов,
- 48. Нет, не всегда смешон
- 49. Рене ДекартГоды жизни1596 – 1650 гг.
- 50. Биография Происходил из старинного дворянского
- 51. Математические исследования Декарта тесно связаны
- 52. Декартова система координат - система координат
- 53. Лобачевский Николай ИвановичГоды жизни1792 – 1856 гг.
- 54. Русский математик, создатель неевклидовой геометрии. Большой вклад
- 55. Высокий лоб, нахмуренные брови.
- 56. Софья КовалевскаяГоды жизнигг.
- 57. Математик должен быть поэтом в душе
- 58. Она бы с блеском могла
- 59. 30 января 1884 года Ковалевская прочитала первую
- 60. ВыходКакую теорему называют теоремой «невесты»Теорема ПифагораТеорема Ферма
- 61. МОЛОДЕЦ!Следующий вопрос
- 62. Ошибка!Вернемся к вопросу?
- 63. Выход«Математик должен быть поэтом в душе».(кто это сказал?)ПифагорЛобачевскийКовалевская
- 64. МОЛОДЕЦ!Следующий вопрос
- 65. Ошибка!Вернемся к вопросу?
- 66. ВыходГеометрия, которая изучается в школе, называется по
- 67. МОЛОДЕЦ!Следующий вопрос
- 68. Ошибка!Вернемся к вопросу?
- 69. ВыходНазовите ученого чьим именем названа следующая теорема:«В прямоугольном треугольнике квадрат гипотенузы равенсумме квадратов катетов»ПифагорОмар ХайямВиет
- 70. МОЛОДЕЦ!Следующий вопрос
- 71. Ошибка!Вернемся к вопросу?
- 72. ВыходУченый , который нашёл очень простое приближенное значениечисла п равное 22/7.АрхимедЕвклид
- 73. МОЛОДЕЦ!Следующий вопрос
- 74. Ошибка!Вернемся к вопросу?
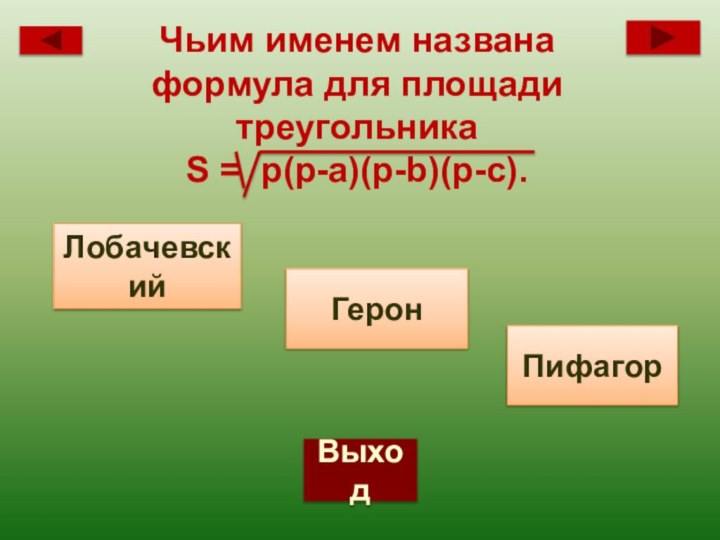
- 75. ВыходЧьим именем названа формула для площади треугольникаS = р(р-а)(р-b)(р-с).ЛобачевскийГеронПифагор
- 76. МОЛОДЕЦ!Следующий вопрос
- 77. Ошибка!Вернемся к вопросу?
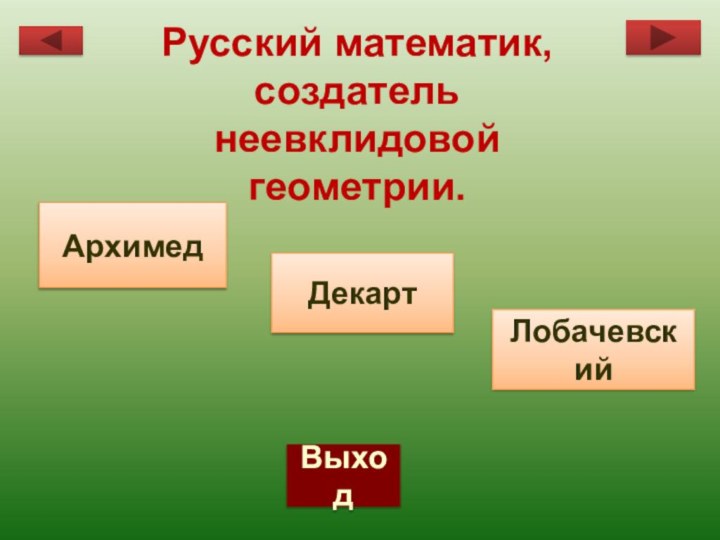
- 78. ВыходРусский математик, создатель неевклидовой геометрии.ДекартЛобачевскийАрхимед
- 79. МОЛОДЕЦ!Следующий вопрос
- 80. Ошибка!Вернемся к вопросу?
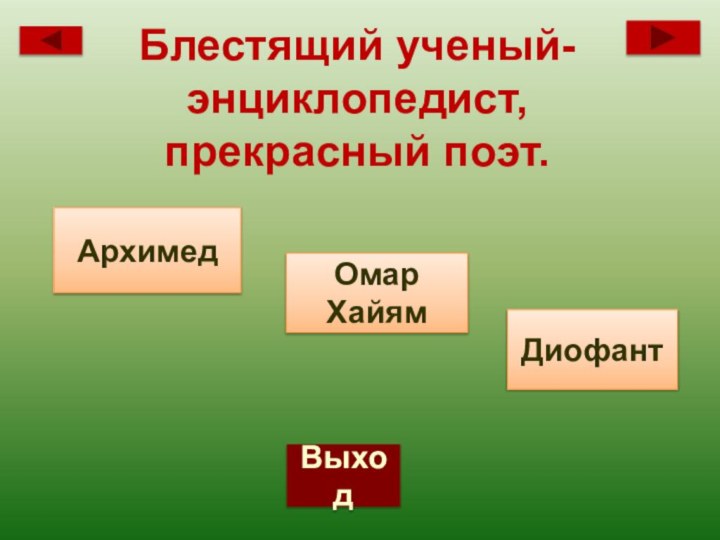
- 81. ВыходБлестящий ученый-энциклопедист, прекрасный поэт. ДиофантОмар ХайямАрхимед
- 82. МОЛОДЕЦ!Следующий вопрос
- 83. Ошибка!Вернемся к вопросу?
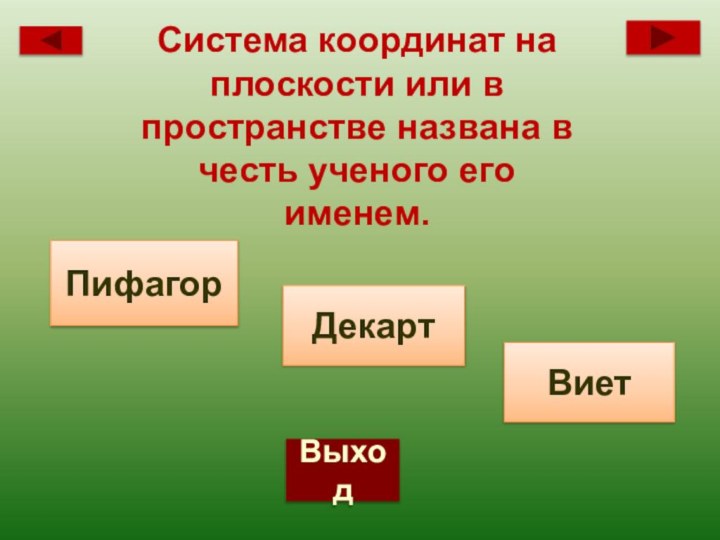
- 84. ВыходСистема координат на плоскости или в пространстве названа в честь ученого его именем.ДекартВиетПифагор
- 85. МОЛОДЕЦ!Следующий вопрос
- 86. Ошибка!Вернемся к вопросу?
- 87. ВыходЕго имя в видоизмененной форме превратилось в нарицательное слово "алгоритм".Омар ХайямДиофантАль-Хорезми
- 88. МОЛОДЕЦ!Следующий вопрос
- 89. Ошибка!Вернемся к вопросу?
- 90. Поэтические страницы
- 91. Хорошо, если платье твое без
- 92. Закон Архимеда Жил в Сиракузах
- 93. Теорема ПифагораЕсли дан нам треугольникИ при том
- 94. Скачать презентацию
- 95. Похожие презентации















































































Слайд 3
Герон
Диофант
Аль-Хорезми Мухаммед
Евклид
Омар Хайям
Фалес
Виет
Пифагор
Архимед
Декарт
Лобачевский
Ковалевская
Из биографии математиков прошлого
Слайд 5
Занимался геометрией, механикой, гидростатикой, оптикой;
Изобрел прототип паровой машины
и точные нивелировочные инструменты.
Наибольшей популярностью пользовались такие автоматы Герона,
как автоматизированный театр, фонтаны и др. Герон описал "диоптр" - прибор для измерения углов - прототипа современного теодолита, опираясь на законы статики и кинетики, привел описание рычага, блока, винта, военных машин.
Слайд 6 В оптике сформулировал законы отражения света, в
математике - способы измерения важнейших геометрических фигур.
Из его
работ известны "Механика", "Книга о подъемных механизмах", "Пневматика", "Книга о военных машинах", "Театр автоматов", "Метрика". В лучшей из них - "Метрике" даны определение шарового сегмента, тора, правила и формулы для точного и приближенного вычисления площадей правильных многоугольников, объемов усеченных конуса и пирамиды; даются правила численного решения квадратных уравнений и приближенного извлечения квадратных и кубических корней.
Слайд 7
Знаменитая "Формула Герона" для площади треугольника
,где р=(а+в+с)/2.
S=√p(p-a)(p-b)(p-c)
S=√p(p-a)(p-b)(p-c)
Слайд 9
Древнегреческий математик
из Александрии.
В одной из эпиграмм
Палатинской антологии
говорится:
Прах Диофанта гробница покоит дивись ей -
и камень.Мудрым искусством его скажет усопшего век.
Волей богов шестую часть жизни он прожил ребенком,
И половину шестой встретил с пушком на щеках.
Только минула седьмая, подружкою он обручился.
С ней пять лет проведя, сына дождался мудрец.
Только полжизни отцовской возлюбленный сын его прожил.
Отнят он был у отца ранней могилой своей.
Дважды два года родитель оплакивал тяжкое горе.
Тут и увидел предел жизни печальной своей.
Слайд 10 Диофант автор трактата Арифметика в 13 книгах (уцелели
только шесть книг) , посвященного главным образом исследованию неопределенных
уравнений (т.е. диофантовых уравнений).ДИОФАНТОВЫ УРАВНЕНИЯ - алгебраические уравнения или их системы с целыми коэффициентами, имеющие число неизвестных, превосходящее число уравнений, и у которых разыскиваются целые или рациональные решения.
ДИОФАНТОВЫ ПРИБЛИЖЕНИЯ - раздел теории чисел, изучающий приближения действительных чисел рациональными и вопросы, связанные с решением в целых числах линейных и нелинейных неравенств с действительными коэффициентами.
Слайд 12 Аль-Хорезми родился в Средней Азии, г.Хива, территория современного
Узбекистана.
Возглавлял в Багдаде библиотеку Дома мудрости, своего рода
Багдадской академии, при халифе ал-Мамуне. При другом халифе ал-Васике, преемнике ал-Мамуна, он возглавлял экспедицию к хазарам.
Как ученый Ал-Хорезми становится известным из его достижений в математике.
Имя аль-Хорезми в видоизмененной форме Algorithmus превратилось в нарицательное слово "алгоритм" и сначала означало всю систему десятичной позиционной арифметики
Слайд 13
Его работа
Algoritmi de numero Indorum
("Ал-Хорезми
о индийских числах")
дала название начало математическому термину "арифметика".
Другая
работа Ал-Хорезми, «Kitab al-jabr wa l-muqabala»(«Книга Интеграции и Уравнения») была синтезом индийской алгебры и греческой геометрии и имела самое глубокое влияние на развитие науки.
Слайд 14
Аль-Хорезми также издал астрономические и тригонометрические таблицы.
Используя примечания
абаки, Ал-Хорезми развивал систему рукописного десятичного числа.
Основанный на
углах, он определил номер 1, 2, 3 и 4. Арабские 1-2-3-4 числа форматируют на наличии углов:
Номер один (1) имеет один угол.
Номер два (2) имеет два угла.
Номер три (3) имеет три угла.
Номер четыре (4) имеет четыре совокупных угла.
Номер четыре закрыт из-за рукописной руки, пишут.
Слайд 15 Используя его знание о примечаниях рукописи абаки, он
определил номер 5, 6, 7, 8, 9, 0.
Круг -
символ закрытой руки, которая имеет пять пальцев. Номер пять записан под линией.
Номер десять (2-ая рука) записан над линий.
Теоретически, круг над линей приобретает двойную ценность (десять ценностей).
Фигура абаки и рукописные круги:
Круги - символы: пять, шесть и семь были помещены ниже пишущейся линии.
Круги -символы : десять, девять и восемь были помещены выше пишущейся линии
К кругу пять добавлен штрих с одним совокупным углом, получается номер шесть.
К кругу пять были добавлены два штриха, с двумя совокупными углами, делающими номер семь
К кругу десять был добавлен штрих вниз с одним углом, получается девять.
К кругу десять были добавлены два штриха вниз, с двумя углами, уменьшающие до номера восемь.
Слайд 18
Древнегреческий математик, автор первого трактата по геометрии.
Эта удивительная
книга пережила более двух тысячелетий.
Созданная там система евклидовой геометрии
и теперь изучается во всех школах мира и лежит в основе почти всей практической деятельности людей. Как-то царь Птолемей I спросил Евклида, нет ли более короткого пути для изучения геометрии, чем штудирование "Начал". На это Евклид смело ответил, что «В геометрии нет царской дороги".
Слайд 19 В "Началах" Евклид дает строгое и логическое изложение
всего геометрического материала, известного до него и дополненного им
самим. Это изложение строится на дедуктивном методе: в основу положены некоторые определения и истины, принимаемые без доказательств, а все дальнейшие утверждения строго доказываются на основании этих истин, или предложений, полученных из них."Начала" представляют большой труд, состоящий из 13 книг. Первые четыре книги содержат планиметрию, в них излагаются свойства плоских фигур, многоугольников и круга; пятая содержит теорию пропорций; шестая посвящена вопросам подобия фигур. Основные вопросы арифметики нашли свое место в седьмой, восьмой и девятой книгах; десятая содержит выяснение понятий о соизмеримых и несоизмеримых количествах; в одиннадцатой, двенадцатой и тринадцатой книгах изложены основные теоремы стереометрии.
«Начала»
Слайд 20
Евклид, как и другие великие греческие геометры,
занимался астрономией
("Феномены" ), оптикой
("Оптика" )и теорией музыки ("Сечение канона" ).
Это были первые прообразы будущих исследований по
математической физике. На геометрии Евклида
базируется классическая механика, ее апофеозом
было появление в 1687 г. «Математических начал
натуральной философии Ньютона», где законы земной
и небесной механики и физики устанавливаются в
абсолютном евклидовом пространстве.
Слайд 21 Фрагмент старейшего папируса с диаграммами из "Элементы геометрии"
Евклида
Papyrus found among the remarkable rubbish piles of Oxyrhynchus
in 1896-97 by the renowned expedition of B. P. Grenfell and A. S. Hunt. It is now located at the University of PennsylvaniaСлайд 23 Омар Хайям - (полное имя Гияс ад-дин Фатх
ибн Ибрахим Омар Хайям Нишапури) родился в Хорасане
(г.
Нишапур) - область, расположенная к востоку и юго-востоку от Каспийского моря. Известные нам математические результаты Хайяма относятся к трем направлениям: к алгебре, к теории параллельных, к теории отношений и учению о числе.
Слайд 24
Учился Хайям в Нишапуре, а затем в
крупнейших центрах науки того
времени, в Балхе и Самарканде, где
написал трактат "О доказательствах
задач алгебры и алмукабалы
На богатом историческом материале исследователи
доказали заслуги Омара Хайяма как ученого, который
сделал ряд важнейших открытий в области астрономии,
математики и физики.
С 1074 года Хайям возглавлял крупнейшую
астрономическую обсерваторию.
В середине 90-х г.г. XI века совершил
паломничество в Мекку. Последние
годы жизни Хайям провел в Нишапуре.
Слайд 25
Список математических
трактатов Омара Хайяма
Трудности арифметики (Мушкилат ал-хисаб)
- Местонахождение рукописи не найдено;
Алгебраический трактат без названия
- Тегеран;Трактат о доказательствах задач алгебры и алмукабалы (Риала фи-л-барахин 'ала маса'ил алджабр ва-л-мукабала) - Париж, Лейден, Лондон, Нью-Йорк, Рим;
Комментарии к трудностям во введениях книги Евклида (Шарх ма ашкала мин мусадарат китаб Уклидис) - Лейден.
Слайд 26 Омар Хайям вошел в историю всемирной
культуры не только как блестящий ученый-энциклопедист, но и как
прекрасный поэт, который воспевал свободу, бичевал ханжество и лицемерие, высмеивал суеверия. Его стихи были переведены на все языки мира.
Слайд 27
Вот одно из стихотворений Омара:
Чтоб мудро жизнь прожить,
знать надобно надо немало.
Два важных правила запомни для начала.
Ты
лучше голодай, чем что попало есть,И лучше будь один, чем вместе с кем попало.
Слайд 29 Фалес Милетский имел титул одного из
семи мудрецов Греции, он был поистине первым философом, первым
математиком, астрономом и, вообще, первым по всем наукам в Греции. Он был то же для Греции, что Ломоносов для России.Слайд 30 Фалесу Милетскому приписывают простой способ
определения высоты пирамиды. В солнечный день он поставил свой
посох там, где оканчивалась тень от пирамиды. Затем он показал, что как длина одной тени относится к длине другой тени, так и высота пирамиды относится к высоте посоха.
Слайд 31
Доказал знаменитую теорему, которую назвали теоремой Фалеса:
Если параллельные
прямые, пересекающие стороны угла, отсекают на одной его стороне
равные отрезки, то они отсекают равные отрезки и на другой его сторонеСлайд 33 Франсуа Виет родился в Fontenay-le-Comte, провинция
Vendee (Франция) в 1540 году. Отец Этьен Виет -
адвокат, мать Маргарита Дюпон. Виет имел возможность получить хорошее образование и относился к обучению очень серьезно. Став юристомпродолжал заниматься
математикой, астрономией
и космологией. В 1571 году
начал публиковать
Математический Канон с
Приложением на Тригонометриию
Слайд 34
Теорема Виета
По праву достойна в стихах быть воспета
О
свойствах корней теорема Виета.
Что лучше, скажи, постоянства такого:
Умножишь ты
корни – и дробь уже готова:В числителе «с», в знаменателе «а»,
А сумма корней тоже дроби равна.
Хоть с минусом дробь эта., что за беда-
В числителе «в», в знаменателе «а».
х + px + q=0
x1+x2=-p;
x1*x2=q;
2
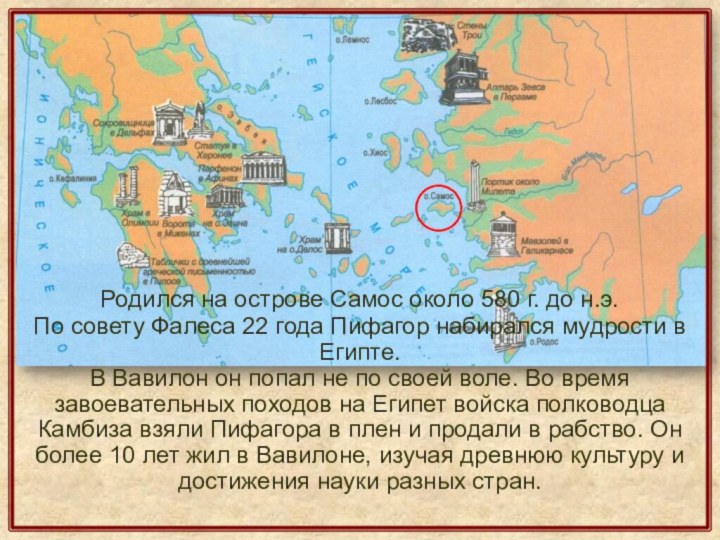
Слайд 36 Родился на острове Самос около 580 г. до
н.э.
По совету Фалеса 22 года Пифагор набирался мудрости в
Египте. В Вавилон он попал не по своей воле. Во время завоевательных походов на Египет войска полководца Камбиза взяли Пифагора в плен и продали в рабство. Он более 10 лет жил в Вавилоне, изучая древнюю культуру и достижения науки разных стран.
Слайд 37 Вернувшись на родину, Пифагор организовал пифагорейский орден и
школу философов и математиков.
Туда принимались с большими церемониями
после долгих испытанийВ школе существовал декрет, по которому авторство всех математических работ приписывалось самому Пифагору.
В школе была очень серьёзная дисциплина. Главным безоговорочным аргументом в научных спорах были слова «сам сказал». После этого дискуссии прекращались.
Слайд 38 Излюбленной геометрической фигурой пифагорейцев была пентаграмма или пифагорейская
звезда.
При встрече они рисовали её на песке, тем самым
приветствуя друг друга.Пентаграмма служила им паролем и была символом здоровья и счастья.
Слайд 39
Он был четыре раза подряд олимпийским чемпионом.
В пятисотых
годах до нашей эры Пифагор был убит в уличной
схватке во время народного восстания.После смерти его ученики окружили имя своего учителя множеством легенд, так, что правду о Пифагоре установить невозможно.
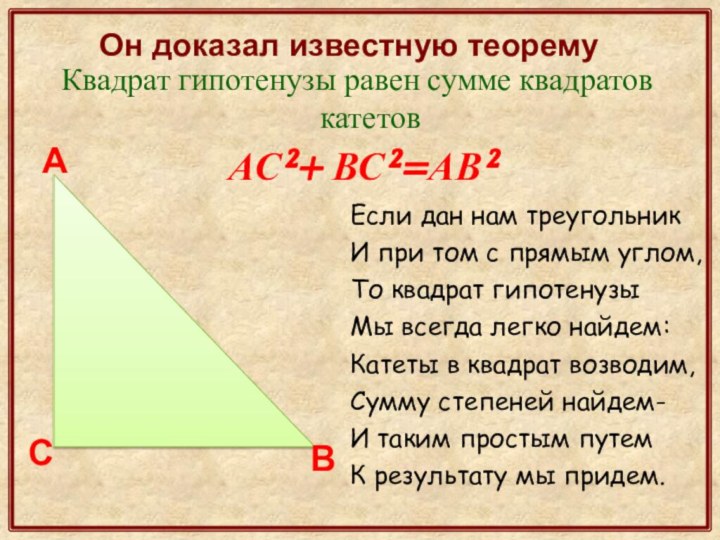
Слайд 40
АС²+ ВС²=АВ²
В
С
А
Он доказал известную теорему
Если дан нам треугольник
И
при том с прямым углом,
То квадрат гипотенузы
Мы всегда легко
найдем:Катеты в квадрат возводим,
Сумму степеней найдем-
И таким простым путем
К результату мы придем.
Квадрат гипотенузы равен сумме квадратов катетов
Слайд 41 Однако в настоящее время установлено, что эта важнейшая
теорема встречается в вавилонских текстах, написанных за 1200 лет
до Пифагора.Верёвочным треугольником со сторонами 3, 4 и 5 единиц пользовались ещё в Древнем Египте для построения прямых углов на местности.
Поэтому треугольник со сторонами 3, 4 и 5 называют ещё иногда египетским.
Слайд 42
Пифагоровы штаны
Пифагоровы штаны
(школьн., устар.)
- шуточное название теоремы Пифагора, возникшее в силу того,
что раньше в школьных учебниках эта теорема доказывалась через доказательство равенства суммы площадей квадратов, построенных на катетах прямоугольного треугольника, площади квадрата, построенного на гипотенузе этого треугольника.
Слайд 43
Пребудет вечной истина, как скоро
Её познает
слабый человек!
И ныне теорема Пифагора
Верна, как и в
его далёкий век.Обильно было жертвоприношенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, её почуя, вслед.
Они не в силах свету помешать,
А могут лишь, закрыв глаза, дрожать
От страха, что вселил в них Пифагор.
Слайд 45 Архимед родился в
287 году до нашей
эры в греческом городе Сиракузы,
где и прожил почти всю свою жизнь.Архимед-вершина научной мысли
древнего мира. Древнегреческий
математик, механик, военный инженер.
Последующие
ученые - Герон Александрийский
(1-11 вв. до н. э.), Папп Александрийский
(III в. н. э.) - мало что прибавили
к наследию Архимеда.
После учебы в Александрии Архимед
вновь вернулся в Сиракузы и унаследовал
должность придворного астронома.
Слайд 46
Основные
работы Архимеда касалисьразличных практических приложений
математики (геометрии), физики,
гидростатики и механики. В сочинении
"Параболы квадратуры" Архимед обосновал метод расчета площади параболического сегмента, причем сделал это за две тысячи лет до открытия интегрального исчисления. В труде "Об измерении круга" Архимед впервые вычислил число "пи" - отношение длины окружности к диаметру - и доказал, что оно одинаково для любого круга.
Слайд 47 Архимед проверяет и создает теорию пяти механизмов, известных
в его время и именуемых "простые механизмы". Это -
рычаг ("Дайте мне точку опоры, - говорил Архимед, - и я сдвину Землю"), клин, блок, бесконечный винт и лебедка. Изобретение бесконечного винта привело его к изобретению болта, сконструированного из винта и гайки.Слайд 48 Нет, не всегда смешон и
узок
Мудрец, глухой к делам земли:
Уже на рейдах в СиракузахСтояли римлян корабли.
Над математиком курчавым
Солдат занес короткий нож,
А он на отмели песчаной
Окружность вписывал в чертеж,
Ах, если б смерть – лихую гостью-
Мне так же встретить повезло,
Как Архимед, чертивший тростью
В минуту гибели – число!
(Д.Кедрин)
Слайд 50
Биография
Происходил из старинного дворянского рода.
Образование получил в иезуитской школе Ла Флеш в Анжу.
В начале Тридцатилетней войны служил в армии, которую оставил в 1621; после нескольких лет путешествий переселился в Нидерланды (1629), где провёл двадцать лет в уединённых научных занятиях. Здесь вышли его главные сочинения - "Рассуждение о методе, чтобы верно направлять свой разум и отыскивать истину в науках" (1637, рус. пер. 1953), "Размышления о первой философии..." (1641, рус. пер. 1950), "Начала философии" (1644, рус. пер. 1950). В 1649 по приглашению шведской королевы Кристины переселился в Стокгольм, где вскоре умер.Слайд 51 Математические исследования Декарта тесно связаны с
его работами по философии и физике. В "Геометрии" (1637)
Декарт впервые ввёл понятия переменной величины и функции.
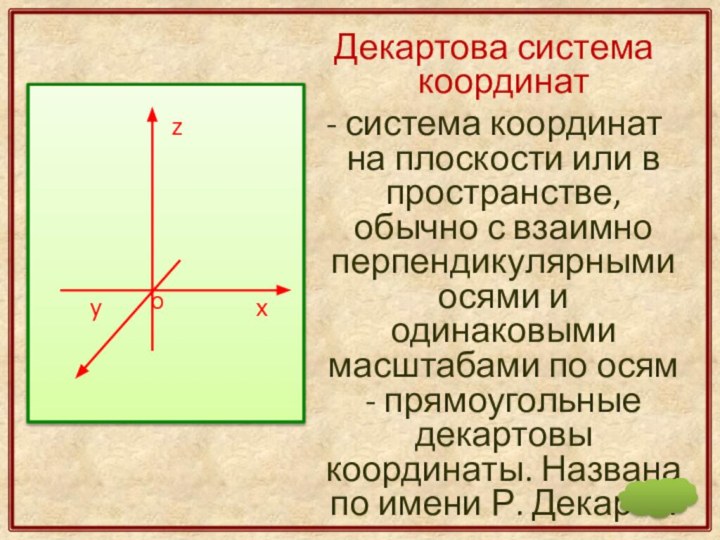
Слайд 52
Декартова система координат
- система координат на
плоскости или в пространстве, обычно с взаимно перпендикулярными осями
и одинаковыми масштабами по осям - прямоугольные декартовы координаты. Названа по имени Р. Декарта.Слайд 54 Русский математик, создатель неевклидовой геометрии. Большой вклад
внес в математический анализ и алгебру. Он разработал метод
приближенного решения алгебраических уравнений высших степеней.Главным достижением Лобачевского является доказательство того, что существует более чем одна «истинная» геометрия.
Среди опубликованных работ ученого – О началах геометрии (1829–1830), Воображаемая геометрия (1835), Применение воображаемой геометрии к некоторым интегралам (1836), Новые начала геометрии с полной теорией параллельных (1835–1838), Геометрические исследования по теории параллельных линий (1840).
Слайд 55
Высокий лоб, нахмуренные брови.
В
холодной бронзе – отраженный луч…
Но, даже неподвижный
и суровый,Он, как живой, -спокоен и могуч…
Пусть новых линий не начертят руки,
Он здесь стоит, взнесенный высоко,
Как утверждение бессмертья своего,
Как вечный символ торжества науки.
Слайд 57 Математик должен быть поэтом в душе
С. Ковалевская
Об отношениях и связях с предками Ковалевская говорила, что получила в наследство страсть к науке от прапрапрадеда, венгерского короля Матвея Корвина; любовь к математике, музыке и поэзии - от деда матери с отцовской стороны, астронома Шуберта; личную любовь к свободе - от Польши; от цыганки прабабки - любовь к бродяжничеству и неуменье подчиняться принятым обычаям. Остальное - от России.
Слайд 58 Она бы с блеском могла поступить
в любой российский университет, но не поступила. Пол был
не тот, и на этом "гендерном" основании в высшие учебные заведения девушек не принимали. Отец тоже имел серьезные предубеждения против "ученых женщин". Оставалось одно: уехать учиться за границу.Слайд 59 30 января 1884 года Ковалевская прочитала первую лекцию
в Стокгольмском университете. 24 июня того же года она
была официально извещена, что "назначена профессором сроком на пять лет".Через четыре года, 6 декабря 1888 года, Парижская академия присудила ей престижную премию Бордена. Следующая, шведская премия короля Оскара II состояла из 1500 крон и повышения в звании среди друзей. Они теперь называли ее "профессор Соня».
Она была первой женщиной-математиком, доктором философии. Ей принадлежит роман «Нигилистка»
Слайд 66
Выход
Геометрия, которая изучается в школе, называется по имени
ученого,
создавшего руководство по математике под названием «Начала».
Назовите этого учёного.
Герон
Диофант
Евклид
Слайд 69
Выход
Назовите ученого чьим именем названа следующая теорема:
«В прямоугольном
треугольнике квадрат гипотенузы равен
сумме квадратов катетов»
Пифагор
Омар Хайям
Виет
Слайд 72
Выход
Ученый , который нашёл очень простое приближенное значение
числа
п равное 22/7.
Архимед
Евклид
Слайд 75
Выход
Чьим именем названа формула для площади треугольника
S =
р(р-а)(р-b)(р-с).
Лобачевский
Герон
Пифагор
Слайд 84
Выход
Система координат на плоскости или в пространстве названа
в честь ученого его именем.
Декарт
Виет
Пифагор
Слайд 87
Выход
Его имя в видоизмененной форме превратилось в нарицательное
слово "алгоритм".
Омар Хайям
Диофант
Аль-Хорезми
Слайд 91
Хорошо, если платье твое без прорех.
И о хлебе насущном подумать не грех.
А всего остального и даром не надо –Жизнь дороже богатства и почестей всех…
В этом мире глупцов, подлецов, торгашей
Уши, мудрый заткни, рот надежно зашей,
Веки плотно зажмурь – хоть немного подумай
О сохранности глаз, языка и ушей…
Книга жизни моей перелистана. Жаль!
От весны, от веселья осталась печаль.
Юность – птица: не помню, когда прилетела
И когда улетела легкокрылая вдаль…
Я познание сделал своим ремеслом,
Я знаком с высшей правдой и низменном злом.
Все тугие узлы я распутал на свете
Кроме смерти, завязанной мертвом узлом…
Омар Хайям. «Рубли»
Слайд 92
Закон Архимеда
Жил в Сиракузах мудрец Архимед.
Был другом царя Гиерона.
Какой для царя самый
важный предмет?Вы все догадались корона!
Захотелось Гиерону сделать новую корону.
Золото отмерил строго.
Взял не мало и не много-
Сколько нужно-в самый раз.
Ювелиру дал заказ.
Через месяц Гиерону ювелир принес корону
И царю узнать охота: честно ль сделана работа?
Вот корона, Архимед, Золотая или нет?
И задумался ученый:
Как узнать состав короны?
И однажды, в ванне моясь, Погрузился он по пояс
На пол вылилась вода: догадался он тогда,
И помчался к Гиерону не обут и не одет…
-Эврика! Раскрыл секрет1
Пусть весы сюда несут и с водой большой сосуд…
На весы кладем корону и теперь такой же ровно
Ищем слиток золотой.
Мы теперь корону нашу опускаем в эту чашу.
Гиерон! Смотри сюда-
В чаше поднялась вода1
Ставлю черточку по краю,
А корону вынимаю.
В воду золото опустим.
В воду золото допустим…
Поднялась опять вода.
Метку ставлю я. Куда7
-Эврика! Раскрыл секрет1
Пусть весы сюда несут и с водой большой сосуд…
На весы кладем корону и теперь такой же ровно
Ищем слиток золотой.
Мы теперь корону нашу опускаем в эту чашу.
Гиерон! Смотри сюда-
В чаше поднялась вода1
Ставлю черточку по краю,
А корону вынимаю.
В воду золото опустим.
В воду золото допустим…
Поднялась опять вода.
Метку ставлю я. Куда7
Ну, конечно же, по краю.
-Ничего не понимаю.
Лишь две черточки я вижу.
Эта-выше, Эта – ниже.
Но какой же вывод главный?
Равный вес. Объем – не равный!
Понимаешь, Гиерон, я сейчас открыл закон.
Тот закон совсем простой:
Тело вытеснит…
-Постой! Говоришь объем неравный?
Матер мой мошенник явный!
За фальшивую корону от ответит по закону!
А ты за разгадку получишь дары.
Слайд 93
Теорема Пифагора
Если дан нам треугольник
И при том с
прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в
квадрат возводим,Сумму степеней находим –
И таким простым путем
К результату мы придем.
И. Дырченко