трапеции
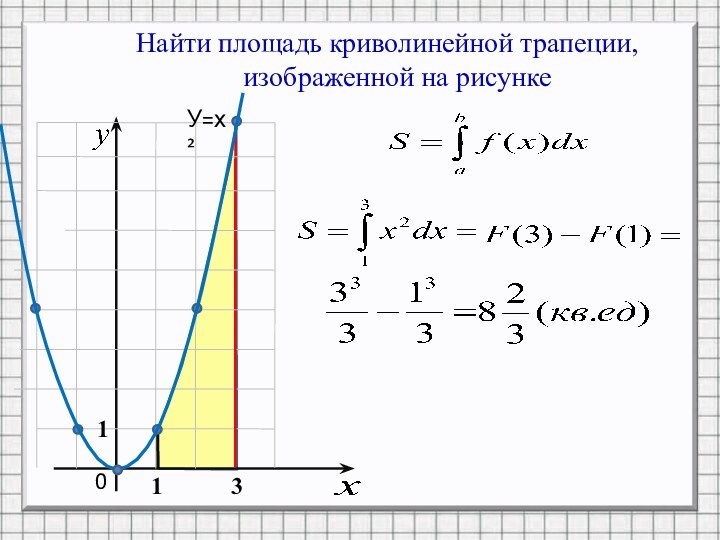
Криволинейной трапецией называется фигура,
ограниченная графиком непрерывной и не
меняющейна отрезке [а;b] знака функции f(х), прямыми
х=а, x=b и отрезком [а;b].

![Площадь криволинейной трапеции и интеграл Криволинейная трапецияОтрезок [a;b] называют основанием этой криволинейной трапецииКриволинейной трапецией называется фигура, ограниченная](/img/tmb/14/1330891/78d4e1d569777a11e6165de12b1655db-720x.jpg)