Слайд 2
Открытый урок по теме: "Подготовка к экзамену".
План учебного

занятия
Группа: ГК-21 ( 2 курс)
Специальность: «Информационные системы обеспечения градостроительной деятельности»
Раздел
программы: Алгебра и геометрия
Дата:
Дисциплина: Математика
Тема занятия: «Подготовка к экзамену по математике за 2 курс»
Цели занятия:
Образовательные: - обобщить и систематизировать полученные самостоятельно и на уроках знания о математике как науке, предмете,
- углубить знания о практическом применении математики,
- закрепить знания о приемах и методах математических вычислений.
Воспитательные: - воспитать интерес к изучаемой дисциплине,
- воспитать познавательную активность, самостоятельность, упорство в достижении цели.
Развивающие: - развивать умения работать самостоятельно и в группе, самоконтроль и взаимоконтроль,
- развивать техническое и логическое мышление,
- отработать навыки решения задач с использованием формул,
- развить способность самостоятельно использовать на практике полученные знания.
Методы и приемы проведения занятия: - словесный, самостоятельная работа, беседа, коллективная групповая работа, индивидуальные задания.
Оснащенность занятия: - видеопроектор, индивидуальные оценочные листы.
Слайд 4
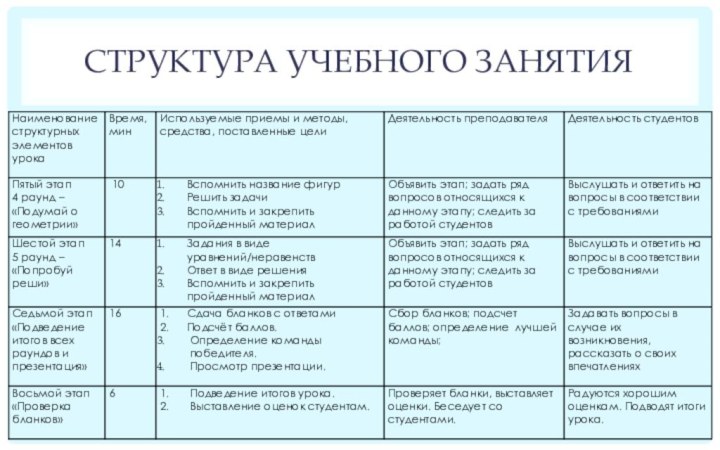
Первый этап
Организационный этап. 6 минут
Проверка явки студентов на
занятие; ведущие раздают бланки для ответов, делят участников на
команды и оглашают правила.
Правила:
1. Задания принимаются последовательности поднятия руки, то
есть проверять задания начинают с первой группы, один из членов
которой первым поднял руку.
2. За попытку списывания заданий с интернета или иных
источников у группы будет изолироваться одна карточка.
3. Каждое задание засчитывается только с условием наличия решения или пояснения (это прописано каждом задании в нижнем углу слайда).
4. Необходимо активное участь каждого члена группы в решении
заданий.
5. За каждый правильный ответ команда получает одну карточку.
Слайд 5
Второй этап
1 раунд - «Узнай формулу» длительность 6
мин
-предоставлено 7 заданий в тестовой форме, за каждый правильный
ответ одной команде засчитывается l балл, на одно задание выделяется 2 минуты.
Задание 1
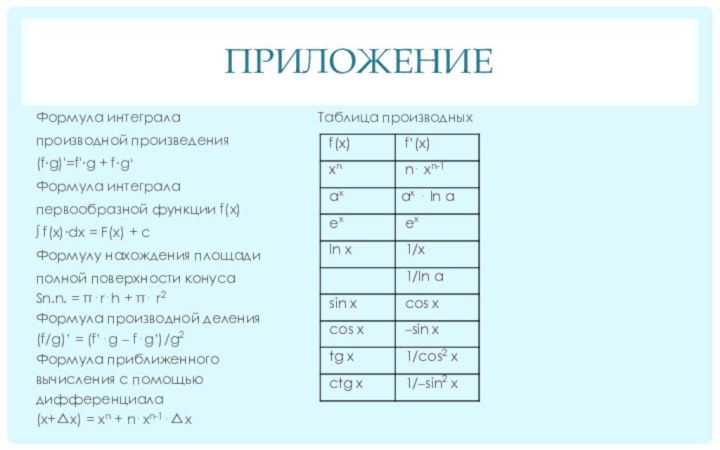
Правила дифференцирования. Найдите формул производной произведения:
а) (f∙g)'=g'∙f - g'∙f
б) (f∙g)'=f'∙g'
в) (f∙g)'=f'∙g + f∙g'
г) (f∙g)'=f'∙g - f∙g' Ответ: в
Слайд 6
Второй этап
Задание 2.
Первообразная. Неопределенный интеграл. Найдите формулу интеграла
первообразной функции f(x):
а) f(x)∙dx = ∫F(x) +
c
б) ∫ f(x)∙dx = F(x) + c
в) ∫ f(x)∙dx = F(x) – с
г) ∫ f(x)∙dx = F(x)∙dy Ответ: б
Задание 3
Производная и дифференциал. Найдите формулу производной и соедините с нужной функцией:
1) sin x a) –sin x д) 1/–sin2 x
2) tg x б) sin x е) 1/cos2 x
3) cos x в) cos x
4) ctg x г) 1/sin2 x Ответ: 1-в, 2-е, 3-а, 4-д
Слайд 7
Второй этап
Задание 4
Найдите формулу нахождения площади полной поверхности
конуса:
а) Sn.n. = π⋅r⋅h + π⋅ r2
б) Sn.n. =
π⋅r⋅h
в) Sn.n. = π⋅r⋅h + (π⋅ r)2
г) Sn.n. = h⋅π⋅r2 Ответ: а
Задание 5
Правила дифференцирования. Найдите формулу производной деления:
а) (f/g)’ = (f’⋅g + f⋅g’)/g2
б) (f/g)’ = (f’⋅g – f⋅g’)/g2
в) (f/g)’ = f’⋅g – f⋅g’
г) (f/g)’ = f⋅g’ – f’⋅g/g2 Ответ: б
Слайд 8
Второй этап
Задание 6
Таблица интегралов. Найдите первообразную и соедините
с интегралом:
1) ∫ dx/x =
а) = -ctg x + c
2) ∫ ax⋅dx = б) = tg x + c
3) ∫ dx/sin2 x = в) = ln x + c
4) ∫ dx/cos2 x = г) = ctg x + c
д) = ln|x|+c
е) = ax /ln a + c Ответ: 1-д, 2-е, 3-а, 4-б
Задание 7
Приближенные вычисления с помощью дифференциала. Найдите правильную формулу:
а) (x+△x) = xn - n⋅xn-1⋅△x
б) (x+△x) = xn + n⋅xn⋅△x
в) (x+△x) = xn + n⋅xn+1⋅△x
г) (x+△x) = xn + n⋅xn-1⋅△x Ответ: г
Слайд 9
третий этап
2 раунд. «Какие слова?» длительность 6 мин
-предоставлено
7 заданий в виде текста, где необходимо вставить пропущенные
слова /словосочетания, за каждый правильный ответ одной команде засчитывается 1 балл, на одно задание выделяется 2 минуты
Задание 1
Теорема умножения вероятностей.
Для зависимых событий: вероятность совместного появления двух зависимых событий равна ________ одного из них на __________ вероятность другого.
Ответ: произведению, условную
Задание 2
Предел функций.
Если старшая степень знаменателя равна старшей степени числителя, то предел функции равен отношению ___________________.
Ответ: коэффициентов при старших степенях
Слайд 10
Третий этап
Задание 3
Промежутки монотонности функции.
Если функция f(x) дифференцируема
(можно найти производную) на интервале (а; b) и f’(x)
– ее производная > 0 на этом интервале, то сама функция ___________ на интервале (а; b).
Ответ: возрастает
Задание 4
Применение производной.
Если при переходе через стационарную точку х(0) производная f’(x) меняет знак, то функция в этой точке имеет _____________.
Ответ: экстремум
Слайд 11
Третий этап
Задание 5
График функции.
Если при переходе через точку
х(0), вторая производная функции y” меняет знак, то сама
функция в точке х(0) имеет ___________.
Ответ: перегиб
Задание 6
Основные понятия комбинаторики.
В комбинаторике подсчитываются варианты исходов испытаний.
Исходы испытаний называются __________.
Ответ: событиями
Задание 7
Пределы функции.
Если старшая степень знаменателя меньше старшей степени числителя, то предел функции равен ____________.
Ответ: бесконечности
Слайд 12
Четвертый этап
3 раунд – «Беспорядок» длительность 6 мин
-
предоставлено 7 заданий, они заключаются в угадывании слова, буквы
которого расположены в беспорядочной последовательности, за каждый правильный ответ одной команде засчитывается 1 балл, на одно задание выделяется 2 минута
Задание 1 Задание 2
Составьте слово: Составьте слово:
и р о я г о м н р т и е т ф ц е и д р е ф а и л н
Ответ: тригонометрия Ответ: дифференциал
Задание 3
Составьте слово:
ь и л а р о н ц о т а ц с ь
Ответ: рациональность
Слайд 13
Четвертый этап
Задание 4 Задание 5
Составьте слово: Составьте слово:
р а т
и м и а к ф е е и р
е п е с н е ч е
Ответ: арифметика Ответ: пересечение
Задание 6 Задание 7
Составьте слово: Составьте слово:
ф о г л и м р а я р о п в а з и д о н и
Ответ: логарифм Ответ: производная
Слайд 14
Пятый этап
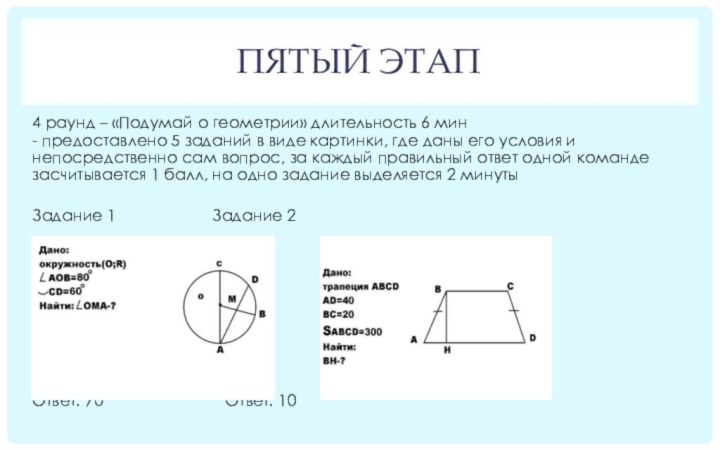
4 раунд – «Подумай о геометрии» длительность
6 мин
- предоставлено 5 заданий в виде картинки, где
даны его условия и непосредственно сам вопрос, за каждый правильный ответ одной команде засчитывается 1 балл, на одно задание выделяется 2 минуты
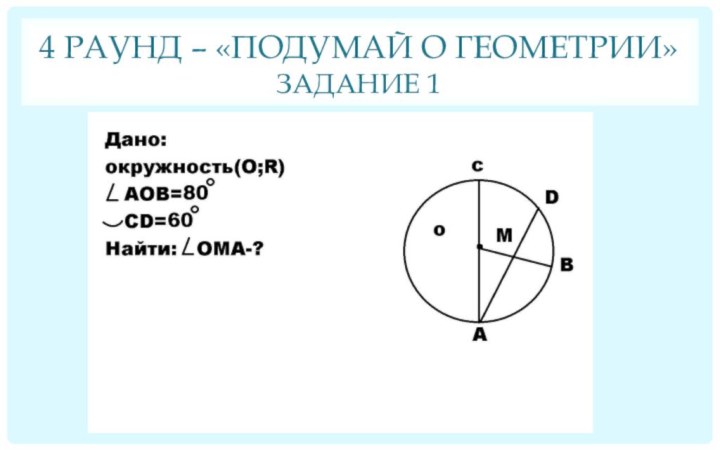
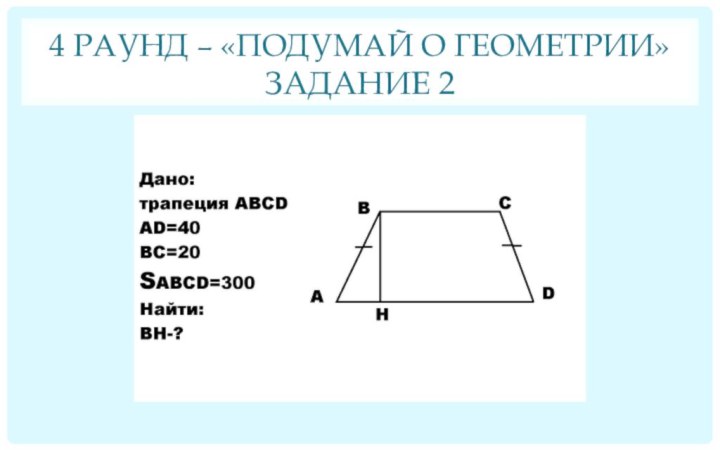
Задание 1 Задание 2
Ответ: 70° Ответ: 10
Слайд 15
Пятый этап
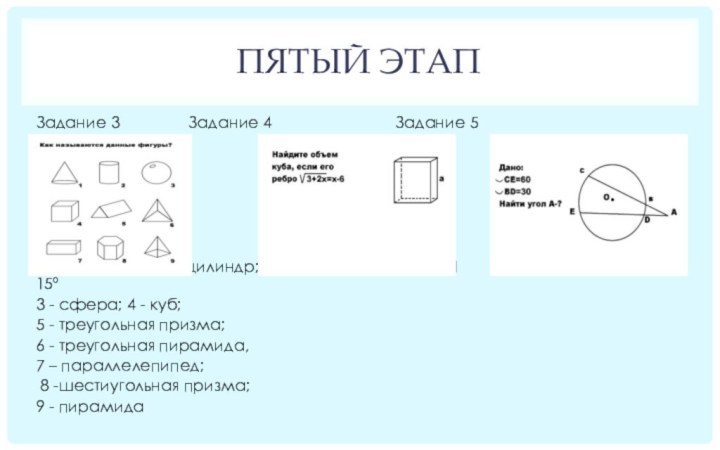
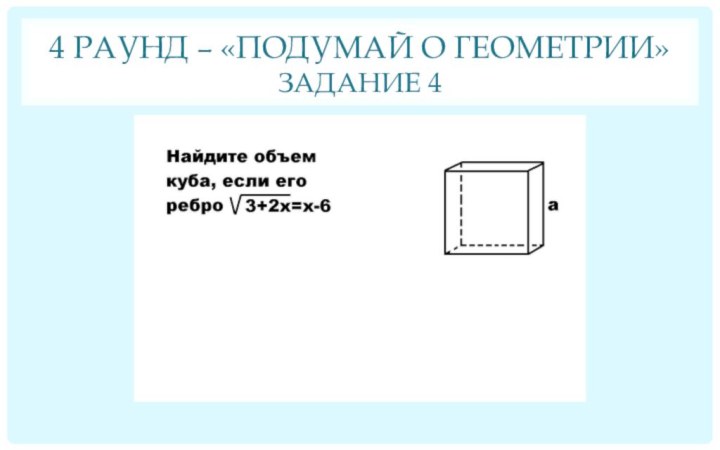
Задание 3 Задание 4
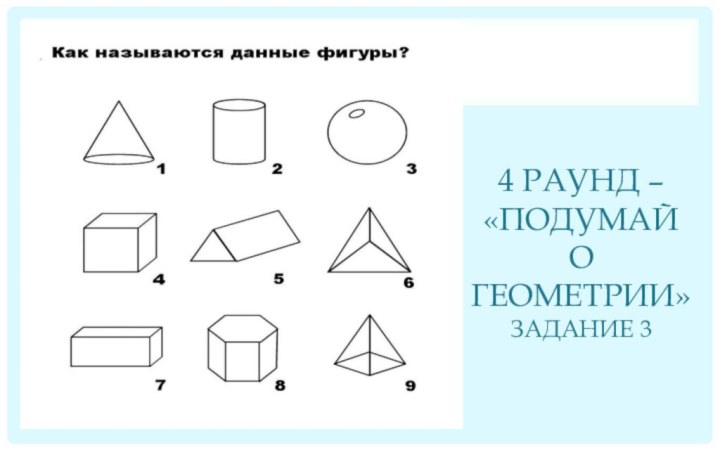
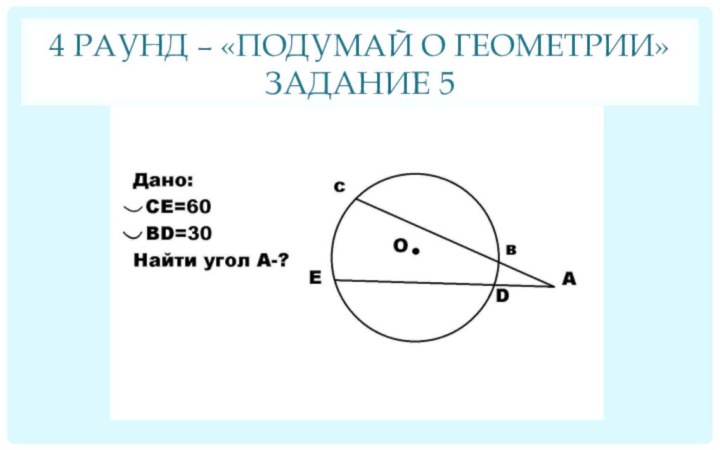
Задание 5
\
Ответ:
1- конус; 2 - цилиндр; Ответ: а = 11; V = 1331 Ответ: 15°
3 - сфера; 4 - куб;
5 - треугольная призма;
6 - треугольная пирамида,
7 – параллелепипед;
8 -шестиугольная призма;
9 - пирамида
Слайд 16
Шестой этап
5 раунд – «Попробуй реши» длительность 24
мин
- предоставлено 7 заданий в виде уравнений/неравенств, ответ на
которые нужно преподнести с решением, за каждый правильный ответ одной команде засчитывается 1 балл, на одно задание выделяется 3 минуты
Задание 1
Формула полной вероятности.
На склад поступили детали с 3 станков. На 1 станке изготовлено 40% всех деталей, на 2 – 35%, на 3 – 25%, причем на 1 станке изготовлено 90% деталей первого сорта, на 2 станке 80%, на 3 станке 70%. Какова вероятность, что взятая деталь будет первого сорта?
Ответ: 0,815
Слайд 19
Седьмой этап
«Подведение общих итогов»
Проведем подсчет итогов каждого раунда
и выявим команду победителей, у которой большее количество набранных
баллов в процессе решения заданий.
Каждой команде необходимо сдать количество бланков с ответами в соответствии с количеством участников данной команды. В дальнейшем преподаватель проверит и выставит оценки каждому участнику.
«Презентация»
Во время подведения итогов студентам будет представлена презентация на тему: «Роль игр в обучении». После просмотра студенты могут высказать свои эмоции и мнение.
Слайд 20
ХОД УРОКА
Учитель: Здравствуйте, студенты. Садитесь, пожалуйста.
Староста: Отсутствуют следующие
студенты ……………….
Учитель: Тема сегодняшнего занятия "Подготовка к экзамену". Этот
урок обобщает и систематизирует полученные знания по всем пройденным темам. Сегодня мы будем решать задачи в команде. Сейчас вы разделитесь на команды и получите бланки для ответов. В конце урока я соберу бланки и каждый из вас получит оценку.
Ведущая (Ксения): *раздает бланки для ответов*
Студенты: *делятся на команды и подписывают бланки*
Ведущая (Виктория): Здравствуйте, ребята! Сейчас я вам расскажу о правилах! *оглашает правила* Итак, первый раунд! *задает вопросы 1 раунда*
Студенты: *отвечают в соответствии с требованиями, оглашенными в правилах*
Ведущая (Ксения): *дает карточки за правильные ответы*
Учитель: *наблюдает за работой студентов*
Слайд 21
Ход УРОКА
Ведущая (Виктория): Приступим ко второму раунду! *задает
вопросы 2 раунда*
Студенты: *отвечают в соответствии с требованиями оглашенными
в правилах*
Ведущая (Ксения): *дает карточки за правильные ответы*
Учитель: *наблюдает за работой студента*
Ведущая (Марина): Приступим к третьему раунду! *задает вопросы 3 раунда*
Студенты: *отвечают в соответствии с требованиями оглашенными в правилах*
Ведущая (Ксения): *дает карточки за правильные ответы*
Учитель: *наблюдает за работой студента*
Ведущая (Марина): Приступим к 4 раунду! *задает вопросы 4 раунда*
Ведущая (Ксения): *дает карточки за правильные ответы*
Учитель: *наблюдает за работой студента*
Ведущая (Виктория): Приступим к последнему пятому раунду! *задает вопросы 5раунда*
Слайд 22
Ход УРОКА
Студенты: *отвечают в соответствии с требованиями оглашенными
в правилах*
Ведущая (Ксения): *дает карточки за правильные ответы*
Учитель: *наблюдает
за работой студента*
Ведущая (Ксения): *собирает бланки с ответами, подсчитывает правильные ответы каждой команды, выявляет команду победителя*
Учитель: Победителем становится …… команда! Молодцы ребята! Как думаете, стоит ли проводить подобные игры чаще? Они помогают усвоить материал?
Студенты: *высказывают свое мнение, делятся впечатлениями, задают вопросы*
Учитель: *отвечает на вопросы, делится своим впечатлением, ведет обсуждение урока*
Студенты: *обсуждают урок*
Учитель: *проверяет бланки с ответами, оглашает оценки*
Студенты: *радуются и благодарят за урок*
Слайд 23
Преподаватель: Винель Елена
Юльяновна
ГРУППА: ГК-21
Калининград
2019
Презентация открытого урока по математике
Слайд 24
Правила
1. Задания принимаются в последовательности поднятия руки, то
есть
проверять задания начинают
с первой группы, один из членов
которой первым поднял руку.
2. За попытку списывания заданий с интернета или иных источников у
группы будет изолироваться одна карточка.
3. Каждое задание засчитывается только с условием наличия решения
или пояснения (это прописано в каждом задании в нижнем углу
слайда).
4. Необходимо активное участие каждого члена группы в решении
заданий.
Слайд 25
ХОД ЗАНЯТИЯ
1 раунд – «Узнай формулу» длительность 6
мин
- предоставлено 7 заданий в тестовой форме, за каждый
правильный ответ одной команде засчитывается 1 балл, на одно задание выделяется не более 1 минуты
2 раунд – «Какие слова?» длительность 6 мин
- предоставлено 7 заданий в виде текста, где необходимо вставить пропущенные слова/словосочетания, за каждый правильный ответ одной команде засчитывается 1 балл, на одно задание выделяется не более 1 минуты
Слайд 26
Ход занятия
3 раунд – «Беспорядок» длительность 6 мин
-
предоставлено 7 заданий, они заключаются в угадывании слова, буквы
которого расположены в беспорядочной последовательности, за каждый правильный ответ одной команде засчитывается 1 балл, на одно задание выделяется не более 1 минуты
4 раунд – «Подумай о геометрии» длительность 14 мин
- предоставлено 5 заданий в виде картинки, где даны его условия и непосредственно сам вопрос, за каждый правильный ответ одной команде засчитывается 1 балл, на одно задание выделяется около 2 минут
Слайд 27
Ход занятия
5 раунд – «Попробуй реши» длительность 24
мин
- предоставлено 7 заданий в виде
уравнений/неравенств, ответ на которые нужно
преподнести с решением , за каждый правильный
ответ одной команде засчитывается 1 балл, на одно
задание выделяется 3 минуты
Ответы предоставляются поднятием руки, в конце каждого раунда осуществляется подсчет общих баллов всех команд и выделяется команда с наибольшим количеством баллов.
Слайд 28
1 раунд – «Узнай формулу»
1. Правила
дифференцирования. Найдите формулу производной произведения:
а) (f ⋅ g)’ =
g’⋅ f – g’ ⋅ f
б) (f ⋅ g)’ = f’ ⋅ g’
в) (f ⋅ g)’ = f’⋅ g + f ⋅ g’
г) (f ⋅ g)’ = f’⋅ g – f ⋅ g’
Ответ предоставляется поднятием руки
Слайд 29
1 раунд – «Узнай формулу»
2. Первообразная. Неопределенный
интеграл. Найдите формулу интеграла первообразной функции f(x):
а) f(x) dx
= ∫F(x) + c
б) ∫ f(x) dx = F(x) + c
в) ∫ f(x) dx = F(x) – с
г) ∫ f(x) dx = F(x)⋅dy
Ответ предоставляется поднятием руки
Слайд 30
1 раунд – «Узнай формулу»
3. Производная и
дифференциал. Найдите формулу производной и соедините с нужной функцией:
1)
sin x a) –sin x д) 1/–sin2 x
2) tg x б) sin x е) 1/cos2 x
3) cos x в) cos x
4) ctg x г) 1/sin2 x
Ответ предоставляется поднятием руки
Слайд 31
1 раунд – «Узнай формулу»
4. Найдите формулу
нахождения площади полной поверхности конуса:
а) Sn.n. = π⋅r⋅h +
π⋅ r2
б) Sn.n. = π⋅r⋅h
в) Sn.n. = π⋅r⋅h + (π⋅ r)2
г) Sn.n. = h⋅π⋅r2
Ответ предоставляется поднятием руки
Слайд 32
1 раунд – «Узнай формулу»
5. Правила дифференцирования.
Найдите формулу производной деления:
а) (f/g)’ = (f’⋅g + f⋅g’)/g2
б) (f/g)’ = (f’⋅g – f⋅g’)/g2
в) (f/g)’ = f’⋅g – f⋅g’
г) (f/g)’ = f⋅g’ – f’⋅g/g2
Ответ предоставляется поднятием руки
Слайд 33
1 раунд – «Узнай формулу»
6. Таблица интегралов.
Найдите первообразную и соедините с интегралом:
1) ∫ dx/x =
а) = -ctg x + c д) = ln|x|+c
2) ∫ ax⋅dx = б) = tg x + c е) = ax /ln a + c
3) ∫ dx/sin2 x = в) = ln x + c
4) ∫ dx/cos2 x = г) = ctg x + c
Ответ предоставляется поднятием руки
Слайд 34
1 раунд – «Узнай формулу»
7. Приближенные вычисления
с помощью дифференциала. Найдите правильную формулу:
а) (x+△x) = xn
- n⋅xn-1⋅△x
б) (x+△x) = xn + n⋅xn⋅△x
в) (x+△x) = xn + n⋅xn+1⋅△x
г) (x+△x) = xn + n⋅xn-1⋅△x
Ответ предоставляется поднятием руки
Слайд 35
2 раунд – «Какие слова?»
1. Теорема умножения
вероятностей.
Для зависимых событий: вероятность совместного появления двух зависимых событий
равна _____________ одного из них на _______________ вероятность другого.
Ответ предоставляется поднятием руки
Слайд 36
2 раунд – «Какие слова?»
2. Предел функций.
Если
старшая степень знаменателя равна старшей степени числителя, то предел
функции равен отношению ___________________.
Ответ предоставляется поднятием руки
Слайд 37
2 раунд – «Какие слова?»
3. Промежутки монотонности
функции.
Если функция f(x) дифференцируема (можно найти производную) на интервале
(а; b) и f’(x) – ее производная > 0 на этом интервале, то сама функция ___________ на интервале (а; b).
Ответ предоставляется поднятием руки
Слайд 38
2 раунд – «Какие слова?»
4. Применение производной.
Если
при переходе через стационарную точку х(0) производная f’(x) меняет
знак, то функция в этой точке имеет _____________.
Ответ предоставляется поднятием руки
Слайд 39
2 раунд – «Какие слова?»
5. График функции.
Если
при переходе через точку х(0), вторая производная функции y”
меняет знак, то сама функция в точке х(0) имеет ___________.
Ответ предоставляется поднятием руки
Слайд 40
2 раунд – «Какие слова?»
6. Основные понятия
комбинаторики.
В комбинаторике подсчитываются варианты исходов испытаний.
Исходы испытаний называются ___________.
Ответ
предоставляется поднятием руки
Слайд 41
2 раунд – «Какие слова?»
7. Пределы функции.
Если
старшая степень знаменателя меньше старшей степени числителя, то предел
функции равен _______________.
Ответ предоставляется поднятием руки
Слайд 42
3 раунд – «Беспорядок»
1. Составьте слово:
и р
о я г о м н р т и
е
Ответ предоставляется поднятием руки
Слайд 43
3 раунд – «Беспорядок»
2. Составьте слово:
ф ц е
и д р е ф а и л н
Ответ предоставляется поднятием руки
Слайд 44
3 раунд – «Беспорядок»
3. Составьте слово:
ь и
л а р о н ц о т а
ц с ь
Ответ предоставляется поднятием руки
Слайд 45
3 раунд – «Беспорядок»
4. Составьте слово:
р а т
и м и а к ф е
Ответ предоставляется поднятием
руки
Слайд 46
3 раунд – «Беспорядок»
5. Составьте слово:
е и р
е п е с н е ч е
Ответ предоставляется
поднятием руки
Слайд 47
3 раунд – «Беспорядок»
6. Составьте слово:
ф о
г л и м р а
Ответ предоставляется поднятием руки
Слайд 48
3 раунд – «Беспорядок»
7. Составьте слово:
я р
о п в а з и д о н
и
Ответ предоставляется поднятием руки
Слайд 49
4 раунд – «Подумай о геометрии»
Задание 1
Слайд 50
4 раунд – «Подумай о геометрии»
Задание 2
Слайд 51
4 раунд – «Подумай
о геометрии»
Задание 3
Слайд 52
4 раунд – «Подумай о геометрии»
Задание 4
Слайд 53
4 раунд – «Подумай о геометрии»
Задание 5
Слайд 54
5 раунд – «Попробуй реши»
Формула полной вероятности.
На склад
поступили детали с 3 станков. На 1 станке изготовлено
40% всех деталей, на 2 – 35%, на 3 – 25%, причем на 1 станке изготовлено 90% деталей первого сорта, на 2 станке 80%, на 3 станке 70%. Какова вероятность, что взятая деталь будет первого сорта?
Ответ предоставляется только с решением
Слайд 55
5 раунд – «Попробуй реши»
2. Иррациональное уравнение.
Ответ предоставляется
только с решением
Слайд 56
5 раунд – «Попробуй реши»
3. Показательные неравенства.
Ответ засчитывается
только с двумя верными ответами
Слайд 57
5 раунд – «Попробуй реши»
4. Первообразная. Неопределенный интеграл.
Ответ
предоставляется только с решением
Слайд 58
5 раунд – «Попробуй реши»
5. Логарифмическое неравенство.
Ответ предоставляется
только с решением
Слайд 59
5 раунд – «Попробуй реши»
6.Определенный интеграл.
Ответ предоставляется
только с решением
Слайд 60
5 раунд – «Попробуй реши»
7. Предел функции на
бесконечности.
Ответ предоставляется только с решением
Слайд 61
Итоги занятия
Проведем подсчет итогов каждого раунда и выявим
команду победителей, у которой большее количество набранных баллов в
процессе решения заданий.
Каждой команде необходимо сдать количество бланков с ответами в соответствии с количеством участников данной команды. В дальнейшем преподаватель проверит и выставит оценки каждому участнику.
Пока будут подводиться итоги, вашему вниманию будет предоставлена презентация на тему: «Роль игр в обучении».
Слайд 62
Оценочный лист
5 раунд выполняется студентами самостоятельно на оборотной
стороне листа бланка ответов